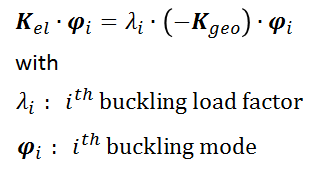Users:General FEM Analysis/Analyses Reference/Buckling
(→General Description) |
(→Defining the eigen problem) |
||
| Line 21: | Line 21: | ||
[[Users:General FEM Analysis/Analyses Reference/Eigenfrequency Analysis|eigenfrequency analysis]]. | [[Users:General FEM Analysis/Analyses Reference/Eigenfrequency Analysis|eigenfrequency analysis]]. | ||
The only difference is that instead of det('''K'''-λ·'''M''')=0 we have to solve det('''K'''''el''+λ·'''K'''''geo'')=0, and so the corresponding eigen problem reads | The only difference is that instead of det('''K'''-λ·'''M''')=0 we have to solve det('''K'''''el''+λ·'''K'''''geo'')=0, and so the corresponding eigen problem reads | ||
| − | [[File:LinBuckling_eigenproblem.png | | + | [[File:LinBuckling_eigenproblem.png | 300px | center | eigen problem of linear buckling analysis ]] |
== Input Parameters == | == Input Parameters == | ||
Revision as of 10:06, 28 April 2011
Contents |
General Description
This analysis performs a linear estimation of the buckling load factor. To this purpose the system stiffness K is considered to consist of two parts, the elastic stiffness Kel, which is well known from the field of linear static analysis, and the geometric stiffness part Kgeo which is associated to the current state of stress. The complete stiffness can be determined as K = Kel + Kgeo.
The analysis refers to the load factor γ defined by the user in the input deck. Starting from this load factor a linear dependency of the geometric stiffness with respect to the load augmentation factor λ is assumed, and so the critical load augmentation factor where buckling occurs can be estimated by demanding singularity of the complete stiffness (linearized w.r.t. λ):
As the linear dependency of Kgeo w.r.t. λ is a simplifying assumption, the estimated total load carrying factor γ·λ is the more exact the closer λ is to 1.
Defining the eigen problem
The equation shown above leads to the solution of an eigen problem similar to the one known from eigenfrequency analysis. The only difference is that instead of det(K-λ·M)=0 we have to solve det(Kel+λ·Kgeo)=0, and so the corresponding eigen problem reads
Input Parameters
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| SOLVER | PC-SOLVER int | Linking to a linear solver (direct or iterative) |
| OUTPUT | PC-OUT int | Linking to output objects (specifies the type of output format, e.g. GiD) |
| COMPCASE | LD-COM int | Linking to computation case objects which specify the boundary conditions (loading and supports) |
| DOMAIN | EL-DOMAIN int | Linking to the domain the analysis should work on |
Example of a Complete Input Block
PC-ANALYSIS 1: STA_GEO_LIN SOLVER = PC-SOLVER 5 OUTPUT = PC-OUT 1 COMPCASE = LD-COM 1,2,3 DOMAIN = EL-DOMAIN 1
A Full Example
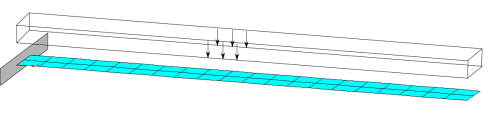
The following example describes a simple cantilever problem discretized by SHELL8 elements. The respective input file can be found here:
The problem computes three computation cases (dead load, snow load and pressure load). The boundary conditions are visualized by the figure below.
The basic goal of each linear static analysis is the computation of the displacement field. For load case 1 this result is depicted in the figure below, whereas the deformation in z-direction is additionally visualized by the color plot.
It can be seen that the support region does not show any deformation whereas the tip region deforms by a value of 8.76.
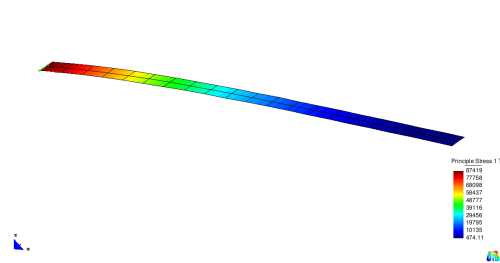
Often the stress distribution is visualized by color plots. Shell structures require the specification of the layer on which the stresses are computed. The picture below shows the first principle stress on the top of the cantilever.
It can be seen that the stresses show maximum values at the support region of the cantilever. At the tip they are nearly zero. In contrast to analytical results the stresses are not exactly zero in numerical models. The reason is the stress computation at the Gauss points. These points are situated inside the elements and not exactly at the tip of the cantilever.
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |