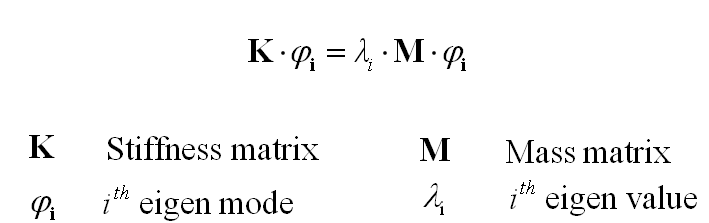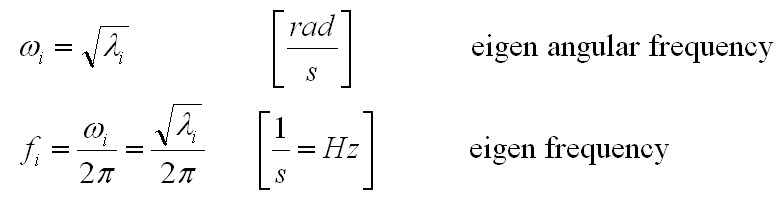Users:General FEM Analysis/Analyses Reference/Eigenfrequency Analysis
Contents |
General Description
This analysis is intended for the solution of dynamic eigenvalue problems. It is suitable for analyzing the vibration characteristics of structures and to determine their eigenfrequencies.
Structure of governing equation
A dynamic eigenvalue problem is defined by the equation
with the unknown eigen mode φ and the corresponding eigen value λ, which is unknown, too. The equation shown above is a classical eigenvalue problem defined by the sparse matrices K and M, which can be solved by an eigenvalue solver.
The equation shows that the problem does not depend on external loads. This underlines that the eigenfrequency analysis refers to the homogeneous solution of the underlying PDE only.
Inclusion of External Loads
Alternatively, a dynamic eigenvalue analysis of a structure under external loads, e.g. self weight, could be performed by definition of external loads and triggering of the "INITIAL_STATIC_CALCULATION" flag in the PC-ANALYSIS section. Such an analysis considers the geometrical nonlinearities and stiffness variations that arise from the external loading by performing a priori geometrically nonlinear static analysis. By doing so, the stiffness matrix that is used for the eigenfrequency analysis is updated with the nonlinear stiffness of the structure. A solver for this static step necessitates the definition of an additional solver. An example input block is presented in the "Input Parameters" section.
Relation between Eigenvalue and Eigenfrequency
The equation above refers to the eigenvalue of the dynamic eigenvalue problem defined by the system matrices. What the user usually is interested in is the eigenfrequeny of the system. The relation between these values is the following:
Input Parameters
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| PC-ANALYSIS | int : EIGENFREQUENCY | Analysis ID |
| EIGEN_SOLVER | PC-SOLVER int | Linking to an eigen solver |
| OUTPUT | PC-OUT int | Linking to output objects (specifies the type of output format, e.g. GiD) |
| COMPCASE | LD-COM int | Linking to computation case objects which specify the boundary conditions (supports only!) |
| DOMAIN | EL-DOMAIN int | Linking to the domain the analysis should work on |
| NUM_ROOT | int | Number of eigen values to be computed |
| MASS_LUMPED | 0, 1 | indicates if mass matrix is lumped (1) or not (0) |
Example of a Complete Input Block
PC-ANALYSIS 1: EIGENFREQUENCY EIGEN_SOLVER = PC-SOLVER 1 OUTPUT = PC-OUT 1 COMPCASE = LD-COM 1 DOMAIN = EL-DOMAIN 1 NUM_ROOT = 4 MASS_LUMPED = 0
Example of a Complete Input Block with consideration of External Loads
PC-ANALYSIS 1: EIGENFREQUENCY EIGEN_SOLVER = PC-SOLVER 1 LINEAR_SOLVER = PC-SOLVER 2 OUTPUT = PC-OUT 1 COMPCASE = LD-COM 1 DOMAIN = EL-DOMAIN 1 NUM_ROOT = 4 MASS_LUMPED = 0 INITIAL_STATIC_CALCULATION=TRUE INITIAL_LOAD_STEPS = 1 MAX_ITER_EQUILIBRIUM = 100 EQUILIBRIUM_ACCURACY = 1e-12
Examples
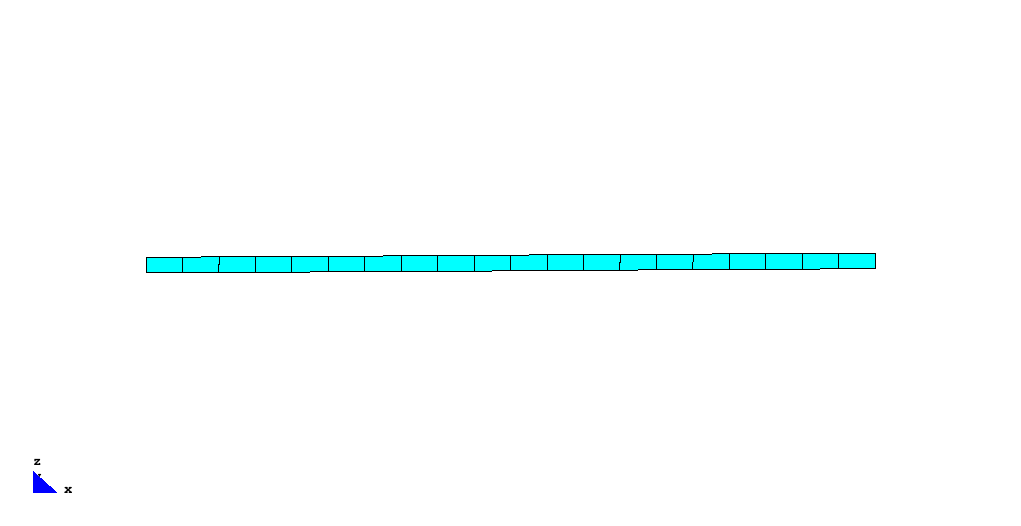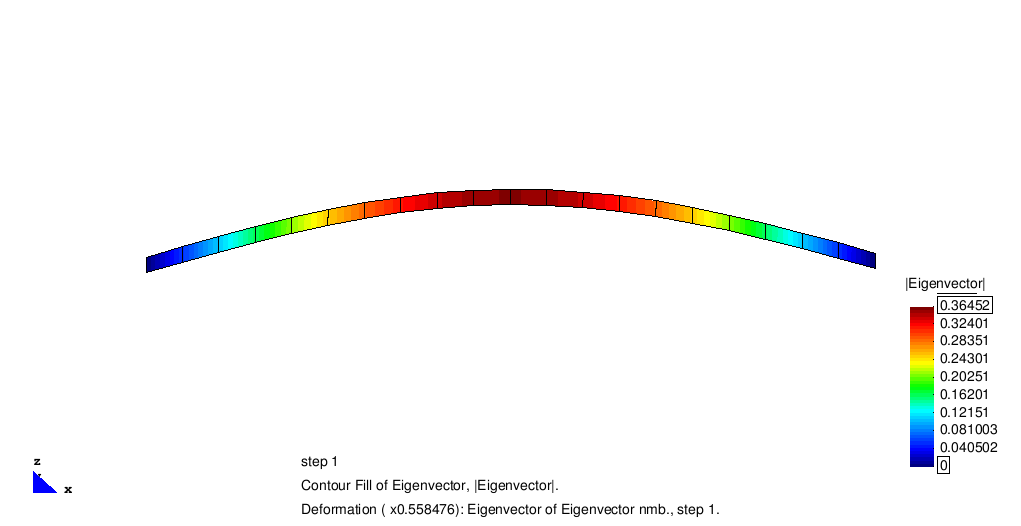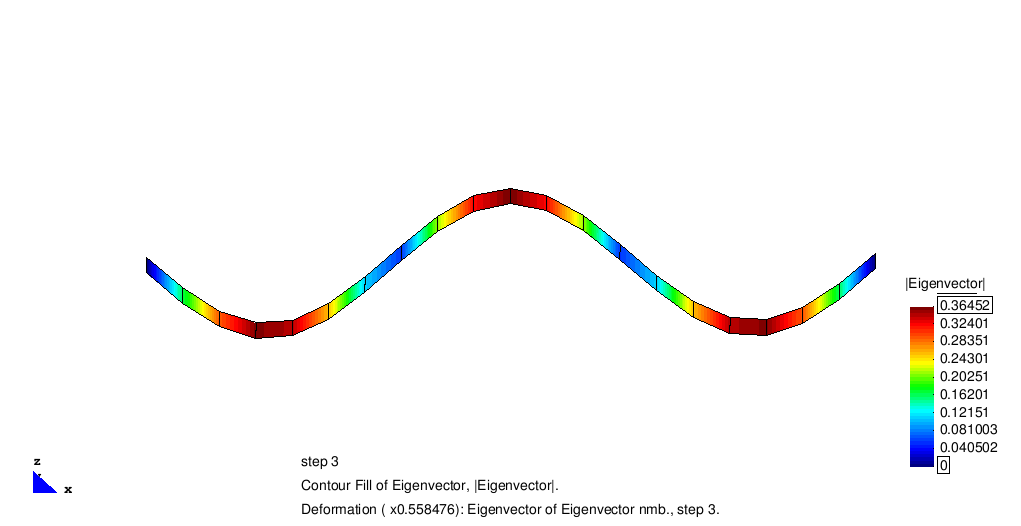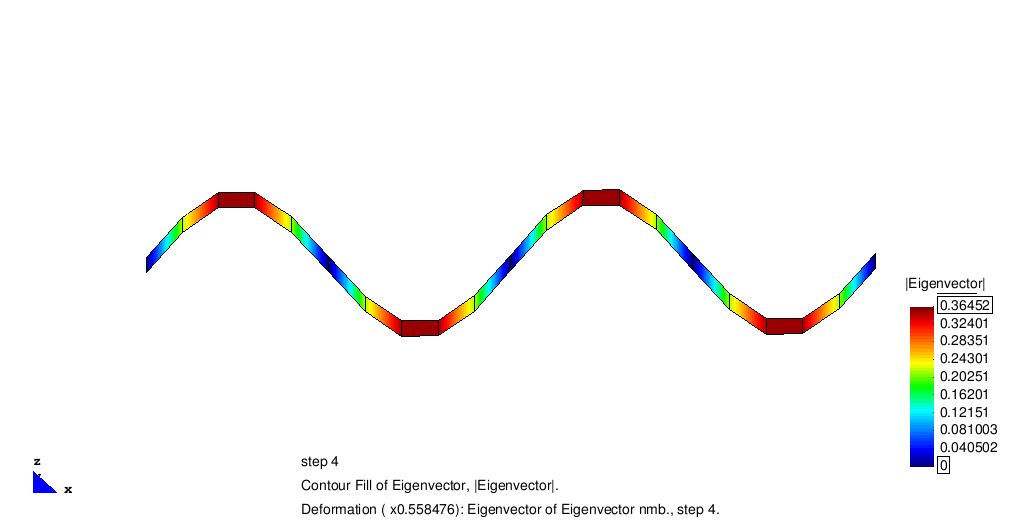
Example of shell-discretized beam
The standard benchmark for eigen dynamics is a fixed supported beam modeled by SHELL8-elements. Due to its mass, stiffness and geometry the first four eigen frequencies can be computed analytically to
1st: 5.878 Hz
2nd: 23.513 Hz
3rd: 52.904 Hz
4th: 94.052 Hz
The corresponding Carat output reads
##########################################
### Results of eigenfrequency analysis ###
##########################################
Number of eigenfrequencies to compute: 4
Number | Eigenfrequency | Eigenvalue
-------------------------------------------------------
1 5.896354e+00 1.372546e+03
2 2.380388e+01 2.236945e+04
3 5.439391e+01 1.168047e+05
4 9.884036e+01 3.856811e+05
-------------------------------------------------------
Eigenfrequency Analysis finished!
The finite element computation approximates the first eigenfrequency with an error of only 0.3%. The fourth eigenfrequency is still approximated within a tolerance of 5%.
The full imput file belonging to this example can be found in the current Carat revision:
- ..\examples\benchmark_examples\analyses\eigenfrequency_shell8_beam\shell8_beam_eigenfreq.dat
The following animation illustrates the system and the corresponding eigen vectors.
Benchmark examples
- eigenfrequency of a single-span beam discretized by (SHELL8)-elements: ..\examples\benchmark_examples\analyses\eigenfrequency_shell8_beam\shell8_beam_eigenfreq.dat
- eigenfrequency of a plate discretized by (SHELL8)-elements: ..\examples\benchmark_examples\analyses\eigenvalue_shell8_plate\cbm_eigenvalue_shell8_plate.dat
- eigenfrequency of cable discretized by (TRUSS1)-elements: ..\examples\benchmark_examples\analyses\eigenvalue_truss1_I\cbm_vib_row_50_elm.txt
- eigenfrequency of a flat plate discretized by (MEMBRANE1)-elements with prestress: ..\examples\benchmark_examples\analyses\eigenvalue_membrane1_I\cbm_Dynamic_Membrane_200_elm.txt
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |