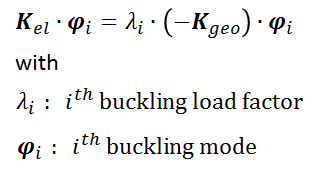Users:General FEM Analysis/Analyses Reference/Buckling
(→A Full Example) |
(→A Full Example) |
||
| Line 76: | Line 76: | ||
The following example describes a rod buckling problem. A built in rod of length 2 is loaded in normal direction by a pressure force of 1, the croess section's bending stiffness is equal to 1750. The buckling load according to Euler's formula computes to | The following example describes a rod buckling problem. A built in rod of length 2 is loaded in normal direction by a pressure force of 1, the croess section's bending stiffness is equal to 1750. The buckling load according to Euler's formula computes to | ||
| − | |||
[[File:LinBuckling_euler.png|200px]] | [[File:LinBuckling_euler.png|200px]] | ||
Revision as of 11:21, 28 April 2011
Contents |
General Description
This analysis performs a linear estimation of the buckling load factor. To this purpose the system stiffness K is considered to consist of two parts, the elastic stiffness Kel, which is well known from the field of linear static analysis, and the geometric stiffness part Kgeo which is associated to the current state of stress. The complete stiffness can be determined as K = Kel + Kgeo.
The analysis refers to the load factor γ defined by the user in the input deck. Starting from this load factor a linear dependency of the geometric stiffness with respect to the load augmentation factor λ is assumed, and so the critical load augmentation factor where buckling occurs can be estimated by demanding singularity of the complete stiffness (linearized w.r.t. λ):
As the linear dependency of Kgeo w.r.t. λ is a simplifying assumption, the estimated total load carrying factor γ·λ is the more exact the closer λ is to 1.
Defining the eigen problem
The equation shown above leads to the solution of an eigen problem similar to the one known from eigenfrequency analysis. The only difference is that instead of det(K-λ·M)=0 we have to solve det(Kel+λ·Kgeo)=0, and so the corresponding eigen problem reads
Input Parameters
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| EIGEN_SOLVER | PC-SOLVER int | Linking to an eigen solver |
| LINEAR_SOLVER | PC-SOLVER int | Linking to a linear solver |
| OUTPUT | PC-OUT int | Linking to output objects (specifies the type of output format, e.g. GiD) |
| COMPCASE | LD-COM int | Linking to computation case objects which specify the boundary conditions (loading and supports) |
| DOMAIN | EL-DOMAIN int | Linking to the domain the analysis should work on |
| NUM_ROOT | int | Number of buckling modes and load factors to determine |
It should be mentioned that the two solvers used within this analysis (linear and eigen solver) have to be compatible with respect to the used sparse matrix format (e.g. both using a Skyline formate or both working on a TRILINOS Csr matrix):
Example of a Complete Input Block
PC-ANALYSIS 1: LINEAR_BUCKLING EIGEN_SOLVER = PC-SOLVER 1 LINEAR_SOLVER = PC-SOLVER 2 OUTPUT = PC-OUT 1 COMPCASE = LD-COM 1 DOMAIN = EL-DOMAIN 1 NUM_ROOT = 3
A Full Example
The following example describes a rod buckling problem. A built in rod of length 2 is loaded in normal direction by a pressure force of 1, the croess section's bending stiffness is equal to 1750. The buckling load according to Euler's formula computes to
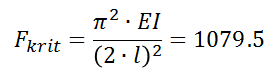
The corresponding input file is available via the following link:
http://www.develop.caratplusplus.de/upload_from_server/benchmark_examples/elements/shell8_quad_lin_canti_I/shell8_canti_2x20_elem_load.dat
The problem computes three computation cases (dead load, snow load and pressure load). The boundary conditions are visualized by the figure below.
The basic goal of each linear static analysis is the computation of the displacement field. For load case 1 this result is depicted in the figure below, whereas the deformation in z-direction is additionally visualized by the color plot.
It can be seen that the support region does not show any deformation whereas the tip region deforms by a value of 8.76.
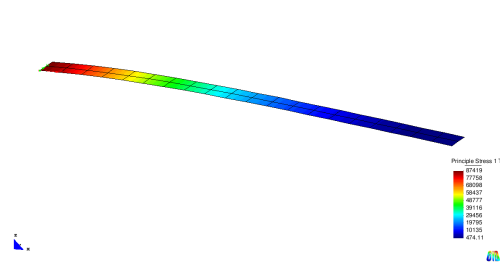
Often the stress distribution is visualized by color plots. Shell structures require the specification of the layer on which the stresses are computed. The picture below shows the first principle stress on the top of the cantilever.
It can be seen that the stresses show maximum values at the support region of the cantilever. At the tip they are nearly zero. In contrast to analytical results the stresses are not exactly zero in numerical models. The reason is the stress computation at the Gauss points. These points are situated inside the elements and not exactly at the tip of the cantilever.
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |