Users:Structural Optimization/Response Functions/Eigenfrequency

Contents 1 General Description 1.1 Short Info 2 Input Parameters 2.1 Example of a Complete Input Block 3 A complete test example 3.1 Model description 3.2 Input File 3.3 Documented Results 4 Theory and Details 5 References

General Description

Short Info

This response function refers to all eigenvalues computed by the eigenvalue analysis. The function itself is a weighted sum of all considered eigenvalues based on the works of Kreisselmeier-Steinhauser ^[1]. The idea of Kreisseleier-Steinhauser was to formulate a optimization objective function that summarizes several response functions and performs an internal weighting according to the relationship of the function values. The current implementation in Carat++ is a formulation that privileges small eigenvalues whereat the weighting can be controlled via the parameter ρ. The higher ρ is set, the more small values are privileged.

This response function is suitable for the maximization of eigenvalues and the corresponding eigenfrequencies.

Input Parameters

Block headline
Parameter	Values, Default(*)	Description
OPT-RESPONSOSE_FCT	int : EIGENFREQUENCY_KS	Function ID and type of response function
Common compulsory parameters
ETA	real	Finite difference disturbance for sensitivity analysis
GRAD	DIRECT, ADJOINT	Method of gradient computation
SA	GLOBAL_FD, SEMI_ANALYTIC, EXACT_SEMI_ANALYTIC, ANALYTIC	Method of derivative computations inside sensitivity analysis
FDA	FOREWARD, CENTRAL, BACKWARD	Method of finite difference approximation (if neccessary for the chosen sensitivity analysis method)
DESVAR	OPT-VAR vector of integers	Design variables that are considered in the sensitivity analysis of this response function
Common optional parameters
WEIGHT	real, 1.0*	The weighting factor for this response function in multi-objective optimization
ANALYSIS	PC-ANALYSIS int	ID of the underlying analysis
Specific parameters
RHO	real	Kreisselmeier-Steinhauser parameter which controls the weighting. Recommended range: 1 to 100. For more details see Theory and details
Common Compulsory Parameters for Constraints
Parameter	Values, Default(*)	Description
REL_LIMIT	real	Relative limit for constraint, depending on the actual value.
ABS_LIMIT	real	Absolute limit for constraint. Only one limit can be defined for a constraint.
CONSTRAINT_TYPE	INEQUALITY_LT, INEQUALITY_GT, EQUALITY	Type of constraint
Common Optional Parameters for Constraints
REL_TOLERANCE	real, 0*	Upper relative limit until which an inactive constraint is concidered as an active one
LAMBDA_ABS_MAX	real, 1/cepsilon*	Upper limit for lagrangian multiplier

Example of a Complete Input Block

This section presents the input sequence for a Kreisselmeier-Steinhauser constraint.

OPT-RESPONSE_FCT 1 : EIGENFREQUENCY_KS
 WEIGHT=1.0 ANALYSIS=PC-ANALYSIS 1 ETA=1e-06
 GRAD=ADJOINT SA=SEMI_ANALYTIC FDA=FOREWARD
! -- response function dependant parameters
 RHO = 1
! -- constraint parameters
 REL_LIMIT = 1.1
 REL_TOLERANCE = 0.1
 CONSTRAINT_TYPE = INEQUALITY_LT
 LAMBDA_ABS_MAX = 20

A complete test example

Model description

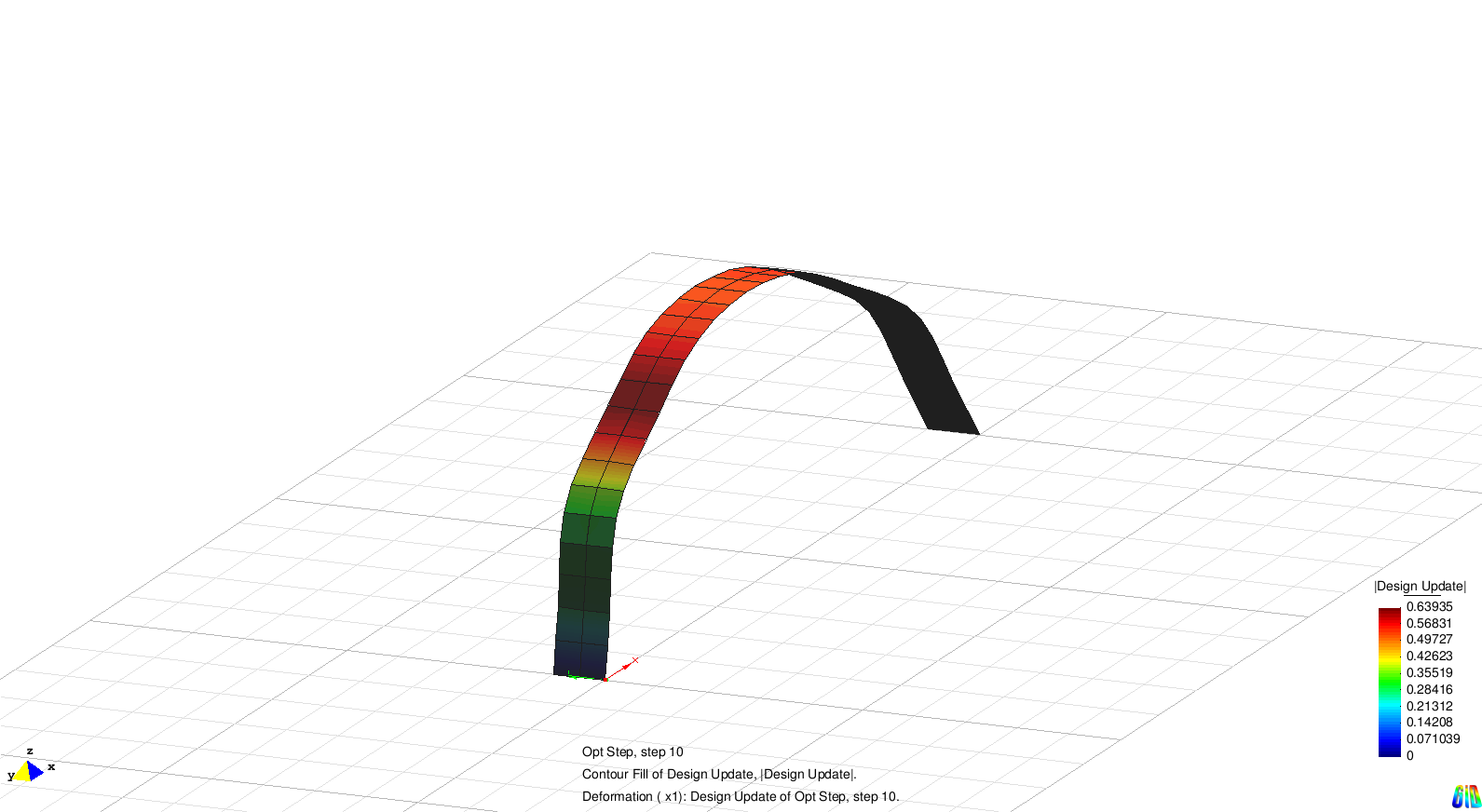
The influence of the paramter ρ will be demonstrated at the example of an arch. The following animation shows the geometry and the first 4 eigenmodes of the system.

This system will be optimized twice, once with ρ=1 and one with ρ=100.

Input File

Here the full input file can be downloaded.

Documented Results

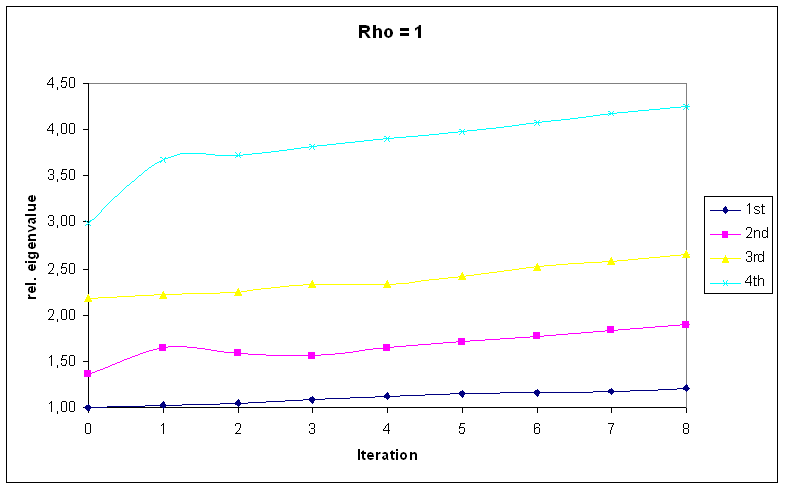
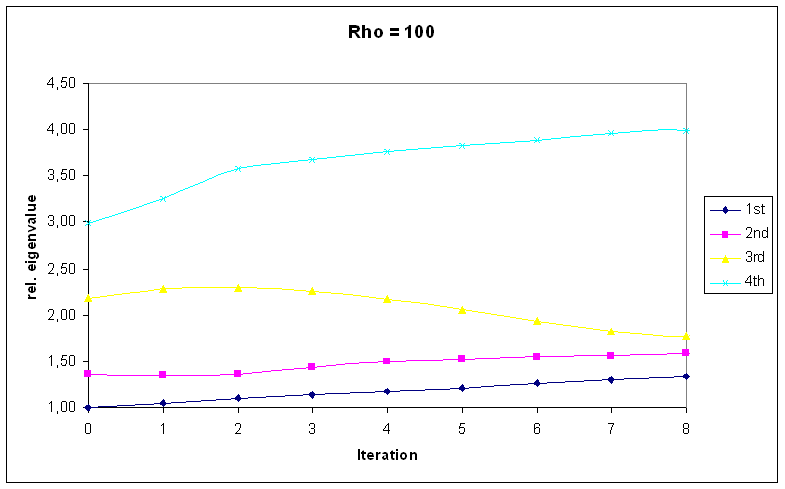
The following figures illustrate the developement of the eigenvalues and the final geometry.

• 

  Developement of eigenvalues for Rho=1

• 

  Developement of eigenvalues for Rho=100

• 

  Final geometry (Rho=1)

• 

  Final geometry (Rho=100)

The first picture shows that for ρ=1 all eigenvalues grow in the process of optimization. Within eight optimization steps they improve by 20 to 40 percent.

In contrast to this, for ρ=100 the first eigenmode is dominant. It increases now 30 percent instead of 20 percent, and at the same time groth of the third and fourth eigenvalue is reduced dramatically. This points out the effect of the control parameter ρ.

Theory and Details

The implementation of the Kreisselmeier-Steinhauser formulation in Carat++ uses the form , where λ is a scaled eigenvalue and s is a shifter. Φ will decrease for increasing eigenvalues, and so a minimization of the Kreisselmeier-Steinhauser function leads to a maximization of the eigenvalues.

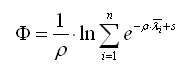
In order to keep the exponential function from overshooting all limits, a scaling is applied to the eigenvalues. To this purpose for each eigenvalue a scaling factor is computed that way that the initial eigenvalues (at the beginning of the optimization) are mapped onto the interval [0.1, 0.5]. Additionally the shifter s is introduced in order to evaluate the exponential function in a region where it is more curved, and so to force the weighing influence of the formulation. The shifter is set to 80. So for a value of ρ=1 the lowest eigenvalue will reach a value of exp( -1*0.1 + 80 ) = 5e34, which is numerically still acceptable.

References

1. ↑ Kreisselmeier, G., and Steinhauser, R., "Systematic Control Design by Optimizing a Vector Performance Index," International Federation of Active Controls Symposium on Computer-Aided Design of Control Systems, Zurich, Switzerland, August 29-31, 1979

Whos here now:   Members 0   Guests 0   Bots & Crawlers 1