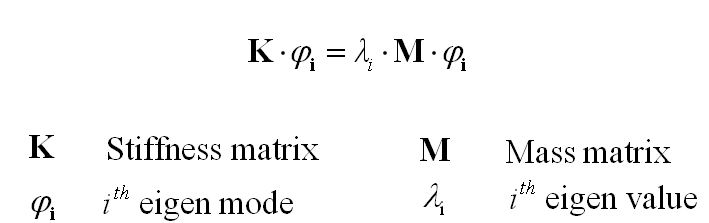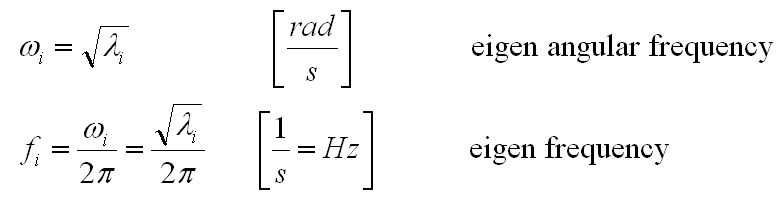Users:General FEM Analysis/Analyses Reference/Eigenfrequency Analysis
Contents |
General Description
This analysis is intended for the solution of eigen dynamic problems. It is suitable for analysing the vibration characteristics of structures and to determine their eigen frequencies.
Structure of governing equation
An eigen dynamics problem is defined by the equation
with the unknown eigen mode φ and the corresponding eigen value λ, which is unknown, too. The equation shown above is a classical eigen problem defined by the sparse matrices K and M, which can be solved by an eigen solver.
The equation shows that the problem is not depending on external loads. This underlines that eigen frequency analysis refers to the homogeneous solution of the underlying PDE only.
Inclusion of External Loads
Alternatively, an eigen dynamics analysis of a structure under external loads, e.g. self weight, could be performed by definition of external loads and triggering of the "INITIAL_STATIC_CALCULATION" flag in the PC-ANALYSIS section. Such an analysis considers the loading by making use of the geometric stiffness contribution by performing an a priori static analysis. A solver for this static step necessitates a definition of an additional solver. An example input block is presented in the "Input Parameters" section
Relation between Eigenvalue and Eigenfrequency
The equation above refers to the eigen value of the eigen problem defined by the system matrices. What the user usually is interested in is the eigen frequeny of the system. The relation between this values is the following:
Input Parameters
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| PC-ANALYSIS | int : EIGENFREQUENCY | Analysis ID |
| EIGEN_SOLVER | PC-SOLVER int | Linking to an eigen solver |
| OUTPUT | PC-OUT int | Linking to output objects (specifies the type of output format, e.g. GiD) |
| COMPCASE | LD-COM int | Linking to computation case objects which specify the boundary conditions (supports only!) |
| DOMAIN | EL-DOMAIN int | Linking to the domain the analysis should work on |
| NUM_ROOT | int | Number of eigen values to be computed |
| MASS_LUMPED | 0, 1 | indicates if mass matrix is lumped (1) or not (0) |
Example of a Complete Input Block
PC-ANALYSIS 1: EIGENFREQUENCY EIGEN_SOLVER = PC-SOLVER 1 OUTPUT = PC-OUT 1 COMPCASE = LD-COM 1 DOMAIN = EL-DOMAIN 1 NUM_ROOT = 4 MASS_LUMPED = 0
Example
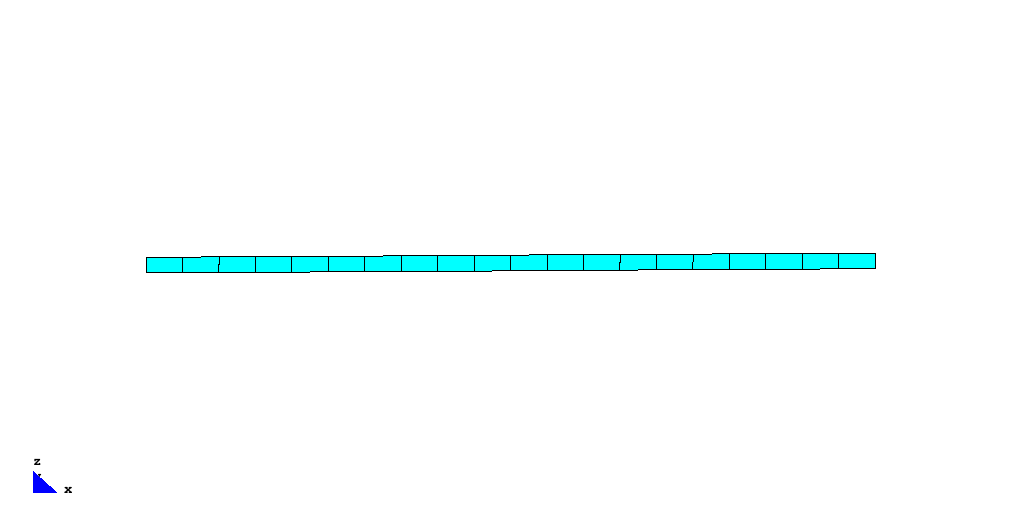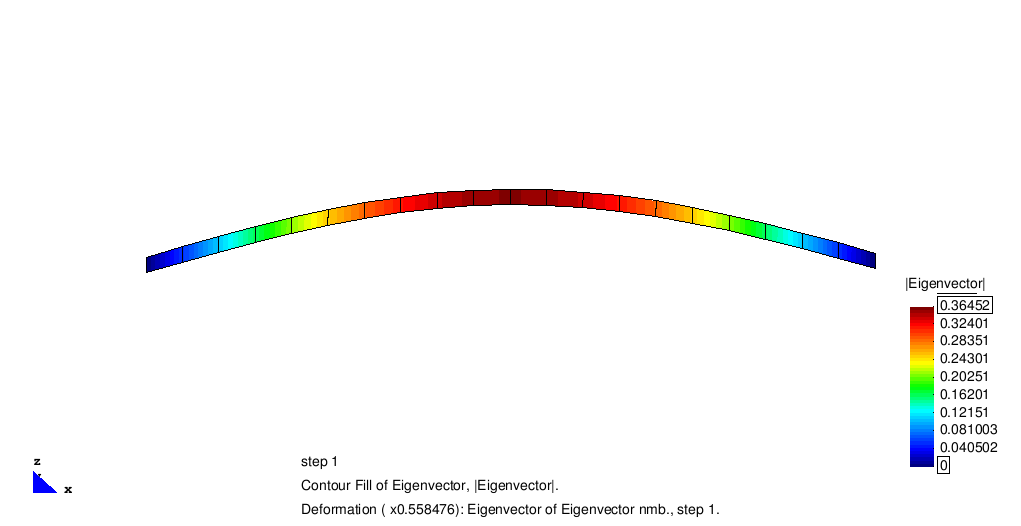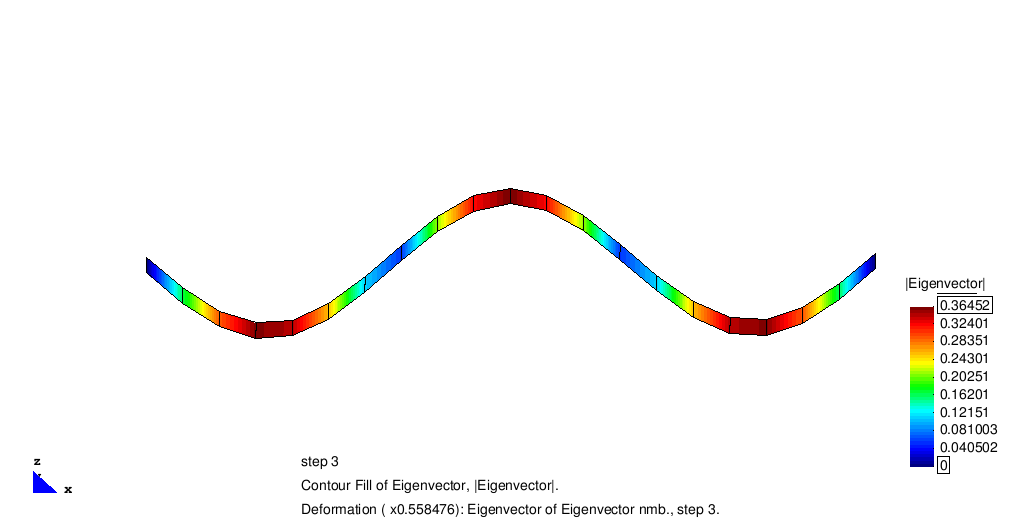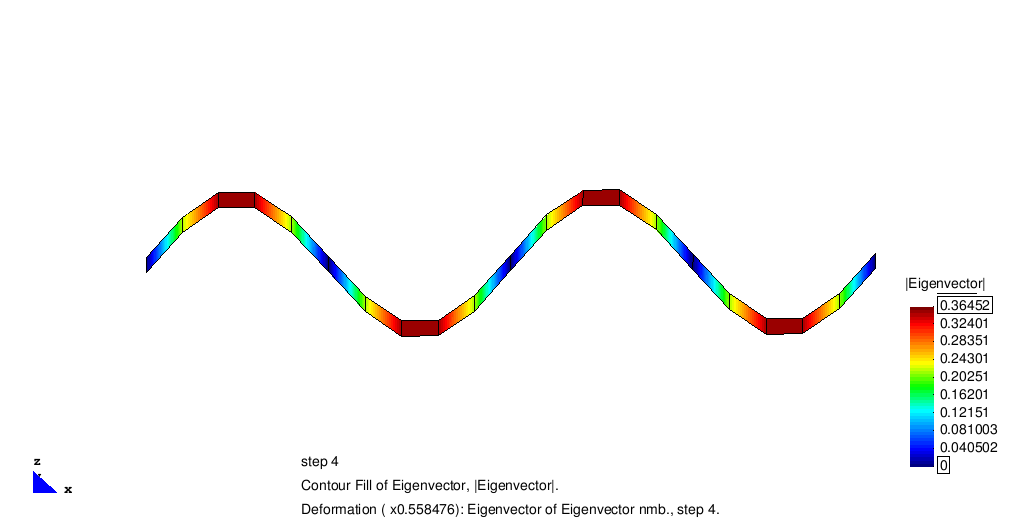
The standard benchmark for eigen dynamics is a fixed supported beam modeled by SHELL8-elements. Due to its mass, stiffness and geometry the first four eigen frequencies can be computed analytically to
1st: 5.878 Hz
2nd: 23.513 Hz
3rd: 52.904 Hz
4th: 94.052 Hz
The related Carat output reads
##########################################
### Results of eigenfrequency analysis ###
##########################################
Number of eigenfrequencies to compute: 4
Number | Eigenfrequency | Eigenvalue
-------------------------------------------------------
1 5.896354e+00 1.372546e+03
2 2.380388e+01 2.236945e+04
3 5.439391e+01 1.168047e+05
4 9.884036e+01 3.856811e+05
-------------------------------------------------------
Eigenfrequency Analysis finished!
The finite element computation approximates the first eigen frequancy with an error of only 0.3%. The fourth eigen frequency is still approximated within a tolerance of 5%.
The full imput file belonging to this example can be found in the current Carat revision under http://www.develop.caratplusplus.de/upload_from_server/benchmark_examples/analyses/eigenfrequency_shell8_beam/shell8_beam_eigenfreq.dat. The following animation illustrates the system and the corresponding eigen vectors.
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |