Users:General FEM Analysis/Elements Reference/Membrane1
| Line 111: | Line 111: | ||
=== Prestress directions on the surface === | === Prestress directions on the surface === | ||
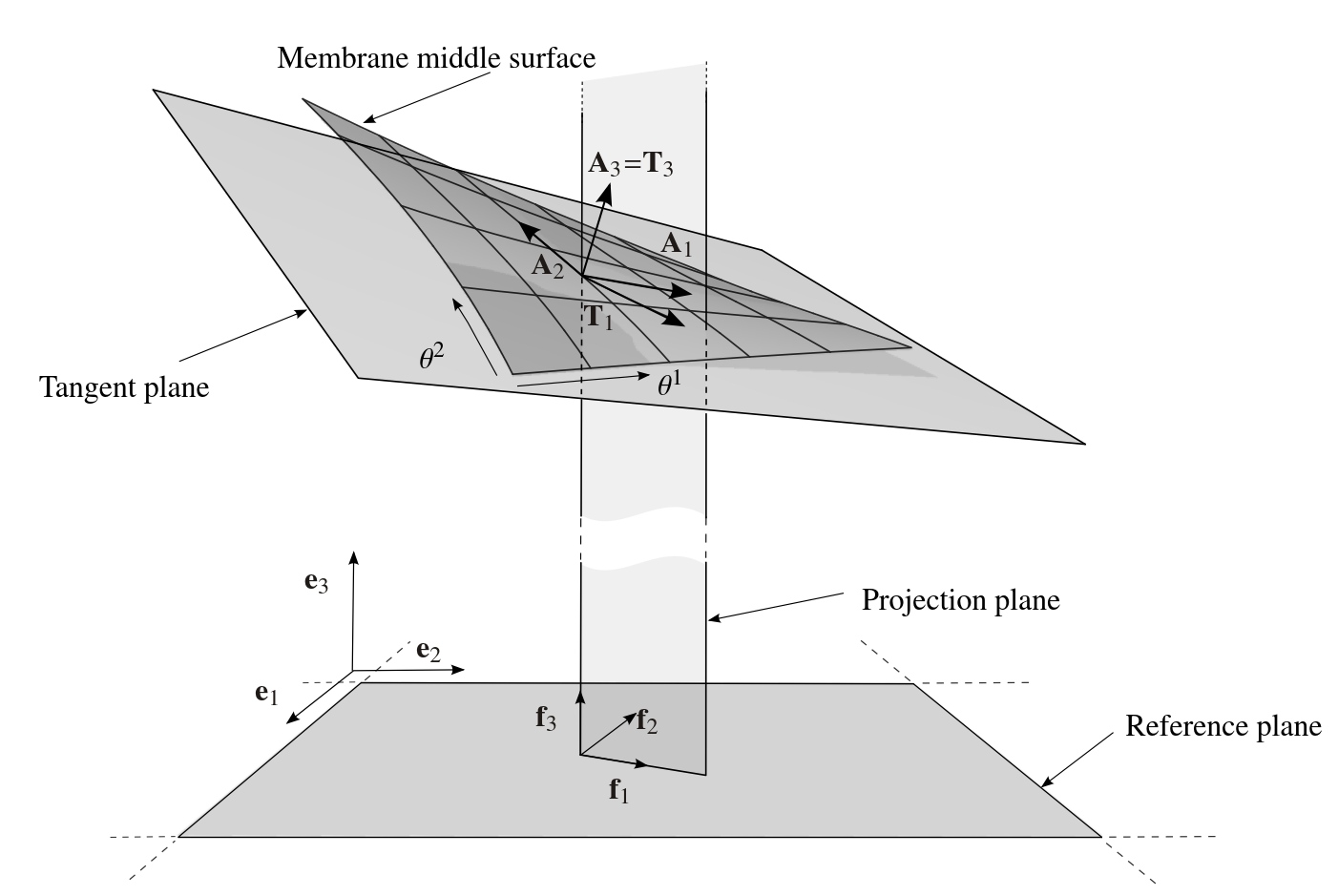
| − | The parameters ''A_X, A_Y, A_Z and B_X, B_Y, B_Z'' are used to define the prestress directions on the surface. In this approach the principal directions of the prestress are defined in a plane area (see figure below). The definition of the area is given by the two vectors '''f'''<sub>1</sub> and '''f'''<sub>2</sub>. The normal vector of the area can be calculated with the cross product of the in plane vectors '''f'''<sub>3</sub>='''f'''<sub>1</sub> x '''f'''<sub>2</sub>. Afterwards the line of intersection '''T'''<sub>1</sub> of the area which is given by '''f'''<sub>1</sub> and '''f'''<sub>3</sub> and the curved surface can be calculated. In this approach '''T'''<sub>1</sub> is interpreted as the first principal direction of the prestress on the curved surface. With the assumption that '''T'''<sub>3</sub> is equal to the surface normal vector '''G'''<sub>3</sub> (not normalized), the second direction of the prestress is calculated as '''T'''<sub>2</sub>='''T'''<sub>1</sub> x '''T'''<sub>3</sub>. W.r.t. the parameters for the input file, only the plane area with the vectors '''f'''<sub>1</sub> and '''f'''<sub>2</sub> has to be defined. Referring to the depicted approach the vector '''A''' defines the vector '''f'''<sub>1</sub> and the vector '''B''' defines the vector '''f'''<sub>2</sub>. | + | The parameters ''A_X, A_Y, A_Z and B_X, B_Y, B_Z'' are used to define the prestress directions on the surface, which is necessary in case of anisotropic prestress conditions. In this approach the principal directions of the prestress are defined in a plane area (see figure below). The definition of the area is given by the two vectors '''f'''<sub>1</sub> and '''f'''<sub>2</sub>. The normal vector of the area can be calculated with the cross product of the in plane vectors '''f'''<sub>3</sub>='''f'''<sub>1</sub> x '''f'''<sub>2</sub>. Afterwards the line of intersection '''T'''<sub>1</sub> of the area which is given by '''f'''<sub>1</sub> and '''f'''<sub>3</sub> and the curved surface can be calculated. In this approach '''T'''<sub>1</sub> is interpreted as the first principal direction of the prestress on the curved surface. With the assumption that '''T'''<sub>3</sub> is equal to the surface normal vector '''G'''<sub>3</sub> (not normalized), the second direction of the prestress is calculated as '''T'''<sub>2</sub>='''T'''<sub>1</sub> x '''T'''<sub>3</sub>. W.r.t. the parameters for the input file, only the plane area with the vectors '''f'''<sub>1</sub> and '''f'''<sub>2</sub> has to be defined. Referring to the depicted approach the vector '''A''' defines the vector '''f'''<sub>1</sub> and the vector '''B''' defines the vector '''f'''<sub>2</sub>. |
| − | [[File: | + | [[File:MembraneElement PrestressDirectionDefinition.jpg|600px|up|Definition of the prestress directions for the membrane element]] |
=== Prestress state === | === Prestress state === | ||
Revision as of 07:04, 5 December 2016
Contents |
General Description
Element Type
- This membrane element is a plane stress element with 3 degrees of freedom per node
- The membrane element neglects the bending stiffness
- The ratio of the thickness and the lengths in the other two directions is much smaller than one ( t/Lx << 1 and t/Ly << 1), the membrane is reduced to its mid-surface
- The thickness is constant over the element
Degrees of Freedom
The membrane element uses the 3 translatoric degrees of freedom, DISP_X, DISP_Y, DISP_Z.
Input Parameters
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| MAT | EL-MAT int | Number for the used Material
e.g. MAT=EL-MAT 1 |
| THICKNESS | int | Thickness of the membrane |
| A_X, A_Y, A_Z
B_X, B_Y, B_Z |
Definition of the principal directions of the surface to define the prestress directions. (see description below) | |
| SIG11
SIG22 SIG12 |
Prestress state of the membrane. (see description below) | |
| Optional Parameters | ||
| Parameter | Values, Default(*) | Description |
| LAGRANGE | TOTAL, UPDATED | Definition of lagrange type. UPDATED for form finding and TOTAL for statics or dynamics. (e.g. LAGRANGE=UPDATED) |
Example of a Complete Input Block
EL-PROP 1 : MEMBRANE1 MAT= EL-MAT 1 THICKNESS=1.0 PRESTRESS SIG11=1.0 SIG22=1.0 SIG12=0.0 A_X=1.0 A_Y=0.0 A_Z=0.0 B_X=0.0 B_Y=1.0 B_Z=0.0 LAGRANGE=UPDATED
Element Loading
Pressure
Dead Load
Snow Load
Theory
The theory and finite element formulation is described in detail in [1] , [2] and [3].
For the correct use of the membrane element and the interpretation of related results, the following aspects should be considered:
Material parameter
With the parameter MAT the material, that would be used in the calculation, for the membrane element is defined. The following materials are tested for the membrane element:
- linear elastic isotropic
- linear elastic orthotropic (Münsch-Reinhardt)
- multilinear elastic isotropic
- elastoplastic isotropic
- material on the basis of response functions
Thickness parameter
The parameter THICKNESS defines the thickness of the membrane. The thickness is assumed constant over the element.
Prestress directions on the surface
The parameters A_X, A_Y, A_Z and B_X, B_Y, B_Z are used to define the prestress directions on the surface, which is necessary in case of anisotropic prestress conditions. In this approach the principal directions of the prestress are defined in a plane area (see figure below). The definition of the area is given by the two vectors f1 and f2. The normal vector of the area can be calculated with the cross product of the in plane vectors f3=f1 x f2. Afterwards the line of intersection T1 of the area which is given by f1 and f3 and the curved surface can be calculated. In this approach T1 is interpreted as the first principal direction of the prestress on the curved surface. With the assumption that T3 is equal to the surface normal vector G3 (not normalized), the second direction of the prestress is calculated as T2=T1 x T3. W.r.t. the parameters for the input file, only the plane area with the vectors f1 and f2 has to be defined. Referring to the depicted approach the vector A defines the vector f1 and the vector B defines the vector f2.
Prestress state
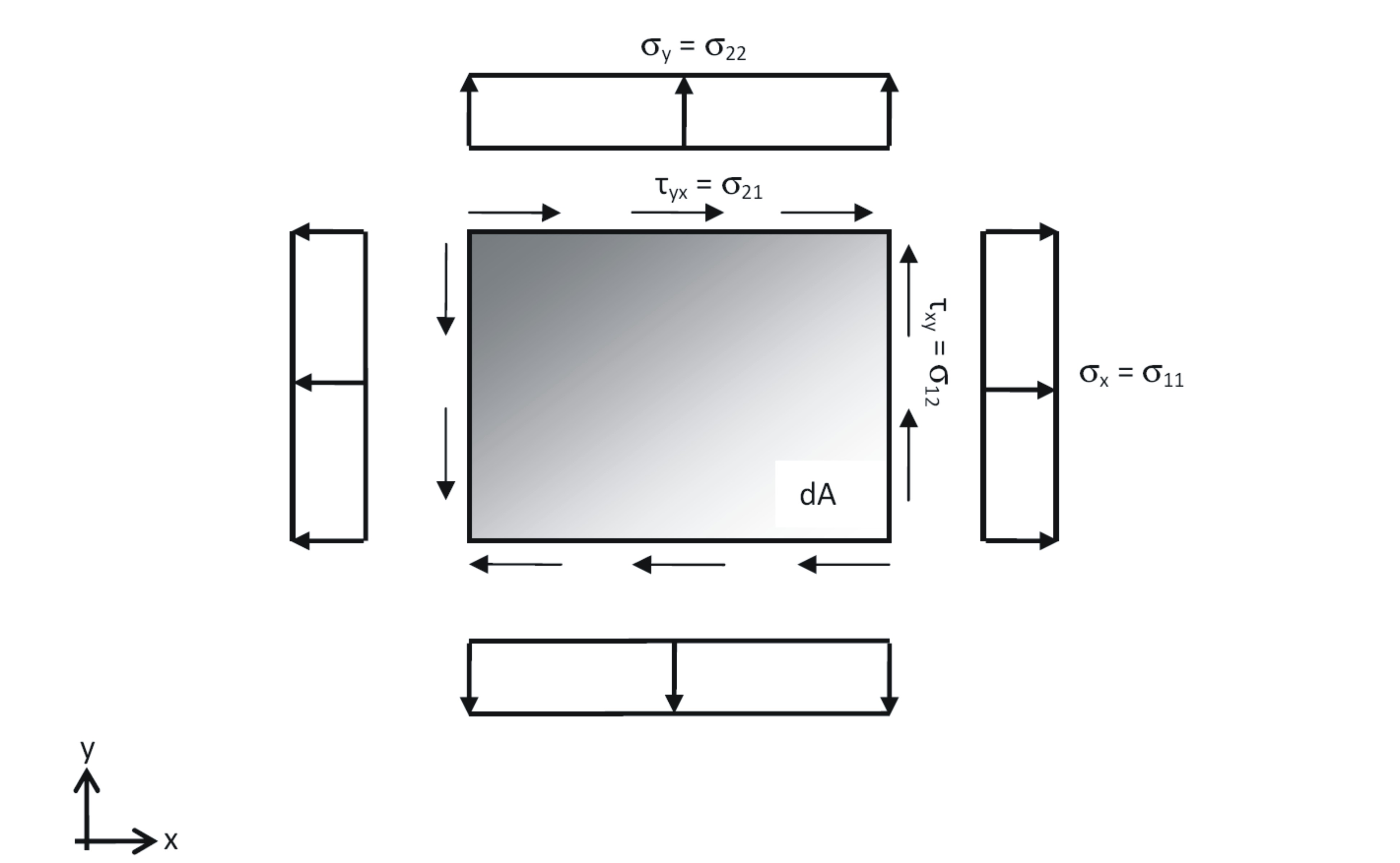
SIG11, SIG22, SIG12 describes the prestress of the membrane element. The element is based on the plane stress assumption. Due to that only normal and shear stresses in the midplane have to be defined. SIG11 is the stress acting in T1, SIG22 acting in T2 and SIG12 is the in-plane shear, whereas SIG12=SIG21 (see figure below).
Lagrange type
With the (optional) LARANGE parameter it is possible to switch between form finding and statical/dynamical analysis. For the value UPDATED the element is for form finding and for the value TOTAL the element is for statical/dynamical analysis. It is important that the LANGRANGE parameter match to the type of analysis.
References
- ↑ Dieringer, F.: Implementierung eines geometrisch nichtlinearen Membranelements in einer objektorientierten Programmierumgebung, Masterthesis, Chair of structural analysis, Technische Universität München, 2009
- ↑ Linhard, J.: Numerisch-mechanische Betrachtung des Entwurfsprozesses von Membrantragwerken, PhD-Thesis, Chair of structural analysis, Technische Universität München, 2009
- ↑ Dieringer, F.: Numerical Methods for the Design and Analysis of Tensile Structures, Dissertation Lehrstuhl für Statik, 2014
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |