Users:General FEM Analysis/Elements Reference/Quad1

From Carat++ Public Wiki
< Users:General FEM Analysis | Elements Reference(Difference between revisions)
Jump to: navigation, search
(→Degrees of Freedom)
(→Example of a Complete Input Block)
 
(6 intermediate revisions by one user not shown)
Line 4: Line 4:
 
== General Description ==
 
== General Description ==
 
   
 
   
−
 
+
[[File:Quad.PNG|300px|center|4-noded quad element]]
  
 
=== Element Type ===
 
=== Element Type ===
  
−
This class provides a purely displacement formulated four-noded plane stress/plane strain element. '''It is only intended for comparisons and  introductory purpose'''. The element is only able to perform geometrically linear static computations and cannot carry element loads.
+
This class provides a purely displacement formulated four-noded plane stress/plane strain element. '''It is intended for comparisons and  introductory purpose only'''. The element is only able to perform geometrically linear static computations and cannot carry element loads.
  
 
=== Degrees of Freedom ===
 
=== Degrees of Freedom ===
Line 29: Line 29:
 
|Linking to a material input block
 
|Linking to a material input block
 
|-
 
|-
−
!INT_TYPE_HEXA
+
!THICKNESS
−
|FULL, REDUCED
+
|''real''
−
|Control of integration type <br>
+
|Parameter for constant element thickness
−
20-noded elements are able to perform a uniform reduced integration (2x2x2 instead of 3x3x3) without hourglassing stabilisation
+
 
|-
 
|-
−
|colspan="3" style="background:#efefef;"| Optional Parameters
+
!INT_TYPE_QUAD
 +
|FULL
 +
|Only full integration is available
 
|-
 
|-
−
!Parameter
+
!MODE
−
!Values, Default(*)
+
|PSTRESS, PSRTAIN
−
!Description
+
|Switch to choose plane stress or plane strain computation
−
|-
+
−
!EAS
+
−
|''int''
+
−
|Flag Enhances Assumed Strains (EAS) method <br>
+
−
Possible values are:
+
−
* 0*  = EAS off
+
−
* 9  = full and locking free linear strains can be described (recommended for one axial bending)
+
−
* 15 = ellimination of parasitic bi-linear strains
+
−
* 24 = full and locking free bi-linear strains can be described (recommended for two axial bending)
+
−
* 30 = full tri-linear strains can be described
+
 
|-
 
|-
 
|}
 
|}
Line 55: Line 46:
 
=== Example of a Complete Input Block ===
 
=== Example of a Complete Input Block ===
 
<pre>
 
<pre>
−
EL-PROP 1: SOLIDHEXA1
+
EL-PROP 1: QUAD1
 
MAT          = EL-MAT 1
 
MAT          = EL-MAT 1
−
INT_TYPE_HEXA = FULL
+
THICKNESS    = 0.1
−
EAS          = 0
+
INT_TYPE_QUAD = FULL
 +
EAS          = PSTRESS    ! choose: PSTRESS, PSTRAIN
 
</pre>
 
</pre>
−
Inside the property block there is no distinction between linear and quadratic formulated elements. It is possible to define 8-noded, 20-noded and 27-noded elements using one and the same element property (assuming that no EAS is used):
 
 
<pre>
 
<pre>
−
  !  ElementID  Part-ID      EL-PROP             Node-IDs
+
  !  ElementID  Part-ID      EL-PROP       Node-IDs
−
NEL  1          1            1            1  2  3  4 5  6  7  8                                                                  ! 8-noded element
+
NEL  1          1            1            1  2  3  4  
−
NEL  2          1            1            20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 36 38 39 40                          !20-noded element
+
−
NEL  3          1            1            50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 66 68 69 70 71 72 73 74 75 76 77    !27-noded element
+
 
</pre>
 
</pre>
−
 
−
== Element Loading ==
 
−
 
−
Hexahedral elements are able to carry two types of element loads:
 
−
* dead load
 
−
* temperature load
 
−
 
−
=== Dead Load ===
 
−
Dead weight of an element is computed by multiplying material's denisity (ρ) with gravity's acceleration, which has to be defined inside the load block concearning its direction and size. <br>
 
−
An example for a load definition of a concrete structure (assuming linear elastic isotropic material behaviour) with gravity acting in positive z-direction would look like
 
−
 
−
<pre>
 
−
EL-MAT 1 : LIN_ELAST_ISOTROPIC
 
−
EMOD=3.5e10  ALPHAT=1e-5  DENS=2.5e3  NUE=0.2
 
−
</pre>
 
−
<pre>
 
−
LD-ELEM 1 PART=1
 
−
TYPE=DEAD      D1=0.0  D2=0.0  D3=1.0  VAL=9.81
 
−
</pre>
 
−
 
−
whereat the finite elemet model is based on SI units (m, N, kg).
 
−
 
−
=== Temperature Load ===
 
−
This paragraph only focuses at element specific topics concearing temperature load. For more detailed descriptions please look at the load documentation  <br> <br>
 
−
For the computation of temperature loads solid elements do not concider any layer of laminate structure within the element. So only the temperature defined for layer number one is considered at each node. <br>
 
−
The combination of temperature loading and EAS improvement is possible.
 
−
 
−
<pre>
 
−
LD-ELEM 1 
 
−
sTYPE = TEMPERATURE
 
−
ND-SET = 1  LAYER = 1  VAL = +10
 
−
ND-SET = 2  LAYER = 1  VAL = -10
 
−
</pre>
 
−
 
−
== The EAS Method ==
 
−
The idea of enhanced assumed strains is to enlarge the element srain field by a set of additional strains in order to enable the element to express certain states of displacement without locking due to parasitic strains.
 
−
<ref>
 
−
J.C. Simo, M.S. Rifai: „A class of mixed assumed strain methods and the method
 
−
of incompatible modes“, in „International Journal for Numerical Methods in Engineeering“, Vol. 29, 1990, pages 1595-1638
 
−
</ref>
 
−
<ref name="AnRa93"> U. Andelfinger, E. Ramm: „EAS-Elements for two-dimensional, three-dimensional,
 
−
plate and shell structures and their equivalence to HR-Elements“, in „International
 
−
Journal for Numerical Methods in Engineeering“, Vol. 36, 1993, pages 1311-1337 </ref>.
 
−
 
−
To this purpose the strain-displacement relation is enlarged by additional terms which leads to a modified element stiffness matrix:
 
−
[[File:Eas_formulas.JPG|400px|border|center|stiffness matrix concerning EAS improvement]]
 
−
 
−
The following example will show the  benefit of EAS improved elements toward purely displacment formulated eight-noded hexahedrals. The investigated system is a tip loaded cantilever wherby the cross section is modeled by one element.
 
−
 
−
{|border="1"
 
−
|[[File:Cantilever_locking.JPG |400px| HEXA8]]
 
−
|[[File:Cantilever_lockingfree.JPG |400px| HEXA8EAS9]]
 
−
|-
 
−
| Element HEXA8
 
−
| Element HEXA8EAS9
 
−
|}
 
−
 
−
The pure displacement based elements show the well known in-plane shear locking which increases along the cantilever with increasing bending moment. As artificial strain/shear produces artificial stiffness, the tip displacement is extremly under estimated.
 
−
 
−
In contrast the EAS improved elements are able to eliminate artificial strains arrising from locking, and so tip displacement is described correctly.
 
  
 
== References ==
 
== References ==
 
<references/>
 
<references/>

Latest revision as of 07:24, 7 September 2010


Contents

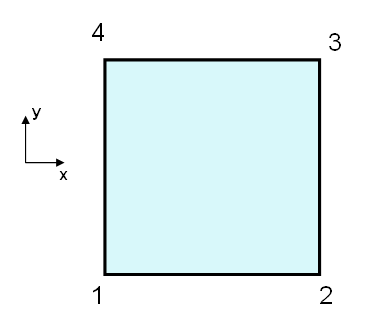
General Description

4-noded quad element

Element Type

This class provides a purely displacement formulated four-noded plane stress/plane strain element. It is intended for comparisons and introductory purpose only. The element is only able to perform geometrically linear static computations and cannot carry element loads.

Degrees of Freedom

All nodes of the plane stress/stain element have to be defined in the plane z=0 and all movements take place in this plane. So nodal displacements can be described by the two remaining translatoric degrees of freedom, Disp_X and Disp_Y.

Input Parameters

Parameter Description

Compulsory Parameters
Parameter Values, Default(*) Description
MAT EL-MAT int Linking to a material input block
THICKNESS real Parameter for constant element thickness
INT_TYPE_QUAD FULL Only full integration is available
MODE PSTRESS, PSRTAIN Switch to choose plane stress or plane strain computation


Example of a Complete Input Block 

EL-PROP 1: QUAD1
MAT           = EL-MAT 1
THICKNESS     = 0.1
INT_TYPE_QUAD = FULL
EAS           = PSTRESS    ! choose: PSTRESS, PSTRAIN

 !  ElementID  Part-ID       EL-PROP        Node-IDs
NEL  1           1             1            1  2  3  4

References





Whos here now:   Members 0   Guests 0   Bots & Crawlers 1
 
Retrieved from "http://carat.st.bv.tum.de/caratuserswiki/index.php/Users:General_FEM_Analysis/Elements_Reference/Quad1"
Personal tools
Content for Users
Content for Developers