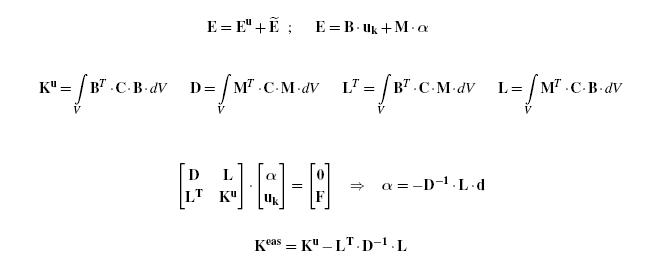Users:General FEM Analysis/Elements Reference/Quad1
(→Input Parameters) |
(→Element Loading) |
||
| Line 55: | Line 55: | ||
! ElementID Part-ID EL-PROP Node-IDs | ! ElementID Part-ID EL-PROP Node-IDs | ||
NEL 1 1 1 1 2 3 4 | NEL 1 1 1 1 2 3 4 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</pre> | </pre> | ||
Revision as of 07:23, 7 September 2010
Contents |
General Description
Element Type
This class provides a purely displacement formulated four-noded plane stress/plane strain element. It is intended for comparisons and introductory purpose only. The element is only able to perform geometrically linear static computations and cannot carry element loads.
Degrees of Freedom
All nodes of the plane stress/stain element have to be defined in the plane z=0 and all movements take place in this plane. So nodal displacements can be described by the two remaining translatoric degrees of freedom, Disp_X and Disp_Y.
Input Parameters
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| MAT | EL-MAT int | Linking to a material input block |
| THICKNESS | real | Parameter for constant element thickness |
| INT_TYPE_QUAD | FULL | Only full integration is available |
| MODE | PSTRESS, PSRTAIN | Switch to choose plane stress or plane strain computation |
Example of a Complete Input Block
EL-PROP 1: QUAD1 MAT = EL-MAT 1 THICKNESS = 0.1 INT_TYPE_QUAD = FULL EAS = PSTRESS ! choose: PSTRESS, PSTRAIN
! ElementID Part-ID EL-PROP Node-IDs NEL 1 1 1 1 2 3 4
The EAS Method
The idea of enhanced assumed strains is to enlarge the element srain field by a set of additional strains in order to enable the element to express certain states of displacement without locking due to parasitic strains. [1] [2].
To this purpose the strain-displacement relation is enlarged by additional terms which leads to a modified element stiffness matrix:
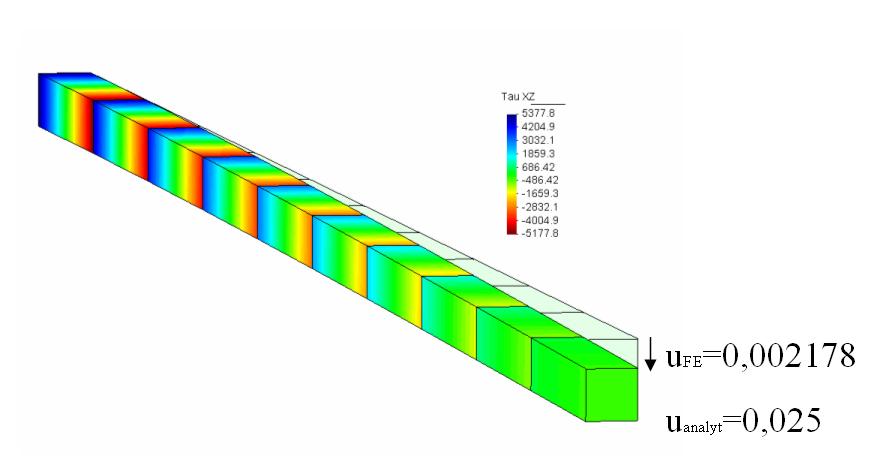
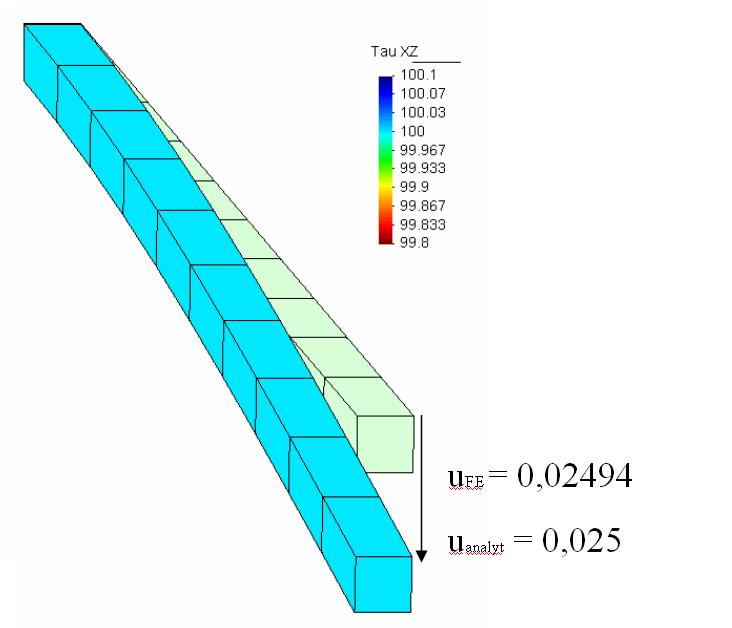
The following example will show the benefit of EAS improved elements toward purely displacment formulated eight-noded hexahedrals. The investigated system is a tip loaded cantilever wherby the cross section is modeled by one element.
|
|
| Element HEXA8 | Element HEXA8EAS9 |
The pure displacement based elements show the well known in-plane shear locking which increases along the cantilever with increasing bending moment. As artificial strain/shear produces artificial stiffness, the tip displacement is extremly under estimated.
In contrast the EAS improved elements are able to eliminate artificial strains arrising from locking, and so tip displacement is described correctly.
References
- ↑ J.C. Simo, M.S. Rifai: „A class of mixed assumed strain methods and the method of incompatible modes“, in „International Journal for Numerical Methods in Engineeering“, Vol. 29, 1990, pages 1595-1638
- ↑ U. Andelfinger, E. Ramm: „EAS-Elements for two-dimensional, three-dimensional, plate and shell structures and their equivalence to HR-Elements“, in „International Journal for Numerical Methods in Engineeering“, Vol. 36, 1993, pages 1311-1337
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |