Users:Structural Optimization/Response Functions/Stress
Contents |
General Description
Short Info
The Kreisselmeier-Steinhauser function for the stresses is a global measure of stress in a structure. Stress results are generally very local results but using this response function an overall stress indicator is obtained. It can be used as an objective to reduce the overall stress in the structure or as a constraint to limit the stress in the structure to a maximum allowed value.
The Kreisselmeier-Steinhauser function for the stresses is formulated by
- KS = 1/ρ log (∑i exp (ρ σi/ σmax ))
with ∑i a summation over all Gausspoints in the domain and σi the stress in the i-th Gausspoint from a linear or nonlinear analysis. σmax is the maximum allowed stress. ρ is a parameter that determines the importance of the largest stresses amongst all σi. The response function requires the ID of a linear static analysis or a nonlinear static analysis specified for parameter 'ANALYSIS'.
This function was originally designed as a continuous alternative for max(σi). The larger ρ, the more KS approaches max(σi). For a large ρ, the value of KS depends merely on the maximal stress value so the effect of the function is limited to the neighbourhood of this maximal stress. If ρ is small, KS is always larger than max(σi). When reducing ρ the effect of the function becomes more global since more stresses contribute significantly to its value. It is required to specify a value for ρ with the input parameter RHO. A reasonable range of ρ is between 1 and 100.
The value of the exponential function becomes infinite very fast, even for reasonable values of the argument. Therefore, the value of σmax should not be too small. The best results are obtained if the stresses σi are similar to σmax. If all the stresses in the structure are much smaller than the allowed stress, there will be no reasonable value of ρ that is large enough to make KS similar to max(σi). As a consequence, KS will be similar for all proposed structures and thus become useless. If the value of the maximum allowed stress is specified by the paramater STRESS_LIMIT, the formula stated above is used. If a positive value is specified for STRESS_LIMIT, the negative stresses have a very limited contribution to the value of KS. If the value for STRESS_LIMIT is negative, the largest negative stresses determine KS completely. In constrast, if ABS_STRESS_LIMIT is used, the formulation of KS is changed to:
- KS = 1/ρ log (∑i exp (ρ abs(σi) / σmax ))
such that both the negative and the positive stresses influence the value of the response function.
So to summarize: if this response function is used as an objective function, the value of σmax should be chosen such that it is close to the real stresses in the structure. Additionally, the value for ρ should be rather low to obtain a measure of stress with a global effect. If this response function is used as a constraint function, the value of σmax should be chosen as the real maximum allowed value. If the material has the same stress limit in tension and compression, ABS_STRESS_LIMIT can be used. However, if the limit in tension and compression is different, two constraints should be added with the respective positive and negative STRESS_LIMIT.
Using this response function as a constraint is conservative since KS will always be at the safe side. To limit this overdimensioning, scaling methods (KS_SCALING) can be used. One option (UPDATE_RHO) is to increase ρ in every fifth iteration. At the end, the KS function will be very close to the maximum stress. However, if ρ is too high, this introduces similar numerical problems as using the discontinuous constraint max(σi) and the global effect of the function is lost. Another option is to use a scaling factor (SCALING_FACTOR). This method replaces the KS value with the value max(σi) while the gradients remain the same. In this way, the stress in the resulting structure is very close to the maximum allowed value.
Input Parameters
| Block headline | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| OPT-RESPONSE_FCT | int : STRESS_KS | Function ID and type mechanical problem. |
| Common compulsory parameters | ||
| ETA | real | Finite difference disturbance for sensitivity analysis |
| GRAD | DIRECT, ADJOINT | Method of gradient computation |
| SA | GLOBAL_FD, SEMI_ANALYTIC, EXACT_SEMI_ANALYTIC, ANALYTIC | Method of derivative computations inside sensitivity analysis |
| FDA | FOREWARD, CENTRAL, BACKWARD | Method of finite difference approximation (if neccessary for the chosen sensitivity analysis method) |
| DESVAR | OPT-VAR vector of integers | Design variables that are considered in the sensitivity analysis of this response function |
| Common optional parameters | ||
| WEIGHT | real, 1.0* | The weighting factor for this response function in multi-objective optimization |
| ANALYSIS | PC-ANALYSIS int | ID of the underlying analysis |
| Specific parameters | ||
| ELEMENTS | El-SET or PART | Determines the elements of which the stress is taken into account |
| STRESS_TYPE | VMISES_TOP, VMISES_BOTTOM, VMISES, PRINCIPLE_1_TOP, PRINCIPLE_1_BOTTOM, PRINCIPLE_1, PRINCIPLE_2_TOP, PRINCIPLE_2_BOTTOM, PRINCIPLE_2 | Determines which stress type is taken into account |
| RHO | real | Parameter that determines how local the effect of this response function is |
| STRESS_LIMIT | integer | Maximum value for the real value of the stress (cannot be combined with ABS_STRESS_LIMIT) |
| ABS_STRESS_LIMIT | integer | Maximum value for the absolute value of the stress (cannot be combined with STRESS_LIMIT) |
| KS_SCALING | NO_SCALING, SCALING_FACTOR or UPDATE_RHO | Determines if a scaling method is used |
| RHO_UPDATE_VAL | real | Multiplication factor for RHO, applied every 5 iterations |
| Common Compulsory Parameters for Constraints | ||
| Parameter | Values, Default(*) | Description |
| REL_LIMIT | real | Relative limit for constraint, depending on the actual value. |
| ABS_LIMIT | real | Absolute limit for constraint. Only one limit can be defined for a constraint. |
| CONSTRAINT_TYPE | INEQUALITY_LT, INEQUALITY_GT, EQUALITY | Type of constraint |
| Common Optional Parameters for Constraints | ||
| REL_TOLERANCE | real, 0* | Upper relative limit until which an inactive constraint is concidered as an active one |
| LAMBDA_ABS_MAX | real, 1/cepsilon* | Upper limit for lagrangian multiplier |
Example of a Complete Input Block
OPT-RESPONSE_FCT 1 : STRESS_KS ! -- basic stuff WEIGHT=1.0 ANALYSIS=PC-ANALYSIS 1 ETA=1e-06 GRAD=ADJOINT SA=SEMI_ANALYTIC FDA=FOREWARD DESVAR=OPT-VAR 1,2,3,4,5,6 ! -- specific ELEMENTS = EL-SET 1 STRESS_TYPE = PRINCIPLE_1_TOP RHO = 10.0 ABS_STRESS_LIMIT = 200.0E06 KS_SCALING = NO_SCALING ! -- constraint parameters ABS_LIMIT = 1-e3 REL_TOLERANCE = 0.1 CONSTRAINT_TYPE = INEQUALITY_LT LAMBDA_ABS_MAX = 20
Examples
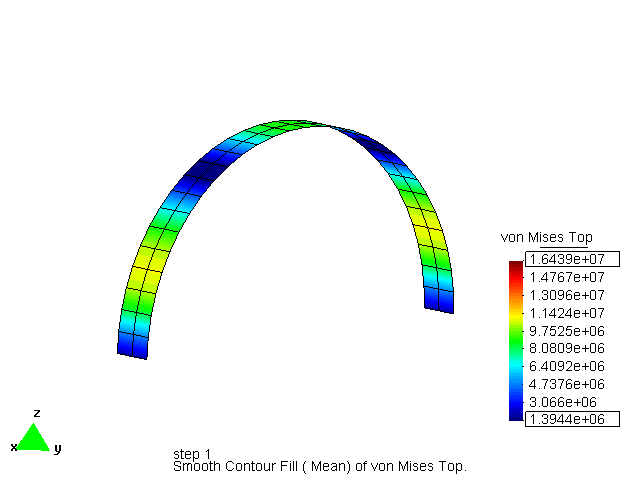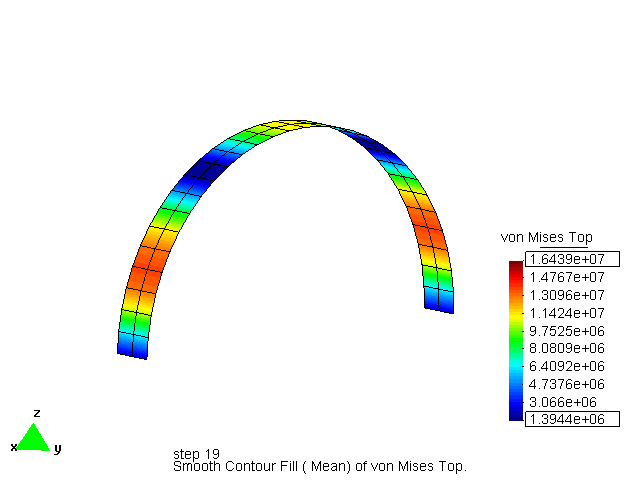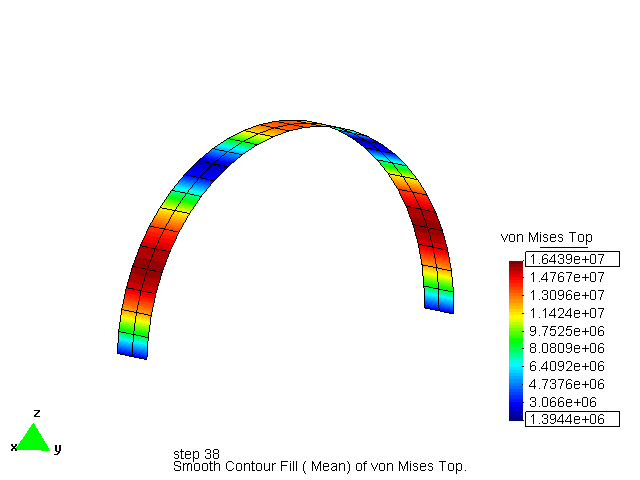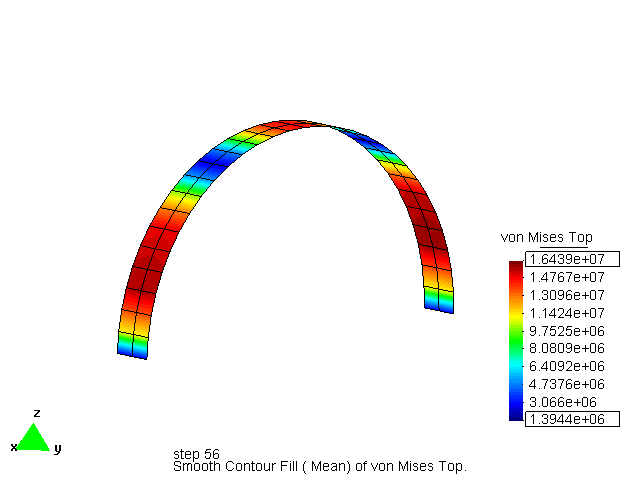
Catenary arch with stress as objective
This example shows the evolution of a circular arch loaded by self weight to a catenary arch during the minimization of the Kreisselmeier-Steinhauser function for the stress. It is clear that the effect of KS is global, even by using local stress results.
Catenary arch with stress as constraint
Consider now the same circular arch but with variable thickness. By changing the thickness in each node, the mass is minimized. It is assumed that the Von Mises top stress is limited to 15 MPa. For that reason, the KS function is used as a constraint. Rho is set to 100. Due to the formulation of the KS function, the maximal value of the constraint is expected to be 1. However, based on a preliminary run, the maximal value of the constraint is set to 1.1 to work around the margin that the KS function implies with low values for rho. Starting from a thickness of 0.08 m, the resulting thicknesses are between the minimal thickness of 0.03 m and 0.041 m. The maximal Von Mises top stress is 16 MPa, which is close to the imposed limit. The volume of the structure is reduced nearly 60%, from 9910 to 4056 m3.
The left figures show the evolution of the thickness (left) and the stress (right). During the first iterations, the thickness is reduced equally everywhere since the constraint is not yet active.
Shell cantilever
This example shows the optimal shape of a cantilever beam subjected to an end load. The structure is modelled by shell elements. During the optimization, the Kreisselmeier-Steinhauser function is minimized while the structural weight was not allowed to increase more than 5%. To avoid singularity at the free end, a bound constraints the movement of the end nodes. The optimization problem is solved by the Augmented Lagrangian Multiplier method for ρ=1 (left) and ρ=10 (right). Comparing the evolution of the shape, it is clear that the design updates are more localized in the neighbourhood of the maximal stress when using a higher value of ρ.
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |