Users:Structural Optimization/Response Functions/Displacement
Contents |
General Description
Short Info
This response function refers directly to a nodal displacement, so the function value is equal to the traced degree of freedom. The underlying analysis has to be a static one, response functions for linear and non-linear statics are available.
Input Parameters
| Block headline | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| OPT-RESPONSE_FCT | int : DISPLACEMENT_LIN or DISPLACEMENT_NONLIN | Function ID and type mechanical problem (geometrically linear or geometrically nonlinear) |
| Common compulsory parameters | ||
| ETA | real | Finite difference disturbance for sensitivity analysis |
| GRAD | DIRECT, ADJOINT | Method of gradient computation |
| SA | GLOBAL_FD, SEMI_ANALYTIC, EXACT_SEMI_ANALYTIC, ANALYTIC | Method of derivative computations inside sensitivity analysis |
| FDA | FOREWARD, CENTRAL, BACKWARD | Method of finite difference approximation (if neccessary for the chosen sensitivity analysis method) |
| DESVAR | OPT-VAR vector of integers | Design variables that are considered in the sensitivity analysis of this response function |
| Common optional parameters | ||
| WEIGHT | real, 1.0* | The weighting factor for this response function in multi-objective optimization |
| ANALYSIS | PC-ANALYSIS int | ID of the underlying analysis |
| Specific parameters | ||
| NODE | int | ID of traced node |
| DOF | DISP_X, DISP_Y, DISP_Z | Traced nodal DOF |
| GOAL | MIN, MAX | Choose if the traced DOF value has to be maximized or minimized |
| LOAD_CONSTANT | 0, 1 | UNUSED! Select if the load factor is constant through optimization (1) or not (0). Only used in DISPLACEMENT_NONLIN. |
| Common Compulsory Parameters for Constraints | ||
| Parameter | Values, Default(*) | Description |
| REL_LIMIT | real | Relative limit for constraint, depending on the actual value. |
| ABS_LIMIT | real | Absolute limit for constraint. Only one limit can be defined for a constraint. |
| CONSTRAINT_TYPE | INEQUALITY_LT, INEQUALITY_GT, EQUALITY | Type of constraint |
| Common Optional Parameters for Constraints | ||
| REL_TOLERANCE | real, 0* | Upper relative limit until which an inactive constraint is concidered as an active one |
| LAMBDA_ABS_MAX | real, 1/cepsilon* | Upper limit for lagrangian multiplier |
Example of a Complete Input Block
An example of a linear displacement inequality constraint with an absolute limit.
OPT-RESPONSE_FCT 1 : DISPLACEMENT_LIN ! -- basic stuff WEIGHT=1.0 ANALYSIS=PC-ANALYSIS 1 ETA=1e-06 GRAD=ADJOINT SA=SEMI_ANALYTIC FDA=FOREWARD DESVAR=OPT-VAR 1,2,3,4,5,6 ! -- response function dependant parameters NODE = 26461 DOF = DISP_Z GOAL = MIN ! -- constraint parameters ABS_LIMIT = 1-e3 REL_TOLERANCE = 0.1 CONSTRAINT_TYPE = INEQUALITY_LT LAMBDA_ABS_MAX = 20
A complete test example
Model description
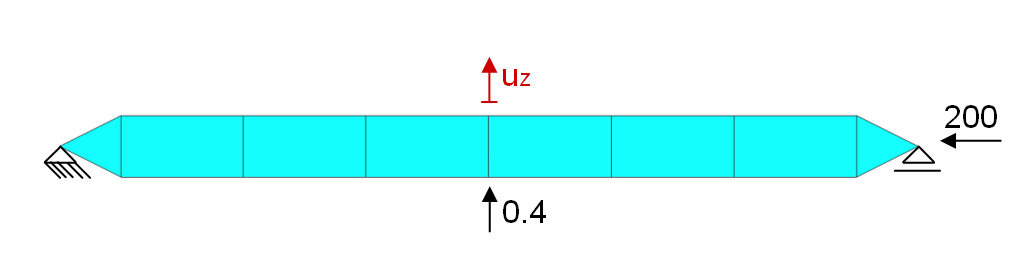
This is a simple example of a displacemenet maximization. The system consists of a statically determined supported beam mainly laoded by pressure with an additional veritcal imperfection. The optimization goal is to maximize the vertical movement of the beam's center of gravity.
Input File
The corresponding input file can be downloaded here.
Documented Results
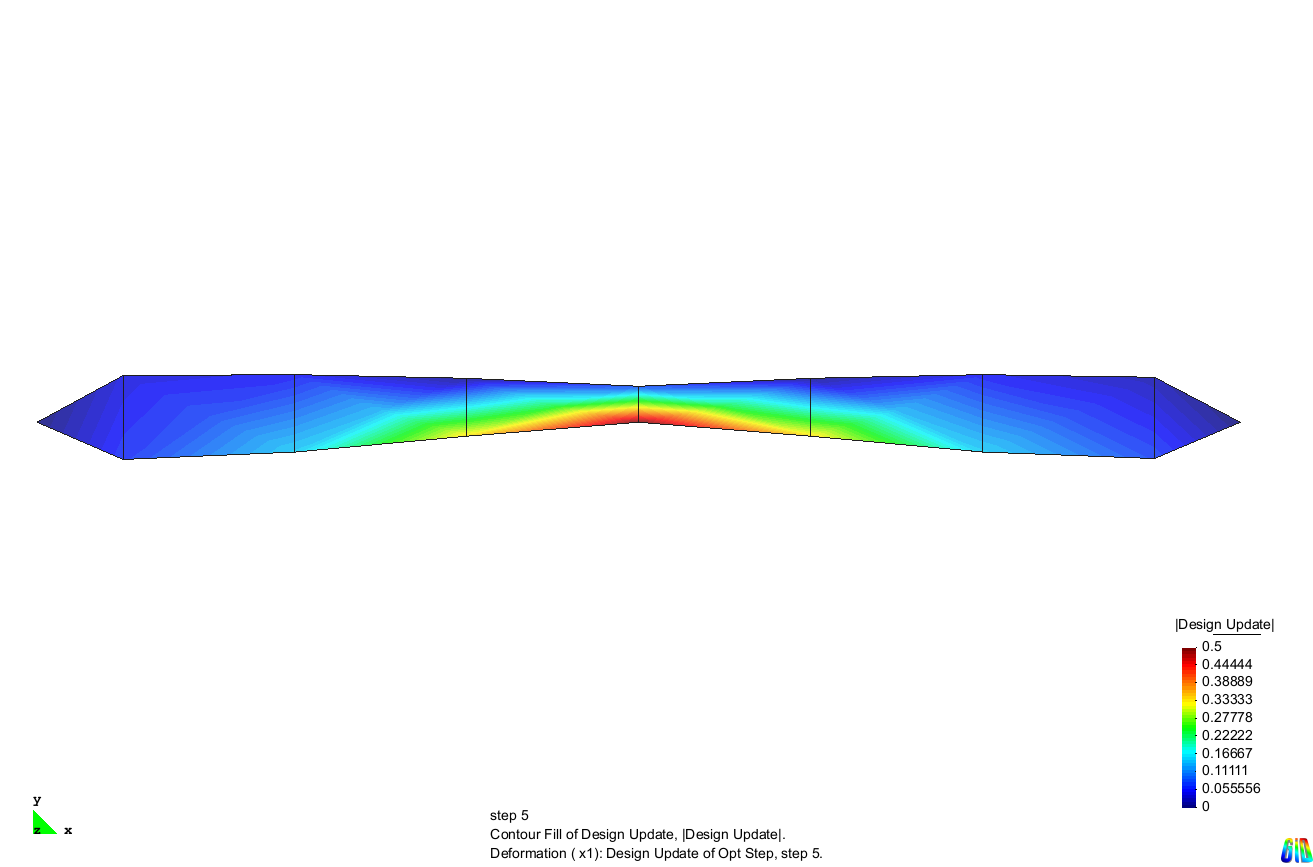
The optimization result is the structure shown below. A hinge-like structure was generated by shrinking the cross section towards the middle. As a result of this optimization, the vertical displacement of the center point increased by a factor of 176.
References
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |