Users:Structural Optimization/General Formulation

General Optimization Problem

Structural optimization problems are formulated to improve structural properties under consideration of specified constraints. The desired structural properties are formulated in the so called objective function denoted by f. By definition these function will be minimized. To achieve improved structural properties it is necessary to change structural parameters. The parameters to be changed are called design variables s. In many applications upper and/or lower bounds are defined on these design variables. These variable bounds are denoted by s_lower and s_upper respectively. In general, the optimum solution is restricted by constraints. These constraints are separated in equality constraints denoted by h and inequality constraints denoted by g. The full optimization problem states as follows:

min. f(s)

s.t. g(s) ≤ 0

h(s) = 0

s_lower ≤ s ≤ s_upper.

Design Variables

The choice of design variables defines basic properties of the optimization problem. Based on the design variables structural optimization problems are separated in material, sizing, shape and topology optimization. The numerical effort of the sensitivity analysis as well as the overall robustness of the optimization problem is strongly related to the choice of design variables.

Design Variables of Structural Optimization Problems

Material Optimization

Material optimization problems utilize material parameters as design variables whereas topology and geometry of the structural model remain constant. Examples for material variables are distribution of concrete reinforcement, direction of fiber angles or layer sequence in composite materials.

Sizing Optimization

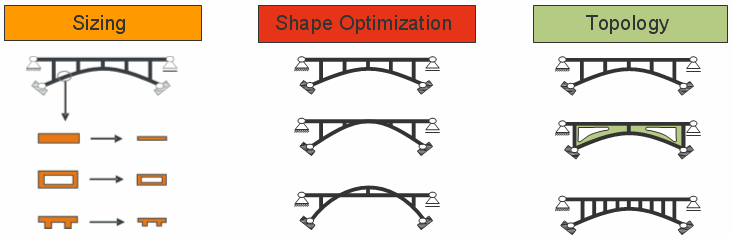
Sizing optimization is used to investigate the optimal dimension of cross section parameters, which in detail are related to the applied structural model. The cross section of truss structures is defined by the cross section area. Beam structures also carry bending loads which requires definition of more complex cross sections, e.g. by width and height or the second moment of inertia. Wall and shell structures usually define their cross section by the thickness. Due to constant model geometry and model topology differentiation of the response function with respect to sizing parameters results in facile and efficient formulations. A simple sizing optimization problem is sketched in the figure above. It shows three different cross section types for specific parts of a fixed truss structure. During the sizing optimization process the optimal dimension of each cross section is evaluated. The possible result is a structure with minimal weight that fulfills constraints with respect to maximum displacements and stresses.

Shape Optimization

Shape optimization problems employ the governing geometry variables of a shape parametrization as optimization variables, e.g. node coordinates of finite elements, control point coordinates of CAD models or morphing boxes or amplitudes of shape basis vectors. The topology of the structure (connectivity of elements) remains constant which prevents the generation of holes. The figure above motivates a simple shape optimization problem of a truss beam structure. It can be easily observed that the topology (connectivity) of all three design is equal although the geometry and therefore the load carrying behavior changes completely.

Formulation of shape derivatives results in complex and therefore time consuming algorithms compared to material or sizing variables whereby algorithmic complexity is strongly related to the applied finite elements. In general response functions of shape optimization problems are highly non-convex especially for thin and lightweight structures caused by large differences in efficiency of load carrying mechanisms.

Actually the most design variables in Carat++ are related to shape parameters.

Topology Optimization

The most flexible optimization problem is obtained by application of topology optimization methods. In such problems neither the geometry nor the topology of the structure are predefined. Basic parameters of topology optimization problems are design space and the boundary conditions of the mechanical model. The optimization method computes the most efficient material distribution in the design space. This idea is illustrated by the truss structures in figure above. All three designs are suitable to transfer the load to the supports whereas the material distribution in the design space is totally different.

The most famous topology optimization method is SIMP (Solid Isotropic Material with Penalization) which establishes a heuristic relation between material properties like Young's modulus and material density. In this approach the density of each single element is specified as independent optimization variable which necessitates application of regularization methods, c.f. page Users:Structural Optimization/Optimization Algorithms/Filtering. Application of SIMP to minimum compliance problems yields to the optimal Michell type structures.

The predominant number of applications of topology optimization are related to continuum models discretized by wall or solid elements. An application to shell structures is basically possible but yields to results which need serious interpretation.

Response Functions

Functions applicable as objectives or constraints are commonly denoted as response functions. More information about the available response functions is presented on page Users:Structural Optimization/Response Functions.