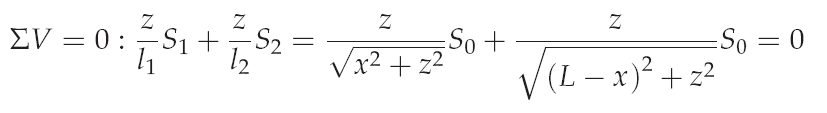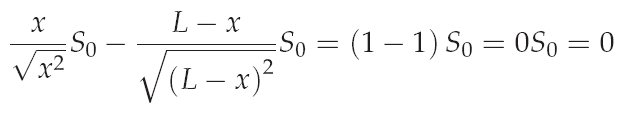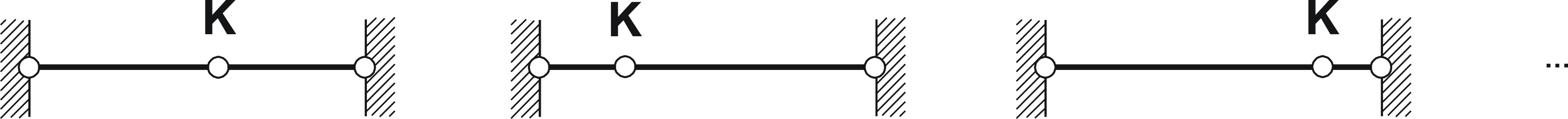Users:Form Finding/Statical Problem of Form Finding
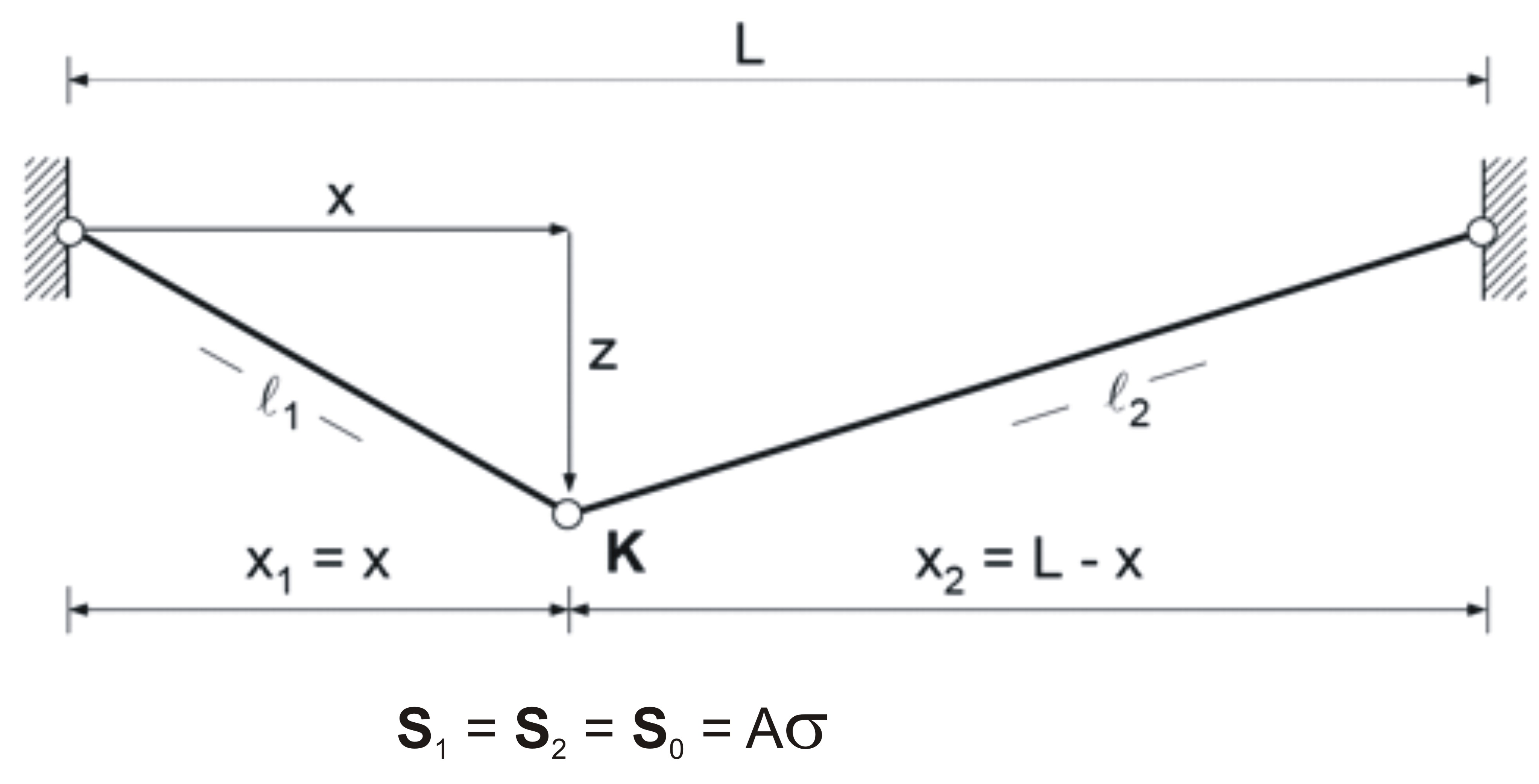
For an introduction in the statical problem of form finding, in the following, a simple 2 bar truss example will be shown. The example tries to find the shape of equilibrium of a cable structure. The cable span between two fixed points at left and right side. The discretizaition (in the context of Finite Elements) is realized with 2 cable elements. The goal is know to find the final coordinate of the middpoint K in order to get a shape of equilibrium. The only given paratmeter is the stress state of the cables, which are equal in both elements (see figure below}).
A is the cross section and σ is the prestress in the cable. The position of the node K is given by the unknown coordinates x and z.
In order to compute the unkown values x and z for the position of node K, basics statical equilibrium is used.
The horizontal equilibrium at node K gives:
And the vertical equilibrium at node K gives:
As easily can be seen, equation for the vertical equilibrium is satisfied for z=0. Which is the mathematical proof for the natural choice of the coordinate z by thinking of the real behaivior. With the knowledge of the coordinate z, equation for the horizontal equilibrium can be solved. Insert z=0 into equation for the horizontal equilibrium leads too:
From this equation can be seen, that the coordinate of x is arbitrary as long as z=0. In other words each coordinate for x is possible as long as K lies on a straight line between the boundaries (see figure below).
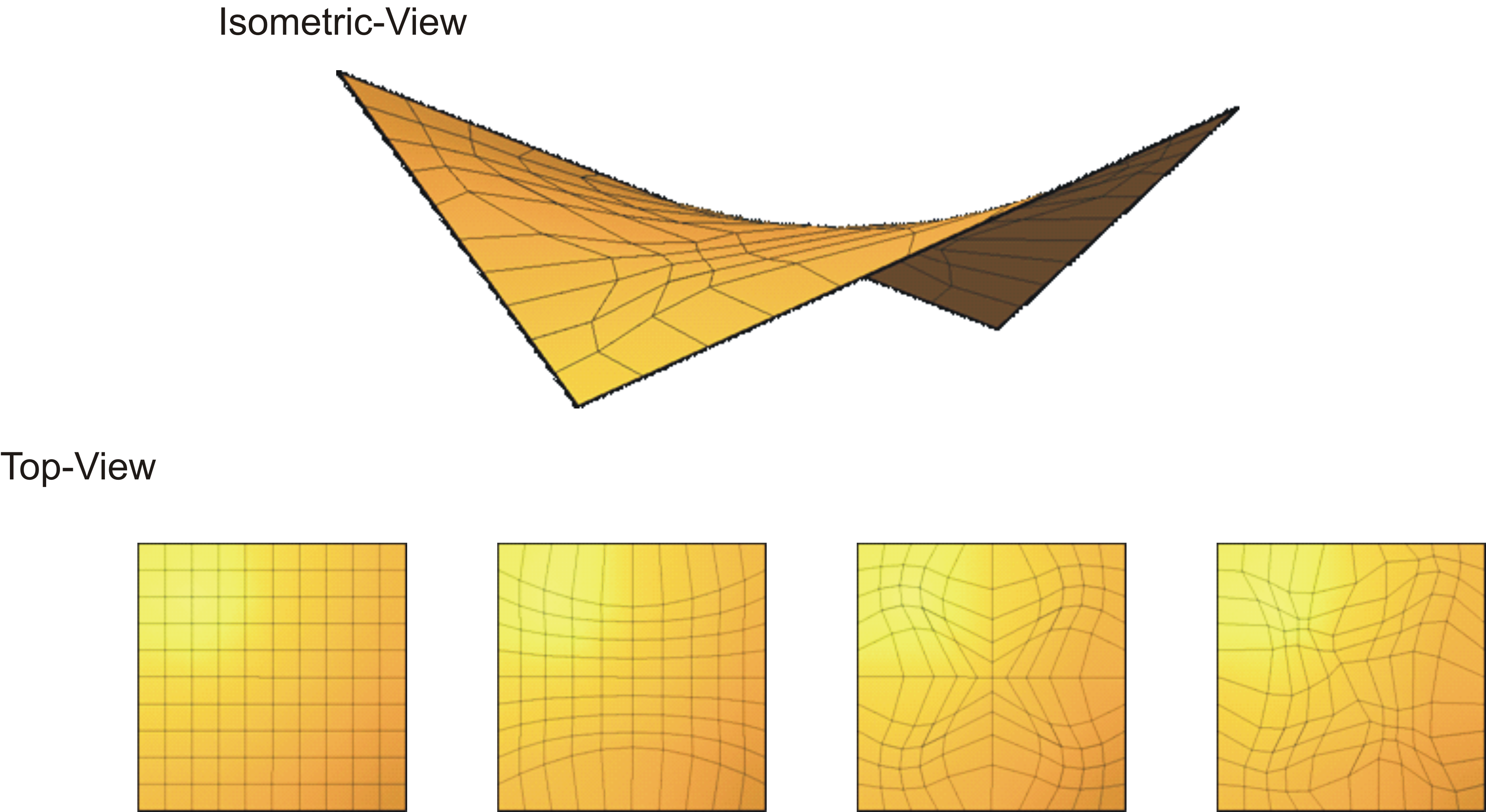
The condition that the coordinate x of node K is arbitrary leads to an infinite number of solutions for the problem. This means from a numerical point of view, that the equations which describes the problem is singular and there is no way to get a certain solution for the above problem. The same problem occurs if we try to solve the form finding problem for surfaces. In following figure it can be seen, that there are an infinite number of possible discretizations of the same surface.
This fact can be understood in that way, that the nodes of the Finite Element mesh are "swimming" on the surface while desrcibing the same geometry. For the numerical
treatment, the same singularty in the governing equations occurs like in the simple 2-bar-truss example.
To get a unique solution for the form finding problem of different structures several methods are deveoloped in the past. In the next section a short explanation
w.r.t. the 2-bar-truss are given.
For a more detailed discussion, refer e.g. to [1] and [2].
References
- ↑ Linhard, J.: Numerisch-mechanische Betrachtung des Entwurfsprozesses von Membrantragwerken, Lehrstuhl für Statik, Technische Universität München, 2009
- ↑ Dieringer, F.: Numerical Methods for the Design and Analysis of Tensile Structures, Lehrstuhl für Statik, Technische Universität München, 2014
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |