Users:Structural Optimization/Response Functions/Mass
Contents |
General Description
Short Info
This response function controls the mass of a finite element system. The value of this response function represents the overall system mass M of all elements computed by summation of all element masses mi.
- M = ∑i mi
Input Parameters
| Block headline | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| OPT-RESPONSE_FCT | int : MASS | Function ID and type mechanical problem. |
| Common compulsory parameters | ||
| ETA | real | Finite difference disturbance for sensitivity analysis |
| GRAD | DIRECT, ADJOINT | Method of gradient computation |
| SA | GLOBAL_FD, SEMI_ANALYTIC, EXACT_SEMI_ANALYTIC, ANALYTIC | Method of derivative computations inside sensitivity analysis |
| FDA | FOREWARD, CENTRAL, BACKWARD | Method of finite difference approximation (if neccessary for the chosen sensitivity analysis method) |
| DESVAR | OPT-VAR vector of integers | Design variables that are considered in the sensitivity analysis of this response function |
| Common optional parameters | ||
| WEIGHT | real, 1.0* | The weighting factor for this response function in multi-objective optimization |
| ANALYSIS | PC-ANALYSIS int | ID of the underlying analysis |
| Specific parameters | ||
| DOMAIN | EL-DOMAIN int | ID of system domain |
| Common Compulsory Parameters for Constraints | ||
| Parameter | Values, Default(*) | Description |
| REL_LIMIT | real | Relative limit for constraint, depending on the actual value. |
| ABS_LIMIT | real | Absolute limit for constraint. Only one limit can be defined for a constraint. |
| CONSTRAINT_TYPE | INEQUALITY_LT, INEQUALITY_GT, EQUALITY | Type of constraint |
| Common Optional Parameters for Constraints | ||
| REL_TOLERANCE | real, 0* | Upper relative limit until which an inactive constraint is concidered as an active one |
| LAMBDA_ABS_MAX | real, 1/cepsilon* | Upper limit for lagrangian multiplier |
Example of a Complete Input Block
OPT-RESPONSE_FCT 1 : MASS ! -- basic stuff WEIGHT=1.0 ETA=1e-06 GRAD=ADJOINT SA=SEMI_ANALYTIC FDA=FOREWARD DESVAR=OPT-VAR 1,2,3,4,5,6 ! -- response function dependant parameters DOMAIN = EL-DOMAIN 1 ! -- constraint parameters ABS_LIMIT = 1-e3 REL_TOLERANCE = 0.1 CONSTRAINT_TYPE = INEQUALITY_LT LAMBDA_ABS_MAX = 20
Examples
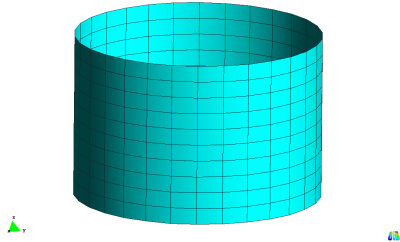
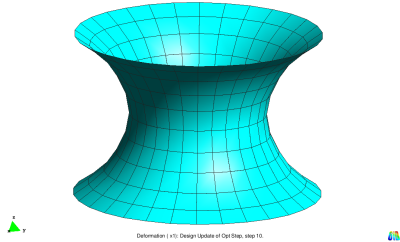
Catenoid
This example considers the mass minimization of a simple catenoid structure. A catenoid can be designed by rotation of the catenary curve[1]. Due to the constant density and thickness it is equivalent to the pure mathematical minimal surface problem. The catenoid as a minimal surface was found by Leonard Euler [2] in 1744. Another principle to compute minimal surfaces is the Formfinding with isotropic pre-stress fields.
Scherkian Minimal Surface
A second example shows another famous minimal surface, namely the so called Scherkian minimal surface[3]. It was found by Heinrich Ferdinand Scherk[4] in 1835.
References
- ↑ http://en.wikipedia.org/wiki/Catenary
- ↑ http://de.wikipedia.org/wiki/Leonhard_Euler
- ↑ http://de.wikipedia.org/wiki/Minimalfl%C3%A4che#Die_Minimalfl.C3.A4che_von_H._F._Scherk
- ↑ http://de.wikipedia.org/wiki/Heinrich_Ferdinand_Scherk
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |