Users:Structural Optimization/Response Functions/Eigenvalue
Contents |
General Description
Short Info
In contrast to the Kreisselmeier-Steinhauser approach this response function only considers one single eigenvalue and the corresponding eigenmode of the eigen dynmaic problem. As therefore the internal weighting becomes needless, this function can be described shortly.
This response function also assumes that the eigenvalue has to be maximized.
Input Parameters
| Block headline | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| OPT-RESPONSE_FCT | int : EIGENVALUE_DYN | Function ID and response function type. |
| Common compulsory parameters | ||
| ETA | real | Finite difference disturbance for sensitivity analysis |
| GRAD | DIRECT, ADJOINT | Method of gradient computation |
| SA | GLOBAL_FD, SEMI_ANALYTIC, EXACT_SEMI_ANALYTIC, ANALYTIC | Method of derivative computations inside sensitivity analysis |
| FDA | FOREWARD, CENTRAL, BACKWARD | Method of finite difference approximation (if neccessary for the chosen sensitivity analysis method) |
| DESVAR | OPT-VAR vector of integers | Design variables that are considered in the sensitivity analysis of this response function |
| Common optional parameters | ||
| WEIGHT | real, 1.0* | The weighting factor for this response function in multi-objective optimization |
| ANALYSIS | PC-ANALYSIS int | ID of the underlying analysis |
| Specific parameters | ||
| NUM_EIGENVALUE | int | Number of eigenvalue to be considered. NUM_VALUE has to be smaller or equal the NUM_ROOT flag inside the eigenvalue analysis. |
| Common Compulsory Parameters for Constraints | ||
| Parameter | Values, Default(*) | Description |
| REL_LIMIT | real | Relative limit for constraint, depending on the actual value. |
| ABS_LIMIT | real | Absolute limit for constraint. Only one limit can be defined for a constraint. |
| CONSTRAINT_TYPE | INEQUALITY_LT, INEQUALITY_GT, EQUALITY | Type of constraint |
| Common Optional Parameters for Constraints | ||
| REL_TOLERANCE | real, 0* | Upper relative limit until which an inactive constraint is concidered as an active one |
| LAMBDA_ABS_MAX | real, 1/cepsilon* | Upper limit for lagrangian multiplier |
Example of a Complete Input Block
OPT-RESPONSE_FCT 1 : EIGENVALUE_DYN WEIGHT=1.0 ANALYSIS=PC-ANALYSIS 1 ETA=1e-06 GRAD=ADJOINT SA=SEMI_ANALYTIC FDA=FOREWARD DESVAR=OPT-VAR 1 ! -- response function dependant parameters NUM_EIGENVALUE = 1 ! -- constraint parameters REL_LIMIT = 1.1 REL_TOLERANCE = 0.1 CONSTRAINT_TYPE = INEQUALITY_LT LAMBDA_ABS_MAX = 20
A complete test example
Model description
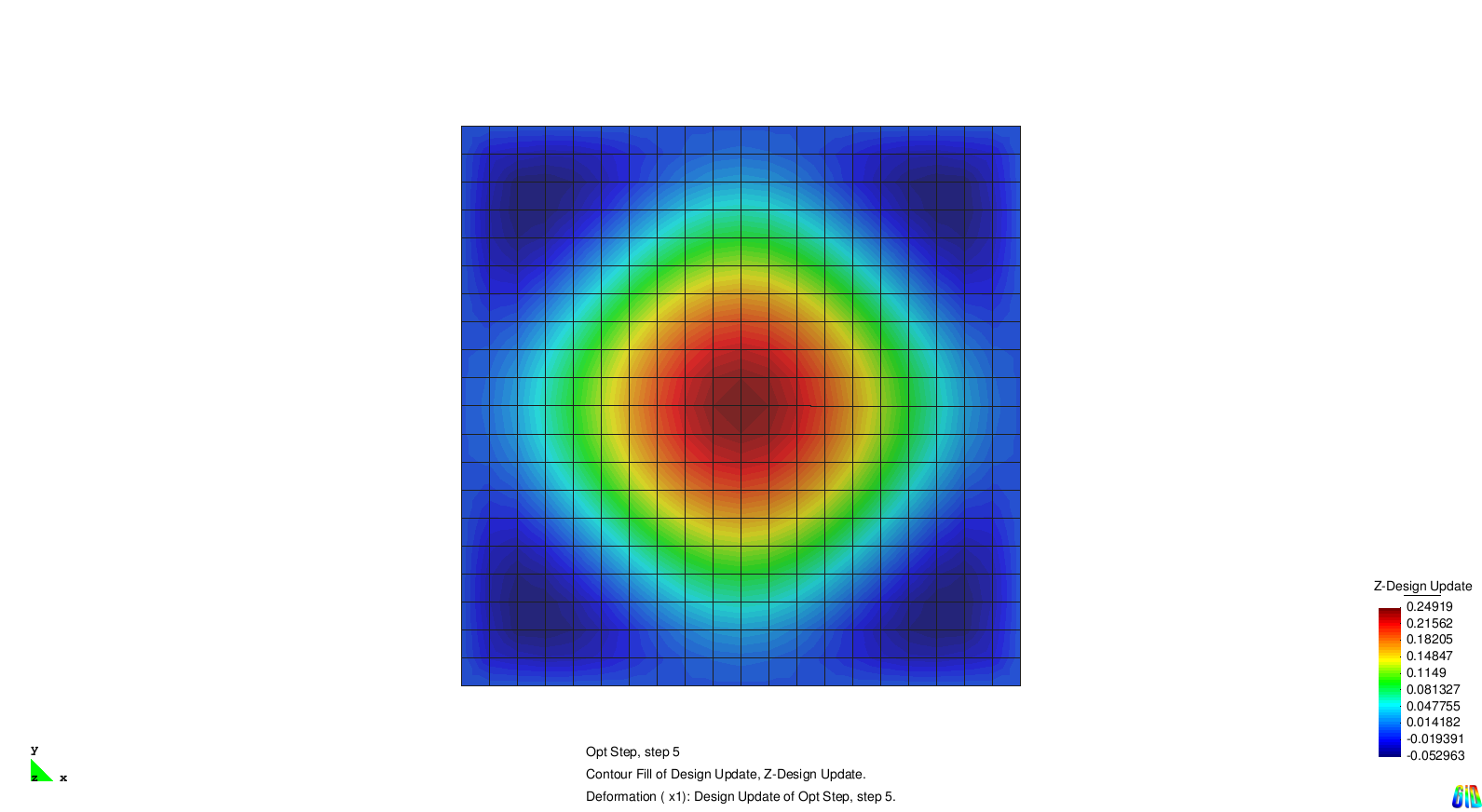
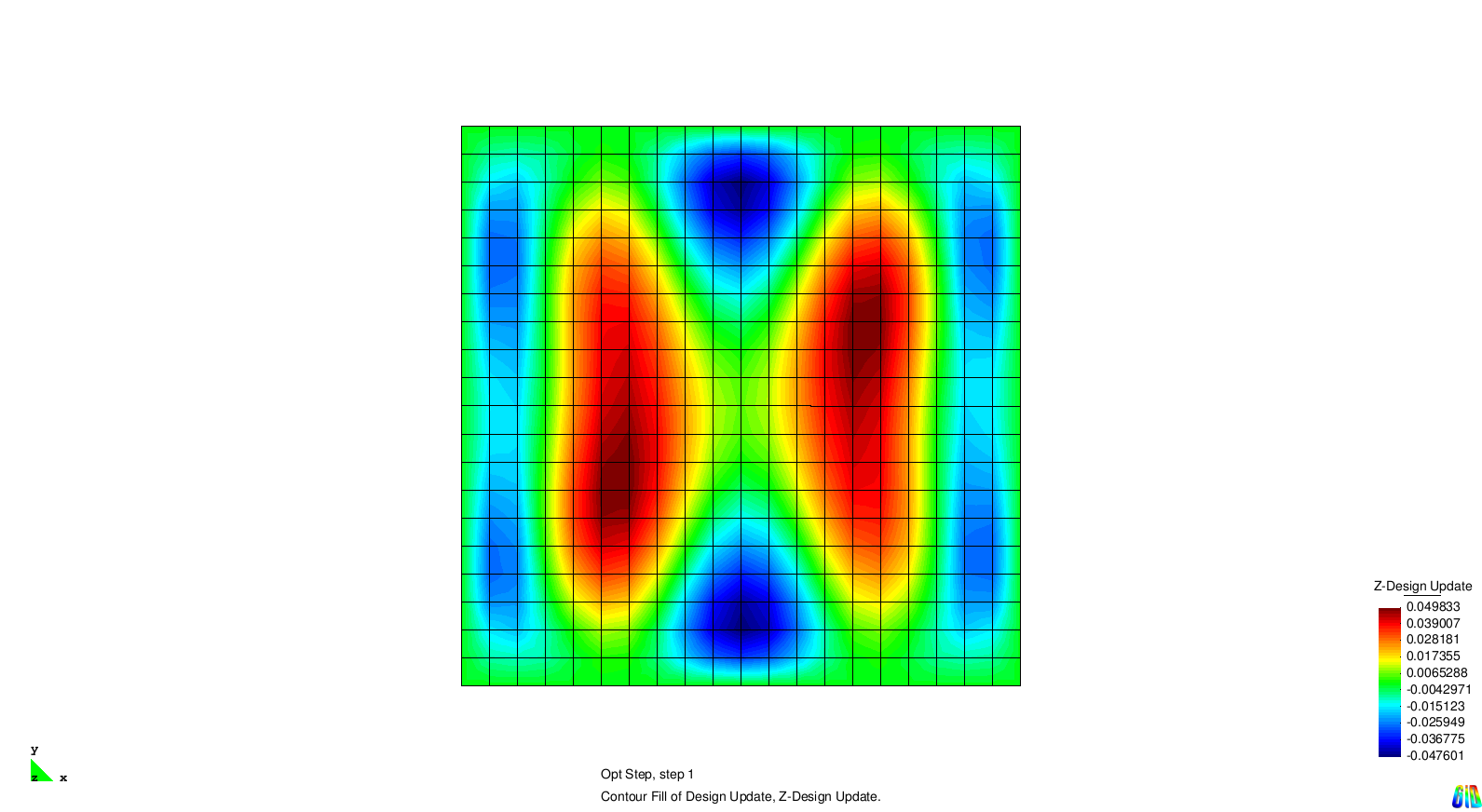
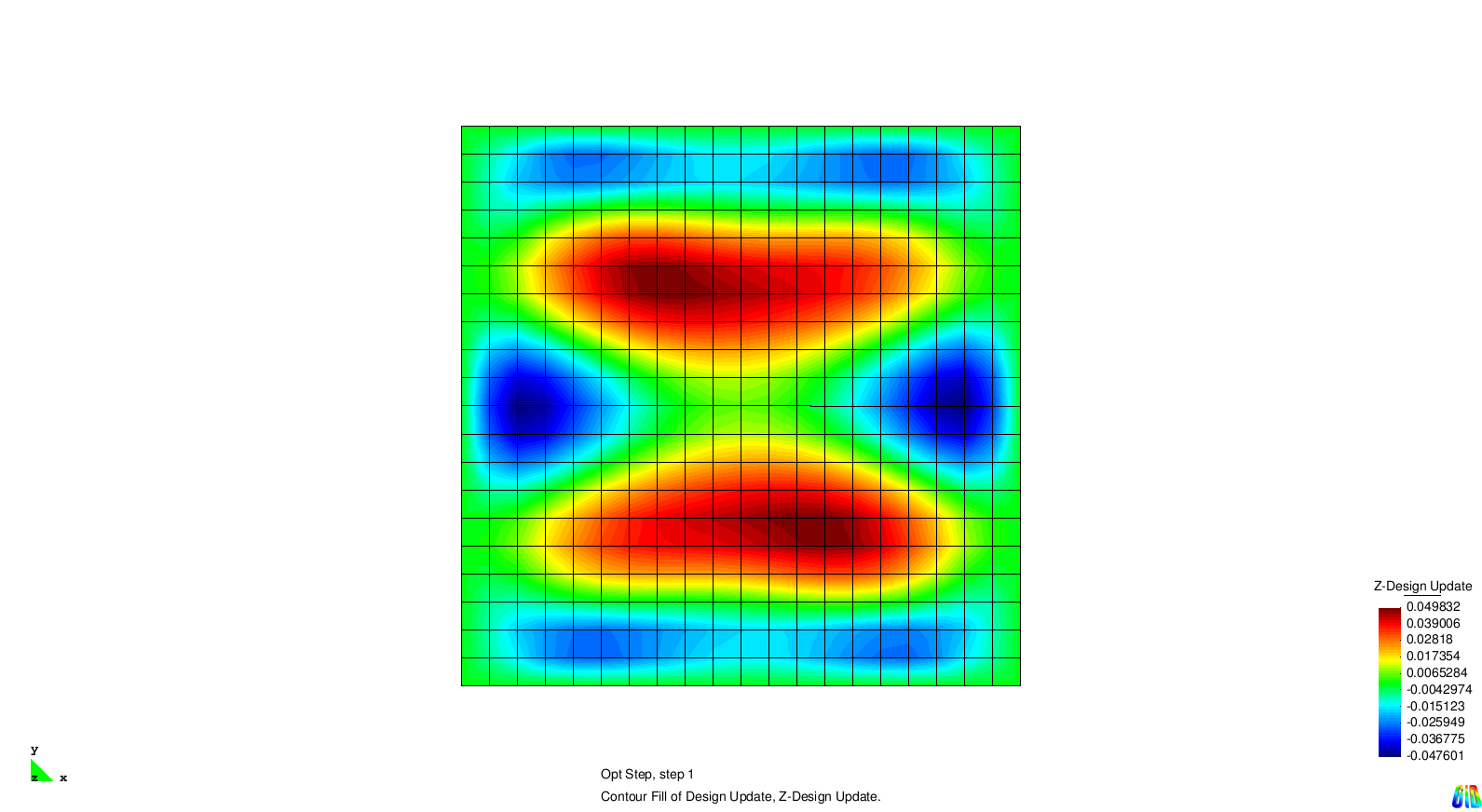
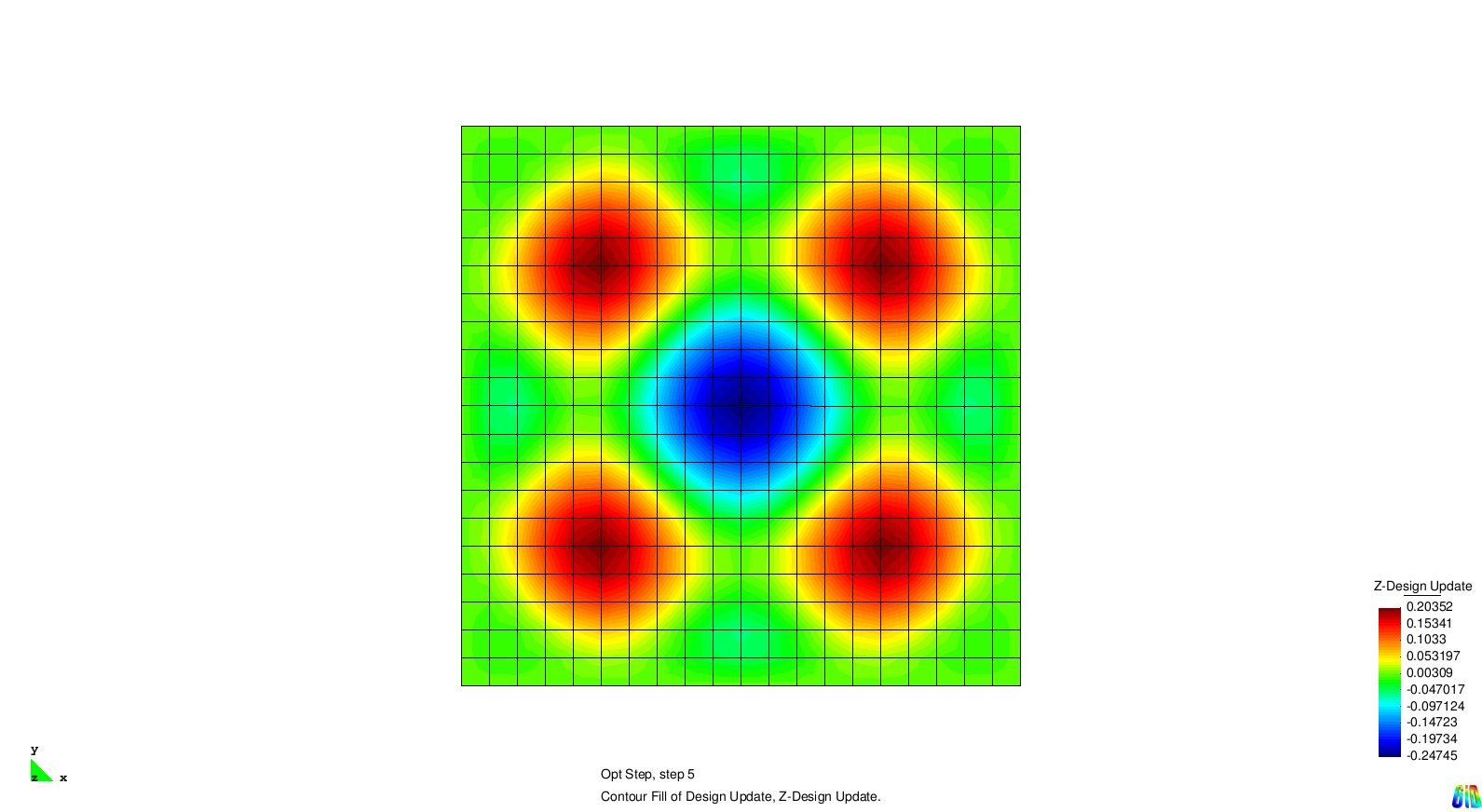
The test example for single eigenvalue optimization is a squared and Navier supported plate. The first four eigenvalues are considered and for each of them an optimization is performed. In the next section we examine the different results.
The following animation illustrates the eigenmodes of the plate.
Input File
Here the full input file can be downloaded.
Documented Results
The results show the expected behaviour. Each solution generates stiffness towards a certain eigenmode. As the modes two and three are symmetric it is not surprising that the design updates are symmetric, too.
References
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |