Users:General FEM Analysis/Analyses Reference/Dynamic Analysis

From Carat++ Public Wiki
< Users:General FEM Analysis | Analyses Reference(Difference between revisions)
Jump to: navigation, search
(→Parameter Description)
 
(22 intermediate revisions by 2 users not shown)
Line 4: Line 4:
  
 
The dynamic analysis is used to analyze the time-dependent or transient behavior of structures. There exist various analysis types with different time integration algorithms and geometric linear and nonlinear formulations to cover small and large structural displacements.
 
The dynamic analysis is used to analyze the time-dependent or transient behavior of structures. There exist various analysis types with different time integration algorithms and geometric linear and nonlinear formulations to cover small and large structural displacements.
 +
 +
  
 
=== Discretization in Space ===
 
=== Discretization in Space ===
Line 12: Line 14:
  
 
with '''M''' as the mass matrix, '''C''' as the damping matrix, '''K''' as the linear stiffness matrix and '''f''' as the external and time-dependent force vector. It has to be noted, that the unknown variables are time-dependent.
 
with '''M''' as the mass matrix, '''C''' as the damping matrix, '''K''' as the linear stiffness matrix and '''f''' as the external and time-dependent force vector. It has to be noted, that the unknown variables are time-dependent.
 +
  
 
=== Discretization in Time ===
 
=== Discretization in Time ===
Line 20: Line 23:
  
 
This is an equation system with ndof equations, but 3 x ndof unknowns.  
 
This is an equation system with ndof equations, but 3 x ndof unknowns.  
 +
  
 
=== Linear Equation System ===
 
=== Linear Equation System ===
Line 28: Line 32:
  
 
This system is solved in every timestep. All terms on the right hand side are already known and the system can be solved for the unknown displacements '''d<sub>n+1</sub>'''. After this, the corresponding velocity and acceleration are determined by backsubstitution.
 
This system is solved in every timestep. All terms on the right hand side are already known and the system can be solved for the unknown displacements '''d<sub>n+1</sub>'''. After this, the corresponding velocity and acceleration are determined by backsubstitution.
 +
  
 
=== Time Integration Methods ===
 
=== Time Integration Methods ===
Line 35: Line 40:
 
*Generalized-alpha method.
 
*Generalized-alpha method.
  
−
The Newmark-beta method uses two control parameters, '''β''' and '''γ'''. The choice of these parameters influences the accuracy and stability of the algorithm. Accuracy of 2nd order is given for '''β=0.25''' and '''γ=0.5'''. Dissipation of higher frequencies is reached for '''γ≥0.5''', but only 1st order accuracy is given. Uncoditional stability is given for '''2β≥γ≥0.5'''.
+
The Newmark-beta method uses two control parameters, '''β''' and '''γ'''. The choice of these parameters influences the accuracy and stability of the algorithm. Accuracy of 2nd order is given for '''β=0.25''' and '''γ=0.5'''. Dissipation of higher frequencies is reached for '''γ≥0.5''', but the accuracy is diminished to 1st order. Unconditional stability is guaranteed for a combination that ensures '''2β≥γ≥0.5'''. More information can be found in the corresponding literature, e.g. Bathe's FE book<ref name="Bathe2001">Bathe, K.J.:Finite-Elemente-Methoden, Springer Verlag, 2001</ref>
  
 +
The Generalized-alpha method is based on the Newmark-beta method, but the equilibrium condition is formulated between two timesteps by linear blending. It uses four control parameters, '''β''' and '''γ''' from the Newmark-beta method and additionally the two linear shift-parameters '''α<sub>m</sub>''' and '''α<sub>f</sub>'''. The advantage of the Generalized-alpha method is to ensure 2nd order accuracy with controllable damping of higher frequency modes. The control parameters depend on the wanted damping of the higher frequencies, which is described by the spectral radius '''ρ<sub>∞</sub>'''. For '''ρ<sub>∞</sub>=1.0''' no damping occurs, for '''ρ<sub>∞</sub><1.0''' higher frequencies are damped. An overview on parameter combinations is given in the following table. Other values can be found in the corresponding literature, e.g. the dissertation of Detlef Kuhl<ref name="Kuhl1996">Kuhl, D.: Stabile Zeitintegrationsalgorithmen in der nichtlinearen Elastodynamik dünnwandiger Tragwerke, Dissertation, Bericht Nr. 22, Institut für Baustatik, Universität Stuttgart, 1996</ref> or Thomas Gallinger<ref name="Gallinger2010">Gallinger, T.G.: Effiziente Algorithmen zur partitionierten Lösung stark gekoppelter Probleme der Fluid-Struktur-Wechselwirkung, Dissertation, Lehrstuhl für Statik, Technische Universität München, 2010</ref>
  
−
=== Geometric Linearity and Nonlinearity ===
+
{| border="1" cellpadding="5" cellspacing="0"
 +
|colspan="5" style="background:#efefef;"| Parameter Combination for Generalized-Alpha Method
 +
|-
 +
!Spectral radius ρ<sub>∞</sub>
 +
!β
 +
!γ
 +
!α<sub>m</sub>
 +
!α<sub>f</sub>
 +
|-
 +
!1.0
 +
|0.250
 +
|0.500
 +
|0.500
 +
|0.500
 +
|-
  
 +
!0.9
 +
|0.277
 +
|0.553
 +
|0.421
 +
|0.474
 +
|-
  
−
=== Rayleigh Damping ===
+
!0.8
 +
|0.309
 +
|0.611
 +
|0.333
 +
|0.444
 +
|-
 +
|}
  
  
−
=== Initial Load ===
 
  
 +
=== Geometric Linearity and Nonlinearity ===
  
 +
Choosing the algorithm decides whether a geometric linear or nonlinear formulation is used. Whereas the geometric linear formulation allows a solution within one iteration per timestep, the nonlinear formulation is based on a residuum formulation, a linearization and an iterative Newton method. So for a nonlinear analysis, in addition the maximum number of Newton iterations and the maximum norm of the residual force vector for the convergence proof has to be specified.
  
−
=== Restart Functionaliy ===
 
  
 +
=== Rayleigh Damping ===
  
−
A nonlinear problem is formulated by the equation '''r''' = '''f'''_int('''u''') - λ * '''f'''_ext('''u''') where '''r''' specifies the residual vector and '''f'''_int and '''f'''_ext define the internal and external forces respectively. In general, the internal forces as well as the external forces depend on the actual displacement field '''u'''. Thus, the equation is nonlinear with respect to the a priori unknown equilibrium displacements. The parameter λ specifies a scaling parameter for the external load. Usually this parameter is controlled by a load curve which specifies λ as a function of the pseudo time t. The slope of this load curve must be small enough such that convergence is possible in each step. Whenever a nonlinear analysis has convergence problems it is appropriate to reduce the slope of this load curve and calculate more time steps.
+
The damping term '''C v''' is velocity proportional and depends on the damping matrix '''C''', which represents the influence of internal friction. This influence is typically not covered within the classical finite element derivation, but there exist other methods to determine a damping matrix. In Carat++ the so-called Rayleigh damping is implemented, which determines the damping matrix as a linear combination of the mass and stiffness matrix: '''C = α<sub>1</sub>M + α<sub>2</sub>K'''. The linear coefficients '''α<sub>1</sub>''' and '''α<sub>2</sub>''' are problem-dependent and can be determined from experiments.  
  
−
At the equilibrium point the internal forces are equal to the external forces and the residual vector is equal to zero. The above specified nonlinear problem is linearized for the actual displacement state and solved by a Newton-Raphson scheme where the residual vector is used to compute incremental displacements by '''K'''_t '''u'''_inc = '''r'''. Here the tangential stiffness matrix is specified by '''K'''_t whereas '''u'''_inc denotes the incremental displacements.
 
  
−
=== Path Following Methods ===
+
=== Loading and Load Curves ===
−
The iterative solution of the nonlinear problem requires path following methods. The most simple path following method is a pure '''Load Control'''. Here the parameter ''lambda'' is increased according to the specified load curve. This allows nonlinear analysis for relatively robust nonlinear problems. But as soon as the structure shows instabilities the load control method usually does not not converge anymore. In this case the '''Arc Length''' method can be applied to compute the equilibrium path. This method controls the so called arc length which is defined as a combination from displacement increment and load increment. In general it is also possible to directly control a specified displacement. But actually this path control method is not available in Carat++. More information about path following methods can be found in the thesis of Reiner Reitinger<ref name="Rei94">Reitinger, R.: Stabilität und Optimierung imperfektionsempfindlicher Tragwerke, Dissertation, Bericht Nr. 17, Institut für Baustatik, Universität Stuttgart, 1994</ref> and Amphon Jarusjarungkiat.
+
  
−
=== Step Length Control ===
+
The external load, which has to be specified, is time-dependent. To handle this in Carat++, one or more load curves have to be defined and combined with nodal and element loads. It is possible to specify e.g. one load curve for self-weight, another load curve for some single nodal loads and a third load curve for wind. The load curves consist of a list of discrete pairs of time and value. At least two time instances have to be specified. Between the time instances linear interpolation is used. Therefore, it is not necessary, that time instances of the load curve and computed times of the dynamic analysis match. It is only necessary, that the computed time interval is covered by all specified load curves.
−
Actually there exist two methods for step length control in Carat++. The most simple method is the fixed step length which computes the whole load displacement path with a constant step length. This procedure is robust but inefficient because a large number of load steps has to be computed. Usually it is more efficient to apply adaptive step length methods. A very robust method was presented by Crisfield and Ramm, c.f. <ref name="Rei94" />. This method specifies the actual step length for the time step ''i'' by the operation ''StepLength_i'' = ''alpha'' * ''StepLength_i-1''. The parameter ''alpha'' is computed by ''(J_d / (J_i-1 * (Nmb_Restarts+1)))^p'' with: ''J_d'' = desired number of equilibrium iterations, ''J_i-1'' = equilibrium iterations of last time step and ''p'' equals the exponent.
+
  
−
<pre>
 
−
Example:  Actual iteration step:                                  i
 
−
          Number of desired equilibrium iterations:                J_d = 8.
 
−
          Number of equilibrium iterations in the last time step:  J_i-1 = 12.
 
−
          Number of restarts:                                      Nmb_Restarts = 0.
 
−
          Exponent:                                                p=1.0.
 
−
          Step length of last step:                                StepLength_i-1 = 0.2.
 
  
−
          alpha = ( 8 / (12*(0+1)))^(1.0) = (8 / 12)^(1.0) = 2/3.
+
=== Initial Load ===
−
          StepLength_i = 2/3 * 0.2 = 0.1333.
+
  
−
</pre>
+
An Initial Load exists, if the external loading at start time is not equal to zero. This may be case, if e.g. the loading consists of constant self-weight and a time-varying nodal load. If this is the case, an initial static solution is carried out and used as starting point for the dynamic analysis.
  
−
Thus, if the number of equilibrium iterations is larger than a desired value the step length is decreased for the next time step. If the number of equilibrium iterations is smaller than a desired value the step length is increased for the next time step. The exponent ''p'' can be used to manipulate the update speed. It should be used with care.
 
  
−
=== Simultaneous Eigenvalue Analysis ===
+
=== Restart Functionaliy ===
−
Reaching critical points of the load displacement path (limit points, bifurcation points, ...) requires special investigations. A simultaneous eigenvalue analysis solving the problem ('''K'''_t - ''eigenvalue'' * '''I''') '''phi''' = '''0''' allows for approximation of the load factor at the next critical point ''lambda''_k. Whenever a critical point is reached the above equations yields to a zero eigenvalue. Extrapolating the current load factor according to the eigenvalue allows for good approximations of the critical load.
+
 
 +
A Restart Functionality is implemented in Carat++, which allows to continue a dynamic computation from a certain time instance. It is useful in some cases:
 +
*On cluster computing systems, typically computing time restrictions exist. The restart functionality allows to continue the computation from an already reached time instance.
 +
*Very long and nonlinear computations with large displacements may show convergence problems and diverge. The restart functionality allows to perform a restart from an already computed level and adapt the solution approach, e.g. by diminishing the time step size, changing the time integration algorithm or introducing
 +
The restart functionality consists of two parts. First, information necessary for a restart is written with a certain frequency into files with a certain name. Different time instances are stored to be able to restart not only from the last level, but also from an earlier level. Second, if a restart is performed, the starting time of the restart has to be specified. There will always exist two restartfiles, which are filled alternating.  
  
−
=== Imperfect Designs ===
 
−
Many structures subjected to large compression loading are sensitive to geometrical imperfections. Unfortunately the shape of the imperfection is a priori unknown but mostly some information about tolerances exist. In the nonlinear analysis the imperfection shapes can be computed as sum of several  normalized eigenmodes. The final imperfection mode is then scaled by the specified tolerance. This operation can be expressed by d'''x'''_imp = tol * (sum_i '''phi'''_i). After computation of the imperfection mode, the geometry of the structure is modified and the nonlinear analysis starts with the imperfect geometry.
 
  
 
== Input Parameters ==
 
== Input Parameters ==
Line 87: Line 110:
  
 
{| border="1" cellpadding="3" cellspacing="0"
 
{| border="1" cellpadding="3" cellspacing="0"
−
|colspan="3" style="background:#efefef;"| Compulsory Parameters
+
|colspan="3" style="background:#efefef;"| Compulsory Paramters
 
|-
 
|-
−
!Parameter
+
!PC-ANALYSIS
−
!Values, Default(*)
+
|''int: DYNAMIC''
−
!Description
+
|Keyword of dynamic analysis with analysis ID
 
|-
 
|-
−
!PC-ANALYSIS
+
!SOLVER
−
|''int'' : STA_GEO_NONLIN
+
|''PC-SOLVER int''
−
|Keyword of nonlinear analysis with analysis ID
+
|Linking to a linear solver
 
|-
 
|-
−
!PATHCONTROL
+
!STARTTIME
−
|FORCE or ARCLENGTH or DISPLACEMENT
+
|''float''
−
|Definition of path control method. (DISPLACEMENT is actually not available.)
+
|Starttime of simulation
 
|-
 
|-
−
!SOLVER
+
!ENDTIME
−
|PC-SOLVER ''int''
+
|''float''
−
|Linking to a linear solver (direct or iterative)
+
|Endtime of simulation
 +
|-
 +
!TIMESTEP
 +
|''float''
 +
|Timestep of simulation
 
|-
 
|-
 
!OUTPUT
 
!OUTPUT
−
|PC-OUT ''int''
+
|''PC-OUT int''
−
|Linking to output objects (specifies the type of output format, e.g. GiD)
+
|Link to [[Users:General FEM Analysis/Data Output|output object]]
 
|-
 
|-
 
!COMPCASE
 
!COMPCASE
−
|LD-COM ''int''
+
|''LD-COM int''
−
|Linking to computation case object which specify the boundary conditions (loading and supports). Only a single computation case is allowed.
+
|Link to computation case
 
|-
 
|-
 
!DOMAIN
 
!DOMAIN
−
|EL-DOMAIN ''int''
+
|''EL-DOMAIN int''
−
|Linking to the domain the analysis should work on
+
|Link to domain object
 
|-
 
|-
−
!NUM_STEP
+
!ALGORITHM
−
|''int''
+
|''NEWMARK_LIN or NEWMARK_NLN or GENALPHA_LIN or GENALPHA_NLN''
−
|Number of time steps that have to be calculated
+
|choose the time integration algorithm and linear or nonlinear gemoetry
 +
|-
 +
!BETA
 +
|''float''
 +
|Parameter β in Newmark-beta and Generalized-alpha method
 +
|-
 +
!GAMMA
 +
|''float''
 +
|Parameter γ in Newmark-beta and Generalized-alpha method
 +
|-
 +
!ALPHA_M
 +
|''float''
 +
|Parameter α<sub>m</sub> in Generalized-alpha method
 +
|-
 +
!ALPHA_F
 +
|''float''
 +
|Parameter α<sub>f</sub> in Generalized-alpha method
 
|-
 
|-
 
!MAX_ITER_EQUILIBRIUM
 
!MAX_ITER_EQUILIBRIUM
 
|''int''
 
|''int''
−
|Maximum number of equilibrium iterations that are allowed. 
+
|Maximum number of Newton iterations to reach convergence - only for geometric nonlinear analysis
 
|-
 
|-
 
!EQUILIBRIUM_ACCURACY
 
!EQUILIBRIUM_ACCURACY
 
|''float''
 
|''float''
−
|Equilibrium accuracy that has to be reached for convergence. The convergence is checked with the L2 norm of the incremental displacements.
+
|L2-norm of the residual as convergence proof - only for geometric nonlinear analysis
 
|-
 
|-
−
!CURVE
+
|colspan="3" style="background:#efefef;"| Optional Parameters for Rayleigh Damping
−
|LD-CURVE ''int''
+
−
|Linking to the load curve.
+
 
|-
 
|-
−
|colspan="3" style="background:#efefef;"| Optional Parameters
+
!DAMPING
 +
|''0 or 1''
 +
|Add Rayleigh damping matrix to system
 
|-
 
|-
−
!TRACED_NODE
+
!A1
−
|''int''
+
|''float''
−
|Node ID of traced node. Used for screen and log file output.
+
|Parameter α<sub>1</sub>
 
|-
 
|-
−
!TRACED_NODAL_DOF
+
!A2
−
|''dof type''
+
|''float''
−
|DOF type of node TRACED_NODE that has to be traced (DISP_X, DISP_Y, DISP_Z, ...).
+
|Parameter α<sub>3</sub>
 
|-
 
|-
−
!STEP_LENGTH_CONTROL
+
|colspan="3" style="background:#efefef;"| Optional Parameters for Restart
−
|FIXED or CRISFIELD_RAMM
+
−
|Type of step length control algorithm (for ARCLENGTH method). FIXED specifies a constant step size where the desired step size is defined by the parameter STEP_LENGTH_CONTROL_REALS. CRISFIELD_RAMM specifies an adaptive method according to Crisfield and Ramm, c.f. <ref name="Rei94" />. In this case the parameter  STEP_LENGTH_CONTROL_INTS = ''int'' specifies the number of restarts that are allowed. The other necessary parameters are specified by STEP_LENGTH_CONTROL_REALS. See the example below. 
+
 
|-
 
|-
−
!STEP_LENGTH_CONTROL_REALS
+
!RESTARTRUN
−
|''float'', ''float'', ...
+
|''0 or 1''
−
|respective number of floats for step length control algorithm
+
|Perform restart from STARTTIME, read restart information from file with prefix RESTARTFILEPREFIX
 
|-
 
|-
−
!STEP_LENGTH_CONTROL_INTS
+
!RESTARTOUTPUT
−
|''int'', ''int'', ...
+
|''0 or 1''
−
|respective number of integers for step length control algorithm
+
|Write restart info to file with prefix RESTARTFILEPREFIX every RESTARTFREQUENCY steps
 
|-
 
|-
−
!SIMULTANEOUS_EIGENVALUE_ANALYSIS
+
!RESTARTFREQUENCY
−
|1 or 0
+
|''int''
−
|flag to specify if a simultaneous eigenvalue analysis should be performed, 0 - no eigenvalue analysis, 1 - perform eigenvalue analysis. This flag requires definition of parameter EIGEN_SOLVER.
+
|Frequency of timesteps to write restart info to RESTARTFILEPREFIX
 
|-
 
|-
−
!EIGEN_SOLVER
+
!RESTARTFILEPREFIX
−
|PC-SOLVER ''int''
+
|''string''
−
|Linking to an eigenvalue solver
+
|Write restart info to or read from files with names RESTARTFILEPREFIX.restart_1 and .restart_2
 
|-
 
|-
−
!IMPERFECTION_MODES
+
!RESTARTINFOINSTANCES
−
|''int'', ''int'', ''int'', ...
+
|''int''
−
|specifies which eigen modes should be summarized to the imperfection mode. Computation of imperfect design requires definition of parameter EIGEN_SOLVER.
+
|Keep restart information from RESTARTINFOINSTANCES in files, until info is overwritten
 
|-
 
|-
−
!IMPERFECTION_SIZE
 
−
|''float''
 
−
|specifies the size of the imperfection mode.
 
 
|}
 
|}
−
 
  
 
=== Example of a Complete Input Block ===
 
=== Example of a Complete Input Block ===
 +
 +
<pre>
 +
PC-ANALYSIS 2: DYNAMIC
 +
  SOLVER = PC-SOLVER 1
 +
  STARTTIME = 0.0
 +
  ENDTIME  = 2.0
 +
  TIMESTEP  = 0.0001
 +
  ALGORITHM = NEWMARK_NLN
 +
  BETA    = 0.25
 +
  GAMMA    = 0.50
 +
  ALPHA_M  = 0.50
 +
  ALPHA_F  = 0.50
 +
  OUTPUT  = PC-OUT 1
 +
  COMPCASE = LD-COM 1
 +
  DOMAIN  = EL-DOMAIN 1
 +
  MAX_ITER_EQUILIBRIUM = 25
 +
  EQUILIBRIUM_ACCURACY = 0.00000001
 +
  DAMPING = 1
 +
  A1 = 2.709094
 +
  A2 = 0.000441
 +
  RESTARTRUN = 0
 +
  RESTARTOUTPUT = 1
 +
  RESTARTFREQUENCY = 10
 +
  RESTARTFILEPREFIX = restartfile
 +
  RESTARTINFOINSTANCES = 3
 +
</pre>
 +
 +
 +
=== Example of a Load Curve ===
 +
 +
<pre>
 +
LD-CURVE 1 TYPE=DISCRETE
 +
TIME=0.000  VAL=0.000
 +
TIME=0.500  VAL=1.000
 +
TIME=2.000  VAL=9.000
 +
</pre>
 +
 +
 +
 +
== Example ==
 +
 +
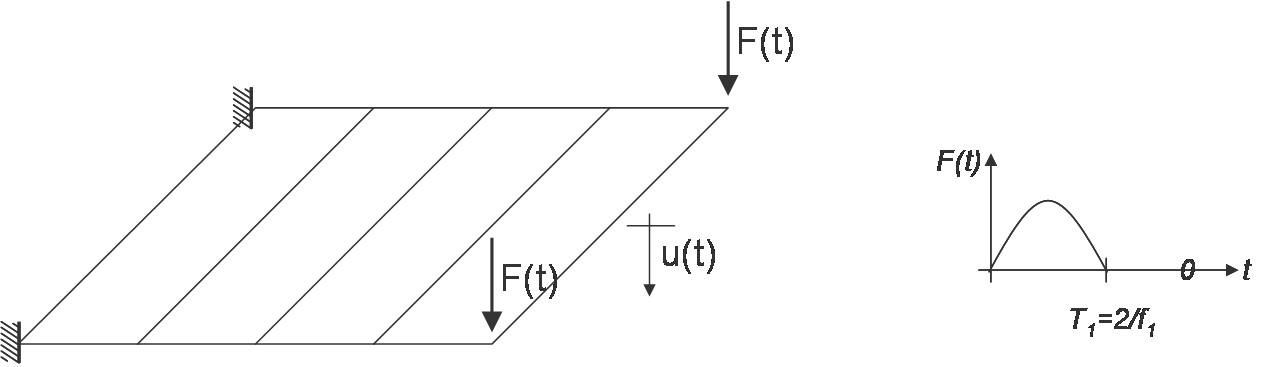
The following simple example shows a dynamic and geometric nonlinear analysis of a cantilever arm using the onlinear Newmark-beta method. The respective input file can be found in the SVN repository under
 +
<pre>
 +
carat20/examples/benchmark_examples/analyses/dynamic_nonlinear_newmark_shell8_I/dynamic_nonlinear_newmark_shell8.txt
 +
</pre>
 +
 +
The cantilever structure is modeled by four shell8-elements. Two single loads are applied on the tip perpendicular to the system area. The system is excited by a half-sinus.
 +
 +
{|
 +
|[[File:CantileverStructure.png‎|thumb|up|750px|Cantilever structure discretized with shell8-Elements]]
 +
|}
 +
 +
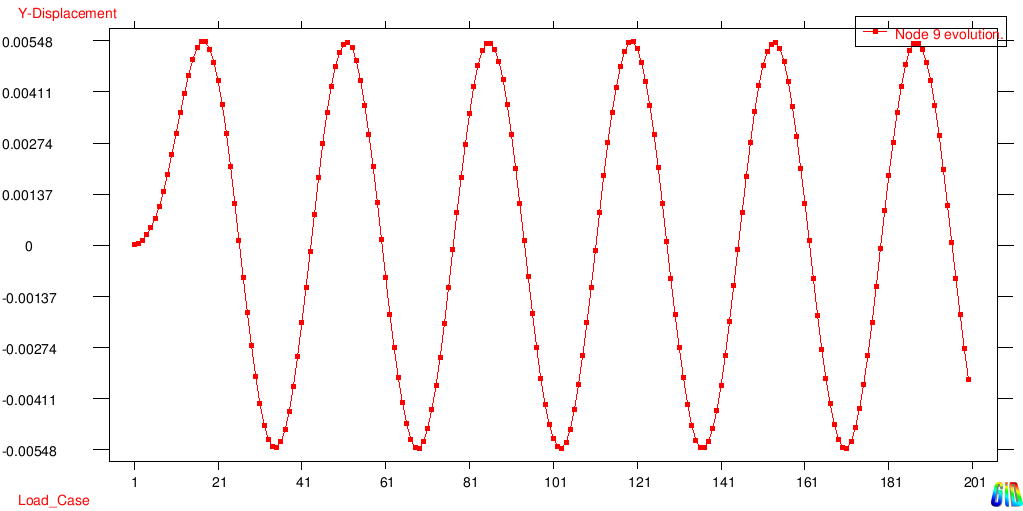
The system shows an oscillation in the first Eigenform. The displacement versus timestep diagram is given in the figure below.
 +
 +
{|
 +
|[[File:DispVsIter.png‎|thumb|up|750px|Displacement Versus Timesteps (u(t)) at the tip of the Cantilever]]
 +
|}
 +
 +
 +
 +
 +
== References ==
 +
 +
<references/>

Latest revision as of 14:15, 18 December 2010


Contents

General Description

The dynamic analysis is used to analyze the time-dependent or transient behavior of structures. There exist various analysis types with different time integration algorithms and geometric linear and nonlinear formulations to cover small and large structural displacements.


Discretization in Space

The unknown variables used to describe the transient behavior of a structure are the displacement d, the velocity v and the acceleration a. The discretization in space by the Finite Element Method (FEM) leads to the general form of the linear equation of motion:

M a(t)+C v(t)+K d(t)=f(t)

with M as the mass matrix, C as the damping matrix, K as the linear stiffness matrix and f as the external and time-dependent force vector. It has to be noted, that the unknown variables are time-dependent.


Discretization in Time

For the discretization in time a time integration algorithm is used. The discretization is done in two steps. First, the examined time period t=[t0, ttot] is subdivided into discrete intervalls [tn, tn+1] and corresponding time steps Δtn=tn+1-tn. Seccond, for the progress of the variables within a timestep certain assumptions are made, depending on the choosen time integration algorithm. The solution is then only computed at discrete times. In Carat++ implicit time integration algorithms are used, which satisfy dynamic equilibrium at time n+1. Now, the system has the form:

M an+1+C vn+1+K dn+1=fn+1

This is an equation system with ndof equations, but 3 x ndof unknowns.


Linear Equation System

The chosen time integration algorithm allows a reduction to ndof equations, so it makes the system solvable. The acceleration and velocity can be formulated depending on the displacements only, so the main variable is the displacement. Using e.g. the Newmark-beta method leads to the following linear equation system:

(1/βΔt2 M + γ/2Δt C + K) dn+1=fn+1 + M(1/βΔt2dn + 1/βΔt vn + ...) +C(-vn- (1-γ)Δt an+...)

This system is solved in every timestep. All terms on the right hand side are already known and the system can be solved for the unknown displacements dn+1. After this, the corresponding velocity and acceleration are determined by backsubstitution.


Time Integration Methods

There are currently two time integration methods implemented:

  • Newmark-beta method,
  • Generalized-alpha method.

The Newmark-beta method uses two control parameters, β and γ. The choice of these parameters influences the accuracy and stability of the algorithm. Accuracy of 2nd order is given for β=0.25 and γ=0.5. Dissipation of higher frequencies is reached for γ≥0.5, but the accuracy is diminished to 1st order. Unconditional stability is guaranteed for a combination that ensures 2β≥γ≥0.5. More information can be found in the corresponding literature, e.g. Bathe's FE book[1]

The Generalized-alpha method is based on the Newmark-beta method, but the equilibrium condition is formulated between two timesteps by linear blending. It uses four control parameters, β and γ from the Newmark-beta method and additionally the two linear shift-parameters αm and αf. The advantage of the Generalized-alpha method is to ensure 2nd order accuracy with controllable damping of higher frequency modes. The control parameters depend on the wanted damping of the higher frequencies, which is described by the spectral radius ρ∞. For ρ∞=1.0 no damping occurs, for ρ∞<1.0 higher frequencies are damped. An overview on parameter combinations is given in the following table. Other values can be found in the corresponding literature, e.g. the dissertation of Detlef Kuhl[2] or Thomas Gallinger[3]

Parameter Combination for Generalized-Alpha Method
Spectral radius ρ∞ β γ αm αf
1.0 0.250 0.500 0.500 0.500
0.9 0.277 0.553 0.421 0.474
0.8 0.309 0.611 0.333 0.444


Geometric Linearity and Nonlinearity

Choosing the algorithm decides whether a geometric linear or nonlinear formulation is used. Whereas the geometric linear formulation allows a solution within one iteration per timestep, the nonlinear formulation is based on a residuum formulation, a linearization and an iterative Newton method. So for a nonlinear analysis, in addition the maximum number of Newton iterations and the maximum norm of the residual force vector for the convergence proof has to be specified.


Rayleigh Damping

The damping term C v is velocity proportional and depends on the damping matrix C, which represents the influence of internal friction. This influence is typically not covered within the classical finite element derivation, but there exist other methods to determine a damping matrix. In Carat++ the so-called Rayleigh damping is implemented, which determines the damping matrix as a linear combination of the mass and stiffness matrix: C = α1M + α2K. The linear coefficients α1 and α2 are problem-dependent and can be determined from experiments.


Loading and Load Curves

The external load, which has to be specified, is time-dependent. To handle this in Carat++, one or more load curves have to be defined and combined with nodal and element loads. It is possible to specify e.g. one load curve for self-weight, another load curve for some single nodal loads and a third load curve for wind. The load curves consist of a list of discrete pairs of time and value. At least two time instances have to be specified. Between the time instances linear interpolation is used. Therefore, it is not necessary, that time instances of the load curve and computed times of the dynamic analysis match. It is only necessary, that the computed time interval is covered by all specified load curves.


Initial Load

An Initial Load exists, if the external loading at start time is not equal to zero. This may be case, if e.g. the loading consists of constant self-weight and a time-varying nodal load. If this is the case, an initial static solution is carried out and used as starting point for the dynamic analysis.


Restart Functionaliy

A Restart Functionality is implemented in Carat++, which allows to continue a dynamic computation from a certain time instance. It is useful in some cases:

  • On cluster computing systems, typically computing time restrictions exist. The restart functionality allows to continue the computation from an already reached time instance.
  • Very long and nonlinear computations with large displacements may show convergence problems and diverge. The restart functionality allows to perform a restart from an already computed level and adapt the solution approach, e.g. by diminishing the time step size, changing the time integration algorithm or introducing

The restart functionality consists of two parts. First, information necessary for a restart is written with a certain frequency into files with a certain name. Different time instances are stored to be able to restart not only from the last level, but also from an earlier level. Second, if a restart is performed, the starting time of the restart has to be specified. There will always exist two restartfiles, which are filled alternating.


Input Parameters

Parameter Description

Compulsory Paramters
PC-ANALYSIS int: DYNAMIC Keyword of dynamic analysis with analysis ID
SOLVER PC-SOLVER int Linking to a linear solver
STARTTIME float Starttime of simulation
ENDTIME float Endtime of simulation
TIMESTEP float Timestep of simulation
OUTPUT PC-OUT int Link to output object
COMPCASE LD-COM int Link to computation case
DOMAIN EL-DOMAIN int Link to domain object
ALGORITHM NEWMARK_LIN or NEWMARK_NLN or GENALPHA_LIN or GENALPHA_NLN choose the time integration algorithm and linear or nonlinear gemoetry
BETA float Parameter β in Newmark-beta and Generalized-alpha method
GAMMA float Parameter γ in Newmark-beta and Generalized-alpha method
ALPHA_M float Parameter αm in Generalized-alpha method
ALPHA_F float Parameter αf in Generalized-alpha method
MAX_ITER_EQUILIBRIUM int Maximum number of Newton iterations to reach convergence - only for geometric nonlinear analysis
EQUILIBRIUM_ACCURACY float L2-norm of the residual as convergence proof - only for geometric nonlinear analysis
Optional Parameters for Rayleigh Damping
DAMPING 0 or 1 Add Rayleigh damping matrix to system
A1 float Parameter α1
A2 float Parameter α3
Optional Parameters for Restart
RESTARTRUN 0 or 1 Perform restart from STARTTIME, read restart information from file with prefix RESTARTFILEPREFIX
RESTARTOUTPUT 0 or 1 Write restart info to file with prefix RESTARTFILEPREFIX every RESTARTFREQUENCY steps
RESTARTFREQUENCY int Frequency of timesteps to write restart info to RESTARTFILEPREFIX
RESTARTFILEPREFIX string Write restart info to or read from files with names RESTARTFILEPREFIX.restart_1 and .restart_2
RESTARTINFOINSTANCES int Keep restart information from RESTARTINFOINSTANCES in files, until info is overwritten

Example of a Complete Input Block 

PC-ANALYSIS 2: DYNAMIC
  SOLVER = PC-SOLVER 1
  STARTTIME = 0.0
  ENDTIME   = 2.0
  TIMESTEP  = 0.0001
  ALGORITHM = NEWMARK_NLN
  BETA     = 0.25
  GAMMA    = 0.50
  ALPHA_M  = 0.50
  ALPHA_F  = 0.50
  OUTPUT   = PC-OUT 1
  COMPCASE = LD-COM 1
  DOMAIN   = EL-DOMAIN 1
  MAX_ITER_EQUILIBRIUM = 25
  EQUILIBRIUM_ACCURACY = 0.00000001
  DAMPING = 1
  A1 = 2.709094
  A2 = 0.000441
  RESTARTRUN = 0
  RESTARTOUTPUT = 1
  RESTARTFREQUENCY = 10
  RESTARTFILEPREFIX = restartfile
  RESTARTINFOINSTANCES = 3


Example of a Load Curve 

LD-CURVE 1 TYPE=DISCRETE
 TIME=0.000   VAL=0.000
 TIME=0.500   VAL=1.000
 TIME=2.000   VAL=9.000


Example

The following simple example shows a dynamic and geometric nonlinear analysis of a cantilever arm using the onlinear Newmark-beta method. The respective input file can be found in the SVN repository under 

carat20/examples/benchmark_examples/analyses/dynamic_nonlinear_newmark_shell8_I/dynamic_nonlinear_newmark_shell8.txt

The cantilever structure is modeled by four shell8-elements. Two single loads are applied on the tip perpendicular to the system area. The system is excited by a half-sinus.

Cantilever structure discretized with shell8-Elements

The system shows an oscillation in the first Eigenform. The displacement versus timestep diagram is given in the figure below.

Displacement Versus Timesteps (u(t)) at the tip of the Cantilever



References

  1. ↑ Bathe, K.J.:Finite-Elemente-Methoden, Springer Verlag, 2001
  2. ↑ Kuhl, D.: Stabile Zeitintegrationsalgorithmen in der nichtlinearen Elastodynamik dünnwandiger Tragwerke, Dissertation, Bericht Nr. 22, Institut für Baustatik, Universität Stuttgart, 1996
  3. ↑ Gallinger, T.G.: Effiziente Algorithmen zur partitionierten Lösung stark gekoppelter Probleme der Fluid-Struktur-Wechselwirkung, Dissertation, Lehrstuhl für Statik, Technische Universität München, 2010




Whos here now:   Members 0   Guests 0   Bots & Crawlers 1
 
Retrieved from "http://carat.st.bv.tum.de/caratuserswiki/index.php/Users:General_FEM_Analysis/Analyses_Reference/Dynamic_Analysis"
Personal tools
Content for Users
Content for Developers