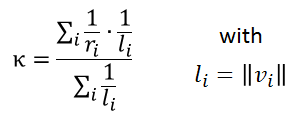Users:Structural Optimization/Response Functions/SurfaceCurvature
Contents |
General Description
Short Info
In the field of structural optimization it is often necessary to apply a constraining of surface curvature in order to maintain manufacturing constraints. To this purpose, Carat++ provides an estimation tool to approximate the mean curvature at a surface node.
Estimation of nodal curvature
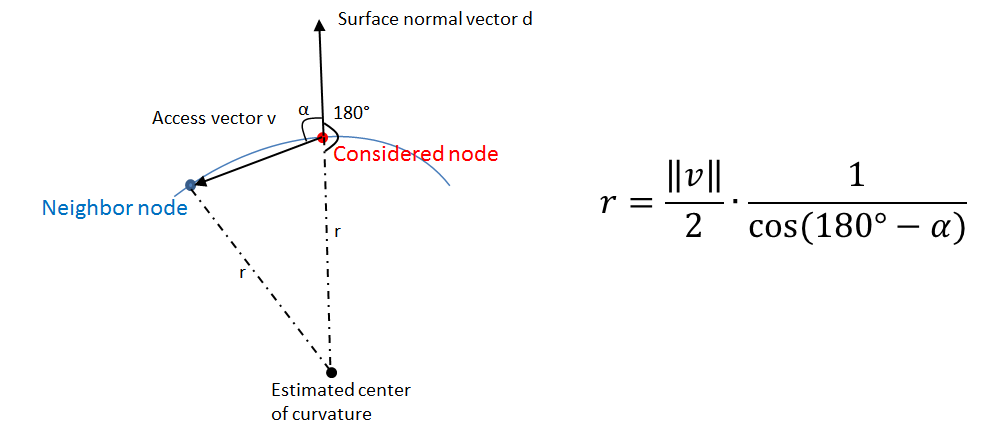
The nodal curvature is estimated using the surface normal vector and access vectors to the surrounding nodes. The estimation is based on a local spherical approximation of the geometry (see sketch below). So the radius of curvature r can be computed within the isosceles triangle.
Having computed this approximated radius of curvature for each surrounding node, the mean curvature of the surface is estimated by a weighted sum over all surrounding nodes i, whereat vi is the access vector to the ith node.
Kreisselmeier-Steinhauser weighting
Instead of constraining each single nodal curvature, Carat++ provides a technique to control the curvature within bigger element patches. To this purpose a Kreisselmeier-Steinhauser weighting is used.
Via the weighting parameter ρ the user can control to which extend exceedings of the maximum allowable curvature are weighted.
Input Parameters
| Block headline | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| OPT-RESPONSE_FCT | int : CURVATURE_PATCH_KS | Function ID and response function type. |
| Common compulsory parameters | ||
| ETA | real | Finite difference disturbance for sensitivity analysis |
| GRAD | DIRECT, ADJOINT | Method of gradient computation |
| SA | GLOBAL_FD, SEMI_ANALYTIC, EXACT_SEMI_ANALYTIC, ANALYTIC | Method of derivative computations inside sensitivity analysis |
| FDA | FOREWARD, CENTRAL, BACKWARD | Method of finite difference approximation (if neccessary for the chosen sensitivity analysis method) |
| DESVAR | OPT-VAR vector of integers | Design variables that are considered in the sensitivity analysis of this response function |
| Common optional parameters | ||
| WEIGHT | real, 1.0* | The weighting factor for this response function in multi-objective optimization |
| ANALYSIS | PC-ANALYSIS int | ID of the underlying analysis |
| Specific parameters | ||
| NODES | ND-SET int | Node set that includes all nodes this response function yields onto. |
| PATCH_SIZE | int | Size of patches (number of element rows) into which the NODES is sub-divided. |
| RHO | real | KS-weighting factor. |
| Common Compulsory Parameters for Constraints | ||
| Parameter | Values, Default(*) | Description |
| REL_LIMIT | real | Relative limit for constraint, depending on the actual value. |
| ABS_LIMIT | real | Absolute limit for constraint. Only one limit can be defined for a constraint. |
| CONSTRAINT_TYPE | INEQUALITY_LT, INEQUALITY_GT, EQUALITY | Type of constraint |
| Common Optional Parameters for Constraints | ||
| REL_TOLERANCE | real, 0* | Upper relative limit until which an inactive constraint is concidered as an active one |
| LAMBDA_ABS_MAX | real, 1/cepsilon* | Upper limit for lagrangian multiplier |
Example of a Complete Input Block
OPT-RESPONSE_FCT 1 : CURVATURE_PATCH_KS WEIGHT=1.0 ETA=1e-06 GRAD=ADJOINT SA= SEMI_ANALYTIC FDA=FOREWARD DESVAR=OPT-VAR 1 ! -- specific parameters NODES=ND-SET 1 PATCH_SIZE = 5 RHO = 15 ! -- constraint parameters ABS_LIMIT = 0.25 ! KAPPA_MAX REL_TOLERANCE = 0.1 CONSTRAINT_TYPE = INEQUALITY_LT LAMBDA_ABS_MAX = 40
A complete test example
Model description
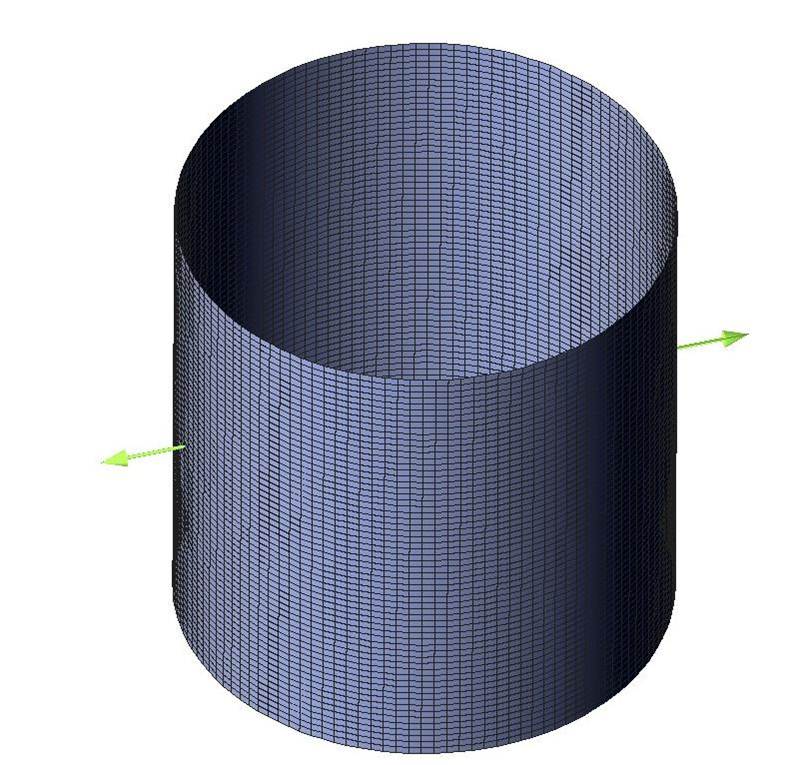
The considered test example is the optimization of a pinched cylinder applying a curvature limitation.
The curvature is controlled via a CURVATURE_PATCH_KS-function using a patch-size of 10 and a rho-parameter of 15. The kappa_max value is set to 7.0.
Input File
Here the full input file can be downloaded.
Documented Results
Based onto the user input, Carat++ automatically generated 22 patches and generated a constraint function for each of them. After 32 optimization steps all constraints are fulfilled and the maximum nodal curvature appearing is 8.4.
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |