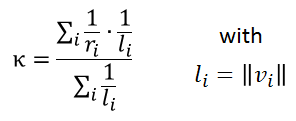Users:Structural Optimization/Response Functions/SurfaceCurvature
Contents |
General Description
Short Info
In the field of structural optimization it is often necessary to apply a constraining of surface curvature in order to maintain manufacturing constraints. To this purpose, Carat++ provides an estimation tool to approximate the mean curvature at a surface node.
Estimation of nodal curvature
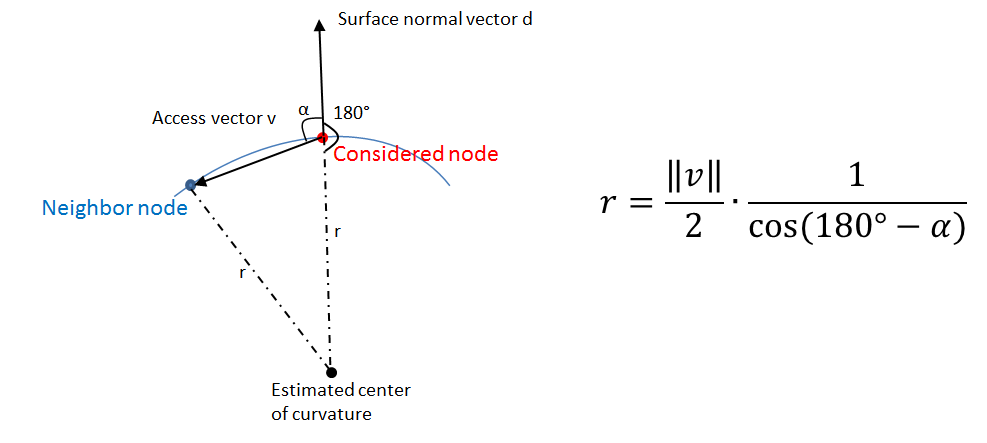
The nodal curvature is estimated using the surface normal vector and access vectors to the surrounding nodes. The estimation is based on a local spherical approximation of the geometry (see sketch below). So the radius of curvature r can be computed within the isosceles triangle.
Having computed this approximated radius of curvature for each surrounding node, the mean curvature of the surface is estimated by a weighted sum over all surrounding nodes i, whereat vi is the access vector to the ith node.
Kreisselmeier-Steinhauser weighting
Instead of constraining each single nodal curvature, Carat++ provides a technique to control the curvature within bigger element patches. To this purpose a Kreisselmeier-Steinhauser weighting is used.
Via the weighting parameter ρ the user can control to which extend exceedings of the maximum allowable curvature are weighted.
Input Parameters
| Block headline | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| OPT-RESPONSE_FCT | int : CURVATURE_PATCH_KS | Function ID and response function type. |
| Common compulsory parameters | ||
| ETA | real | Finite difference disturbance for sensitivity analysis |
| GRAD | DIRECT, ADJOINT | Method of gradient computation |
| SA | GLOBAL_FD, SEMI_ANALYTIC, EXACT_SEMI_ANALYTIC, ANALYTIC | Method of derivative computations inside sensitivity analysis |
| FDA | FOREWARD, CENTRAL, BACKWARD | Method of finite difference approximation (if neccessary for the chosen sensitivity analysis method) |
| DESVAR | OPT-VAR vector of integers | Design variables that are considered in the sensitivity analysis of this response function |
| Common optional parameters | ||
| WEIGHT | real, 1.0* | The weighting factor for this response function in multi-objective optimization |
| ANALYSIS | PC-ANALYSIS int | ID of the underlying analysis |
| Specific parameters | ||
| NUM_EIGENVALUE | int | Number of eigenvalue to be considered. NUM_VALUE has to be smaller or equal the NUM_ROOT flag inside the eigenvalue analysis. |
| Common Compulsory Parameters for Constraints | ||
| Parameter | Values, Default(*) | Description |
| REL_LIMIT | real | Relative limit for constraint, depending on the actual value. |
| ABS_LIMIT | real | Absolute limit for constraint. Only one limit can be defined for a constraint. |
| CONSTRAINT_TYPE | INEQUALITY_LT, INEQUALITY_GT, EQUALITY | Type of constraint |
| Common Optional Parameters for Constraints | ||
| REL_TOLERANCE | real, 0* | Upper relative limit until which an inactive constraint is concidered as an active one |
| LAMBDA_ABS_MAX | real, 1/cepsilon* | Upper limit for lagrangian multiplier |
Example of a Complete Input Block
OPT-RESPONSE_FCT 1 : EIGENVALUE WEIGHT=1.0 ANALYSIS=PC-ANALYSIS 1 ETA=1e-06 GRAD=ADJOINT SA=SEMI_ANALYTIC FDA=FOREWARD ! -- response function dependant parameters NUM_EIGENVALUE = 1 ! -- constraint parameters REL_LIMIT = 1.1 REL_TOLERANCE = 0.1 CONSTRAINT_TYPE = INEQUALITY_LT LAMBDA_ABS_MAX = 20
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |