Users:Structural Optimization/Response Functions/Strain Energy
Contents |
General Description
Short Info
Strain energy or compliance is a very popular objective function for structural optimization problems. Minimizing the strain energy of a structure yields to designs with optimal load carrying behavior and minimal displacements. At the same time the material strains and stresses are reduced.
Linear strain energy is commonly formulated by
- f = 1/2 dT Kel d
with the linear elastic stiffness matrix Kel and the displacement field d. The response function for linear strain energy requires the ID of a linear static analysis specified for parameter 'ANALYSIS'.
The formulation of nonlinear strain energy differs significantly from the linear formulation. It is defined by
- f = 1/2 fextT d
where fext describes the external forces. Whenever a model shows significant structural displacements, the optimization should the performed with respect to nonlinear strain energy. In this case the load carrying behavior of the deformed structure is optimized which usually ends up in more efficient designs. The response function for nonlinear strain energy requires the ID of a nonlinear static analysis specified for parameter 'ANALYSIS'.
Input Parameters
| Block headline | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| OPT-RESPONSE_FCT | int : STRAIN_ENERGY_LIN or STRAIN_ENERGY_NONLIN | Function ID and type mechanical problem. |
| Common compulsory parameters | ||
| ETA | real | Finite difference disturbance for sensitivity analysis |
| GRAD | DIRECT, ADJOINT | Method of gradient computation |
| SA | GLOBAL_FD, SEMI_ANALYTIC, EXACT_SEMI_ANALYTIC, ANALYTIC | Method of derivative computations inside sensitivity analysis |
| FDA | FOREWARD, CENTRAL, BACKWARD | Method of finite difference approximation (if neccessary for the chosen sensitivity analysis method) |
| DESVAR | OPT-VAR vector of integers | Design variables that are considered in the sensitivity analysis of this response function |
| Common optional parameters | ||
| WEIGHT | real, 1.0* | The weighting factor for this response function in multi-objective optimization |
| ANALYSIS | PC-ANALYSIS int | ID of the underlying analysis |
| Specific parameters | ||
| LOAD_CONSTANT | 0, 1 | Determines if an underlying non-linear analysis keeps the load constant during optimization (1) or not (0) |
| Common Compulsory Parameters for Constraints | ||
| Parameter | Values, Default(*) | Description |
| REL_LIMIT | real | Relative limit for constraint, depending on the actual value. |
| ABS_LIMIT | real | Absolute limit for constraint. Only one limit can be defined for a constraint. |
| CONSTRAINT_TYPE | INEQUALITY_LT, INEQUALITY_GT, EQUALITY | Type of constraint |
| Common Optional Parameters for Constraints | ||
| REL_TOLERANCE | real, 0* | Upper relative limit until which an inactive constraint is concidered as an active one |
| LAMBDA_ABS_MAX | real, 1/cepsilon* | Upper limit for lagrangian multiplier |
Example of a Complete Input Block
OPT-RESPONSE_FCT 1 : STRAIN_ENERGY_LIN ! -- basic stuff WEIGHT=1.0 ANALYSIS=PC-ANALYSIS 1 ETA=1e-06 GRAD=ADJOINT SA=SEMI_ANALYTIC FDA=FOREWARD DESVAR=OPT-VAR 1,2,3,4,5,6 ! -- constraint parameters ABS_LIMIT = 1-e3 REL_TOLERANCE = 0.1 CONSTRAINT_TYPE = INEQUALITY_LT LAMBDA_ABS_MAX = 20
Examples
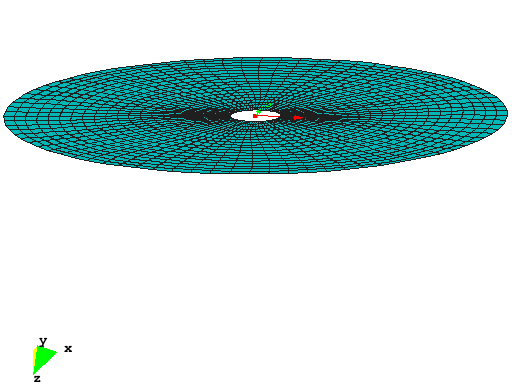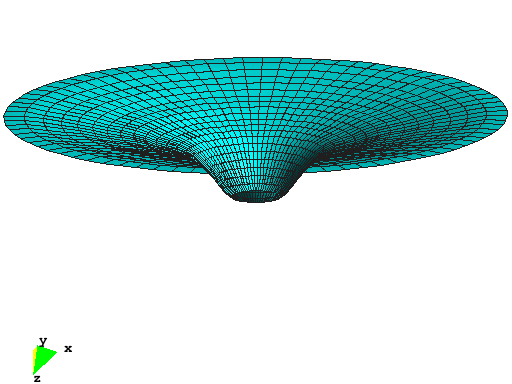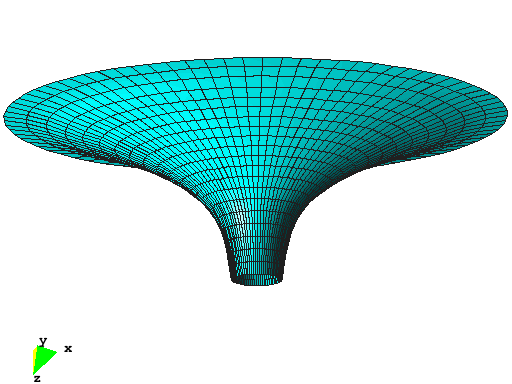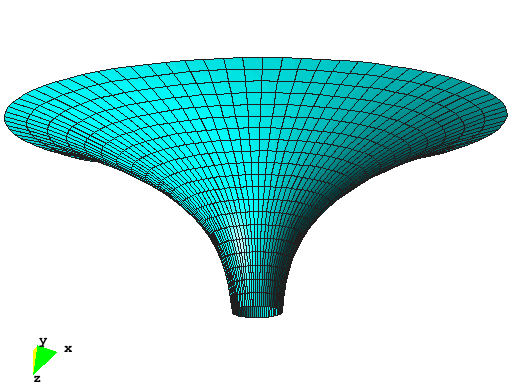
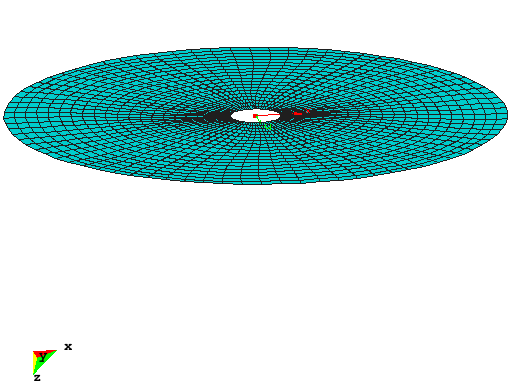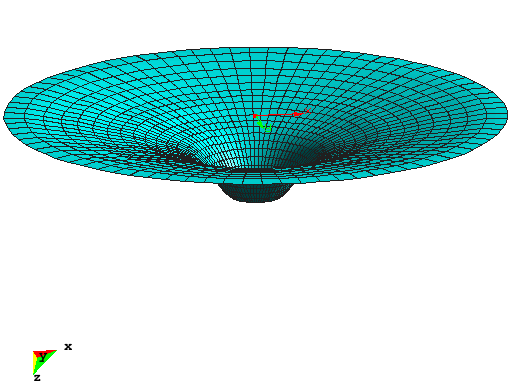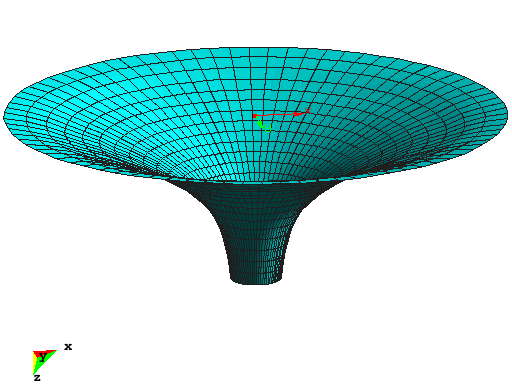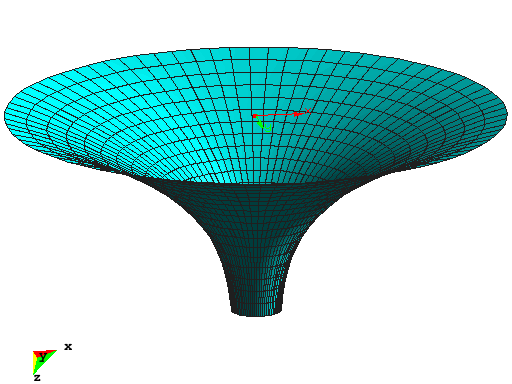
Cup Structure
This example shows the optimal shape of a cup structure with respect to linear strain energy. The structure was motivated by natural shapes of some types of mushrooms or the calyx of flowers. The inner ring of the structure is supported and the cup is subjected to dead load. The initial design is completely flat, whereas the optimal structure has a specified height of 8m. The material is described by the St.Venant-Kirchhoff material model with standard concrete properties. The overall dimensions of the optimized structure are:
- Height = 8m
- Radius of inner ring = 1m
- Radius of outer ring = 10m
- Thickness (const.) = 0.05m
The optimization problem is solved by the Augmented Lagrangian Multiplier method where the structural height of 8m is implemented as equality constraint.
Bottom view to Design Development
Top view to Design Development
Bead optimization
Another important application of strain energy minimization is bead optimization of metal sheets. Beads can be considered as local stiffeners that improve the load carrying behavior. The optimal orientation, length, and width of the beads is a challenging job for numerical optimization schemes. The figure below shows an optimized metal sheet with corner support and central loading. The bead height is restricted by proper variable bounds. It can be easily observed that the optimized structure has much better mechanical properties (smaller displacements, smaller stresses) than the flat blank.
Rendered view of optimal bead geometry
Colored view to optimal bead geometry
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |
