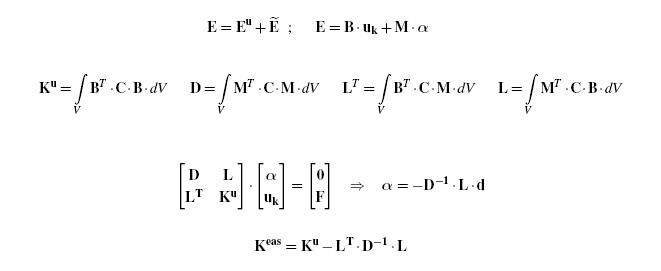Users:General FEM Analysis/Elements Reference/SolidHexa1

Contents 1 General Description 1.1 Element Type 1.2 Degrees of Freedom 2 Input Parameters 2.1 Parameter Description 2.2 Example of a Complete Input Block 3 Element Loading 3.1 Dead Load 3.2 Temperature Load 4 The EAS Method 5 References

General Description

Element Type

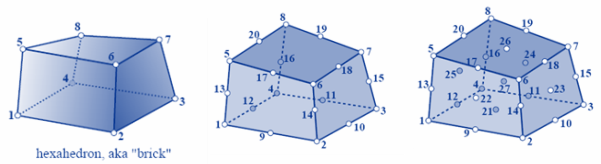
• This element class provides 3D hexahedral elements with linear (8-noded element), partially quadratic (20-noded) or quadratic shape functions (27-noded)
• The element formulation includes an enhanmced assumed strain (EAS) improvement in order to avoid locking effects. This feature is only available for 8-noded elements and usage is only recommended in geometrically linear computations.

Degrees of Freedom

All hexahedral elements use three translatoric degrees of freedom at each node.
They are named Disp_X, Disp_Y, Disp_Z.

Input Parameters

Parameter Description

Compulsory Parameters
Parameter	Values, Default(*)	Description
MAT	EL-MAT int	Linking to a material input block
INT_TYPE_HEXA	FULL, REDUCED	Control of integration type 20-noded elements are able to perform a uniform reduced integration (2x2x2 instead of 3x3x3) without hourglassing stabilisation
Optional Parameters
Parameter	Values, Default(*)	Description
EAS	int	Flag Enhances Assumed Strains (EAS) method Possible values are: 0* = EAS off 9 = full and locking free linear strains can be described (recommended for one axial bending) 15 = ellimination of parasitic bi-linear strains 24 = full and locking free bi-linear strains can be described (recommended for two axial bending) 30 = full tri-linear strains can be described

Example of a Complete Input Block

EL-PROP 1: SOLIDHEXA1
MAT           = EL-MAT 1
INT_TYPE_HEXA = FULL
EAS           = 0

Inside the property block there is no distinction between linear and quadratic formulated elements. It is possible to define 8-noded, 20-noded and 27-noded elements using one and the same element property (assuming that no EAS is used):

 !  ElementID  Part-ID       EL-PROP             Node-IDs
NEL  1           1             1            1  2  3  4  5  6  7  8                                                                  ! 8-noded element
NEL  2           1             1            20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 36 38 39 40                          !20-noded element
NEL  3           1             1            50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 66 68 69 70 71 72 73 74 75 76 77     !27-noded element

Element Loading

Hexahedral elements are able to carry two types of element loads:

• dead load
• temperature load

Dead Load

Dead weight of an element is computed by multiplying material's denisity (ρ) with gravity's acceleration, which has to be defined inside the load block concearning its direction and size.
An example for a load definition of a concrete structure (assuming linear elastic isotropic material behaviour) with gravity acting in positive z-direction would look like

EL-MAT 1 : LIN_ELAST_ISOTROPIC
EMOD=3.5e10  ALPHAT=1e-5  DENS=2.5e3  NUE=0.2

LD-ELEM 1 PART=1 
 TYPE=DEAD      D1=0.0   D2=0.0   D3=1.0  VAL=9.81

whereat the finite elemet model is based on SI units (m, N, kg).

Temperature Load

This paragraph only focuses at element specific topics concearing temperature load. For more detailed descriptions please look at the load documentation

For the computation of temperature loads solid elements do not concider any layer of laminate structure within the element. So only the temperature defined for layer number one is considered at each node.
The combination of temperature loading and EAS improvement is possible.

LD-ELEM 1  
 sTYPE = TEMPERATURE
 ND-SET = 1  LAYER = 1  VAL = +10
 ND-SET = 2  LAYER = 1  VAL = -10

The EAS Method

The idea of enhanced assumed strains is to enlarge the element srain field by a set of additional strains in order to enable the element to express certain states of displacement without locking due to parasitic strains. ^{[1] [2]}.

To this purpose the strain-displacement relation is enlarged by additional terms which leads to a modified element stiffness matrix:

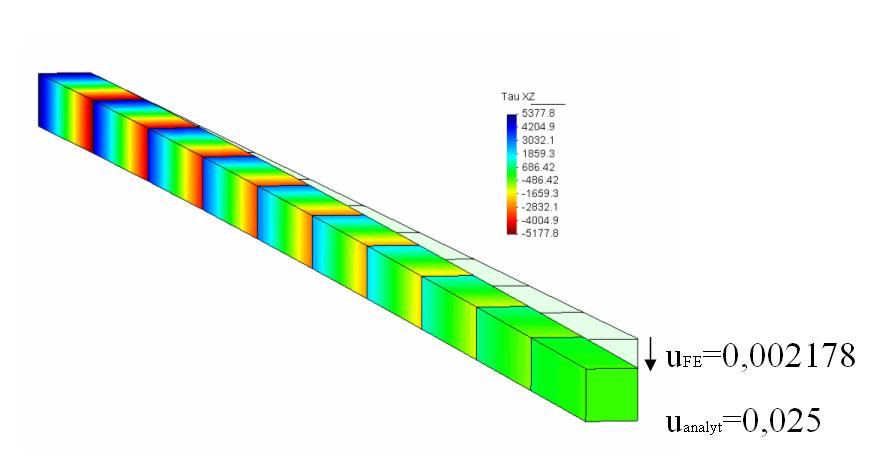
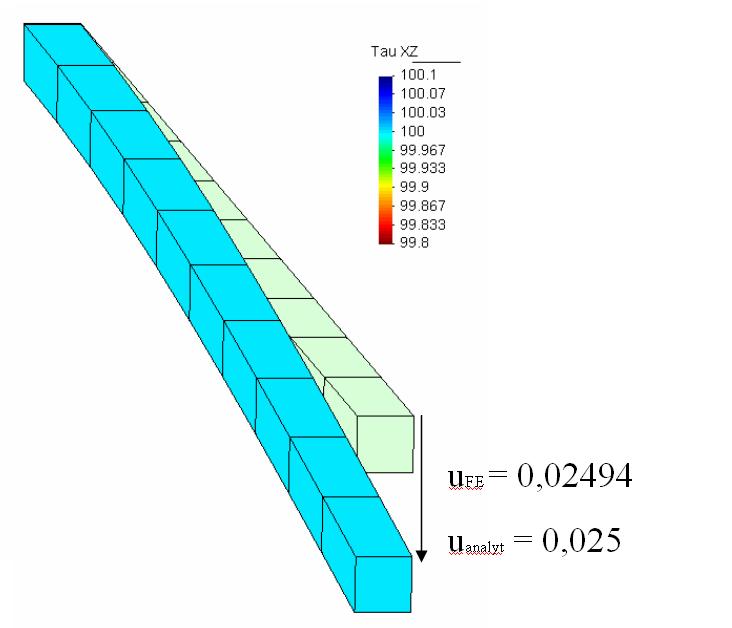
The following example will show the benefit of EAS improved elements toward purely displacment formulated eight-noded hexahedrals. The investigated system is a tip loaded cantilever wherby the cross section is modeled by one element.

Element HEXA8	Element HEXA8EAS9

The pure displacement based elements show the well known in-plane shear locking which increases along the cantilever with increasing bending moment. As artificial strain/shear produces artificial stiffness, the tip displacement is extremly under estimated.

In contrast the EAS improved elements are able to eliminate artificial strains arrising from locking, and so tip displacement is described correctly.

References

1. ↑ J.C. Simo, M.S. Rifai: „A class of mixed assumed strain methods and the method of incompatible modes“, in „International Journal for Numerical Methods in Enginee- ering“, Vol. 29, 1990, pages 1595-1638
2. ↑ U. Andelfinger, E. Ramm: „EAS-Elements for two-dimensional, three-dimensional, plate and shell structures and their equivalence to HR-Elements“, in „International Journal for Numerical Methods in Engineeering“, Vol. 36, 1993, pages 1311-1337

Whos here now:   Members 0   Guests 0   Bots & Crawlers 1