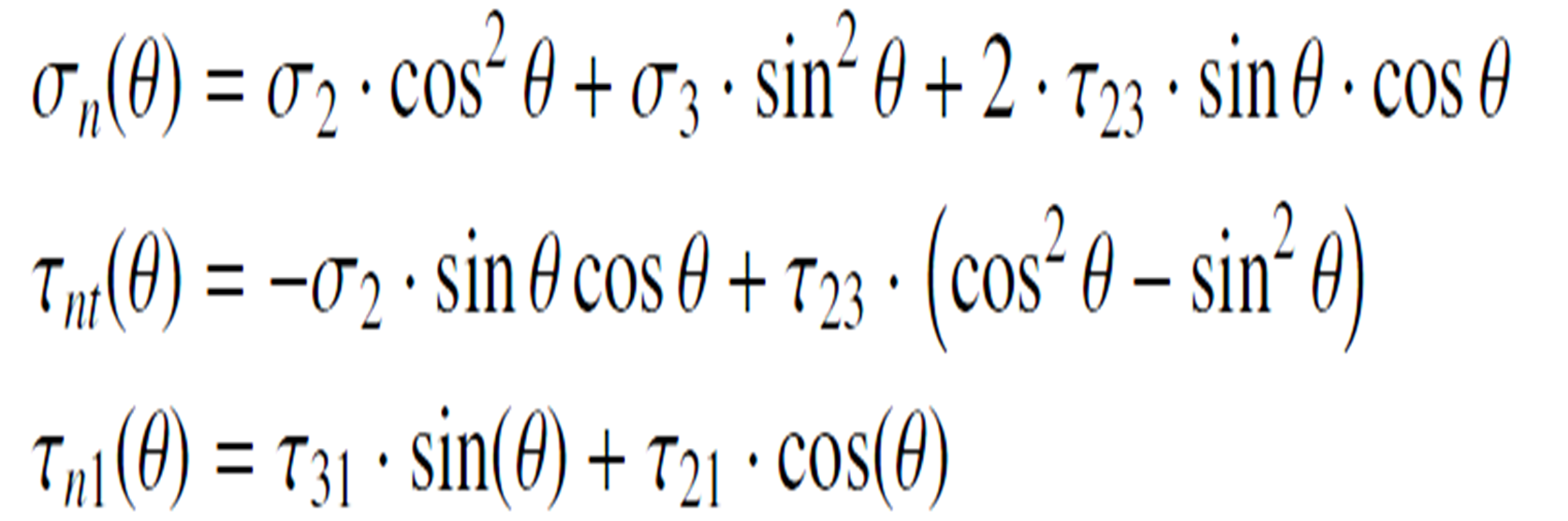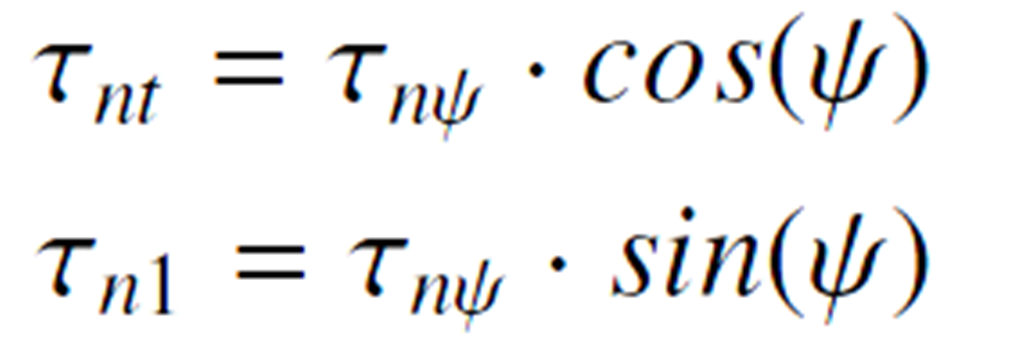Users:General FEM Analysis/Materials Reference/Puck Failure Criterion
From Carat++ Public Wiki
(Difference between revisions)
| Line 27: | Line 27: | ||
In order to judge if a stress vector on the stress spce is leading to damage, a mathematical expression is needed. | In order to judge if a stress vector on the stress spce is leading to damage, a mathematical expression is needed. | ||
This expression is called ''fracture condition'' an is written as the following general form: | This expression is called ''fracture condition'' an is written as the following general form: | ||
| + | |||
| + | |||
[[File:Formel3.4.png|150px]] | [[File:Formel3.4.png|150px]] | ||
| − | [[File:sigma_i.png| | + | |
| + | |||
| + | [[File:sigma_i.png|15px]] : Components of stress vector | ||
| + | |||
Ri : Strengths under corresponding stresses | Ri : Strengths under corresponding stresses | ||
| + | |||
F : Fracture function | F : Fracture function | ||
| + | |||
[[File:puck.png|1000px]] | [[File:puck.png|1000px]] | ||
Revision as of 07:31, 15 February 2013
Contents |
General Description
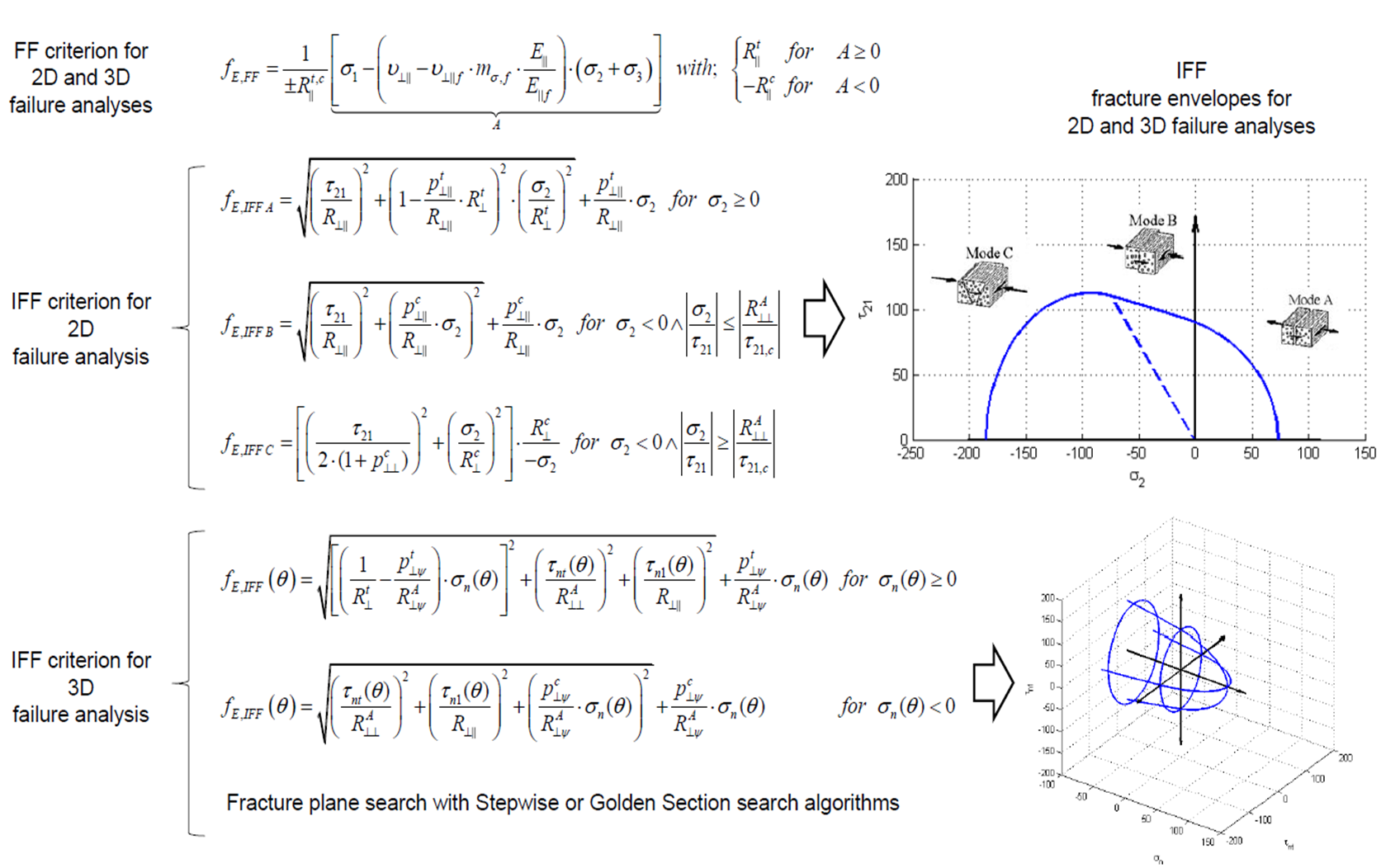
It is based on Mohr‘s fracture hypothesis which is appropriate for brittle fracture behaviour of composite materials. It can distinguish between fibre fracture and different inter-fibre fracture. Both 2D and 3D formulations are implemented into Carat++. Available fracture modes for 2D Puck Criterion are:
- Fibre Fracture (FF)
- Inter Fibre Fracture Mode A (IFF A)
- Inter Fibre Fracture Mode B (IFF B)
- Inter Fibre Fracture Mode C (IFF C)
Available fracture modes for 3D Puck Criterion are:
- Fibre Fracture (FF)
- Inter Fibre Fracture (IFF)
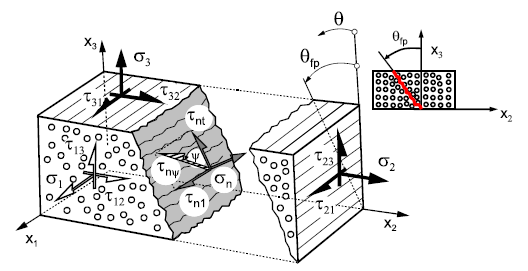
Stresses on the Fracture Plane
Strength Analysis
In order to judge if a stress vector on the stress spce is leading to damage, a mathematical expression is needed. This expression is called fracture condition an is written as the following general form:
: Components of stress vector
Ri : Strengths under corresponding stresses
F : Fracture function
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| EF | real | Elasticity modulus of the fibres |
| RTL | real | Resistance to longitudinal tension (Direction 1) |
| RCL | real | Resistance to longitudinal compression (Direction 1) |
| RTT | real | Resistance to transverse tension (Direction 2) |
| RCT | real | Resistance to transverse compression (Direction 2) |
| RSL | real | Resistance to longitudinal shear |
| VFF | real | Volume fraction of the fibres |
| PTTL | real | Inclination parameter,
|
| PCTL | real | Inclination parameter,
|
| Optional Parameters | ||
| Parameter | Values, Default(*) | Description |
| STRESS TYPE | 2D, 3D | Indicates what kind of stress state should be used to calculate the failure condition. When not given, related element’s stress type is taken. |
| NUE12F | real | Poisson’s ratio for fibres. (De f ault = 0.2) |
| MGF | real | Amplification factor (De f ault = 1.2) |
| S, M | real | Parameters necessary for calculation of weakening due to  (De f ault = S = M = 0.5)
|
| PTT | real | Inclination parameter  . When not given, calculated using the strength values. See Section 3.1.2.3
|
| WEAKENING | int | Switch for calculation of weakening due to .
|
| FPS | SWS*, GSS | Switch for fracture plane search algorithm.
|
| FPS_SWS_SIZE | real | Step size for step-wise fracture plane search |
Example of a Complete Input Block
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |
