Users:General FEM Analysis/Elements Reference/Shell10
(Created page with 'Category: Users:General FEM == General Description == {| |Triangular Shell8 elements |[[File:Element_shell8_quadrilatera…') |
|||
| Line 4: | Line 4: | ||
{| | {| | ||
| − | |[[File: | + | |[[File:Element_shell10_triangle_topo.jpg|frame|up|Triangular Shell10 element]] |
| − | |[[File: | + | |[[File:Element_shell10_quadrilateral_topo.jpg|frame|up|Quadrilateral Shell10 element]] |
|} | |} | ||
| Line 12: | Line 12: | ||
=== Element Type === | === Element Type === | ||
| − | * This shell element is a | + | * This shell element is a rotationfree shell element with 3 (external) degrees of freedom per node. |
| − | * It | + | * It has Kirchhoff-Love kinematics. |
| − | * | + | * Underlying element is the Membrane1 element and additional bending stiffness is added for each dof. |
| − | * | + | * Curvature information is calculated out of neighboring elements. |
| − | [[File: | + | [[File:Patch_example-eps-converted-to.pdf|border|up|Example Patch]] |
| − | + | ||
=== Degrees of Freedom === | === Degrees of Freedom === | ||
| Line 24: | Line 23: | ||
The degrees of freedom are: | The degrees of freedom are: | ||
* the 3 translatoric components of the shell midplaine in the global cartesian frame (the 3 "classical" translatoric DOFs): They are named ''Disp_X'', ''Disp_Y'', ''Disp_Z''. | * the 3 translatoric components of the shell midplaine in the global cartesian frame (the 3 "classical" translatoric DOFs): They are named ''Disp_X'', ''Disp_Y'', ''Disp_Z''. | ||
| − | |||
| − | |||
| − | |||
== Input Parameters == | == Input Parameters == | ||
| + | |||
| + | === Parameter Description === | ||
=== Parameter Description === | === Parameter Description === | ||
| Line 42: | Line 40: | ||
!MAT | !MAT | ||
|EL-MAT ''int'' | |EL-MAT ''int'' | ||
| − | | | + | |Number for the used Material |
| + | e.g. MAT=EL-MAT 1 | ||
|- | |- | ||
| − | ! | + | !THICKNESS |
| − | | | + | |''int'' |
| − | | | + | |Thickness of the shell |
|- | |- | ||
| − | ! | + | !A_X, A_Y, A_Z |
| − | + | B_X, B_Y, B_Z | |
| − | | | + | | |
| − | + | |Definition of the principle directions of the surface. To define the prestress dirctions. (see Membrane1 element) | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | ! | + | !SIG11 |
| − | | | + | SIG22 |
| − | | | + | SIG12 |
| − | + | | | |
| − | + | |Prestress state of the membrane. (see Membrane1 element) | |
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | ! | + | !CURV_TYPE_SHELL10 |
| − | + | |''CEG, CIN'' | |
| − | + | |Definition of curvature calculation type. CIN for curvature through interpolated normal field. CEG for curvature through enhanced geometry. (see description below) | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |'' | + | |
| − | | | + | |
|- | |- | ||
|colspan="3" style="background:#efefef;"| Optional Parameters | |colspan="3" style="background:#efefef;"| Optional Parameters | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| Line 89: | Line 68: | ||
=== Example of a Complete Input Block === | === Example of a Complete Input Block === | ||
<pre> | <pre> | ||
| − | EL-PROP 1 : | + | EL-PROP 1 : SHELL10 |
MAT=EL-MAT 1 | MAT=EL-MAT 1 | ||
THICKNESS=0.1 | THICKNESS=0.1 | ||
| − | + | INT_TYPE_SHELL10 = FULL | |
| − | + | CURV_TYPE_SHELL10 = CEG | |
| − | + | PRESTRESS SIG11=0.0 SIG22=0.0 SIG12=0.0 | |
| − | + | A_X=1.0 A_Y=0.0 A_Z=0.0 | |
| − | + | B_X=0.0 B_Y=1.0 B_Z=0.0 | |
</pre> | </pre> | ||
| Line 110: | Line 89: | ||
== Theory == | == Theory == | ||
| − | The theory and finite element formulation is originally based on the work of | + | The theory and finite element formulation is originally based on the work of Linhard |
| − | <ref name= | + | <ref name=Lin2007">Linhard, J.; Wüchner, R.; Bletzinger K.U.: "Upgrading" membranes to shells — The CEG rotation free shell |
| − | + | element and its application in structural analysis, Finite Elements in Analysis and Design, Elsevier, volume 44, pages 63-74, 2007</ref> | |
| − | + | ||
| − | + | For the correct use of the Shell10 and the interpretation of related results, the following aspects should be considered: | |
| − | + | ||
| − | + | === Decomposition of virtual work === | |
| − | + | ||
| + | For the derivation the principle of virtual work [[File:Formula_pvd.png|175px]] is splitted into membrane and bending parts: [[File:Formula_splitup.png|200px]] | ||
| + | The bending part is calculated with [[File:Formula_bendingpart.png|175px]] consisting out of moments acting on changes of curvature. With an ideal linear elastic material law, e.g. St. Venant-Kirchhoff model, these moments can be related to the change of curvature with: [[File:Formula_stvenantkirchhoff.png|300px]]. Finally the change of curvature can be calculated with: [[File:Formula_change_of_curvature.png|300px]]. The interesting part is how curvature related quantites on C0-continious meshes. | ||
| + | |||
| + | === Curvature on C0 continous finite element meshes === | ||
| + | |||
| + | While isoparametric triangular elements are flat, quadrilateral elements allready bring a curvature along, but which is not sufficient for the calculation of a surface curvature. | ||
| + | |||
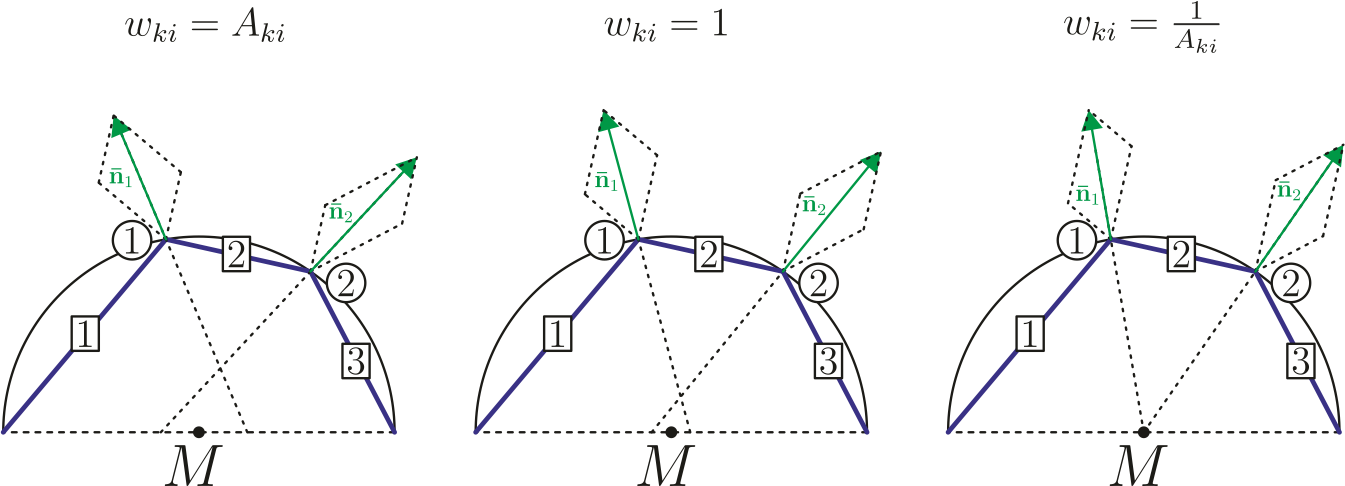
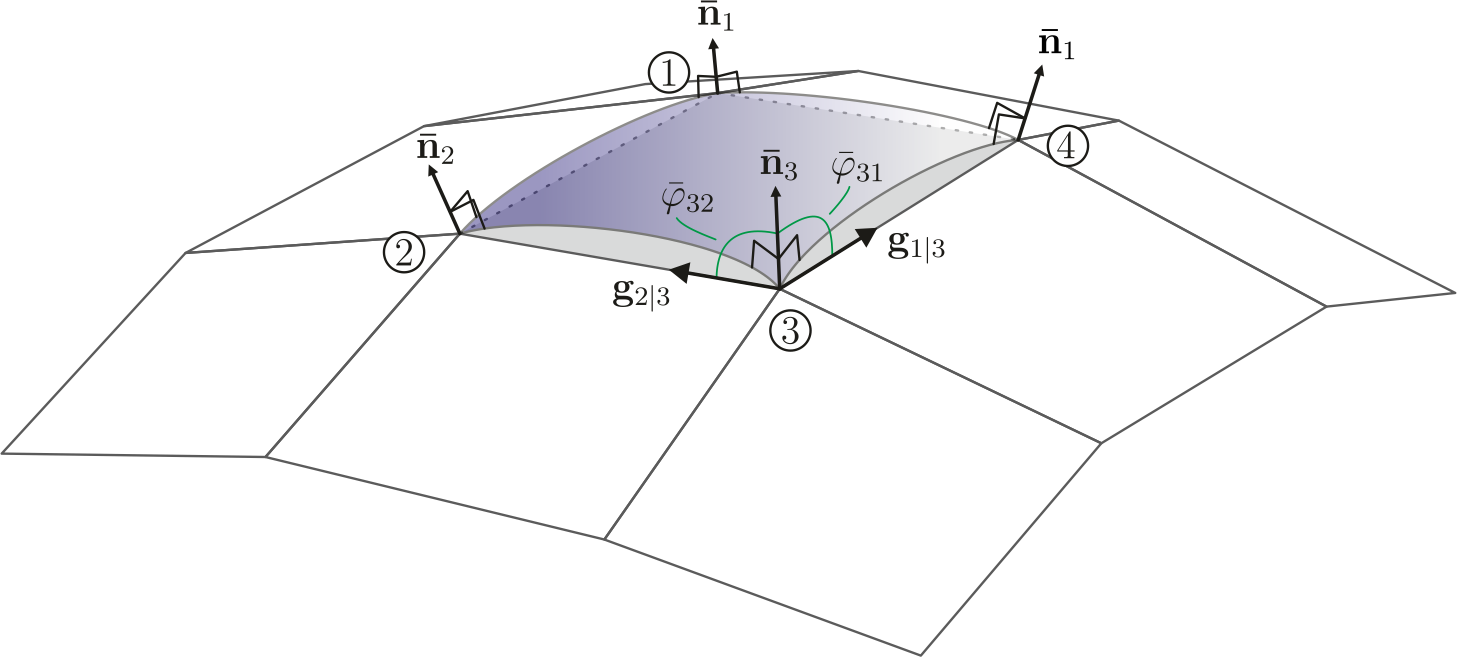
| + | The basic idea is to extend the normal vector at the nodes with information of the neighbouring elements. The so called "nodal director" is the averaged normalized normal vector at each node and calulated with: [[File:Formula.png|175px]]. The weighting factors are the approximated area of the corresponding element. It can be shown that for a two dimensional discretized half-circle these weighting factors exactly reproduce the surface normals. | ||
| + | |||
| + | [[File:Weighting_factor.png|600px|up|Different weighting factors]] | ||
| + | |||
| + | ==== CIN: curvature through interpolated normal vectors ==== | ||
| + | |||
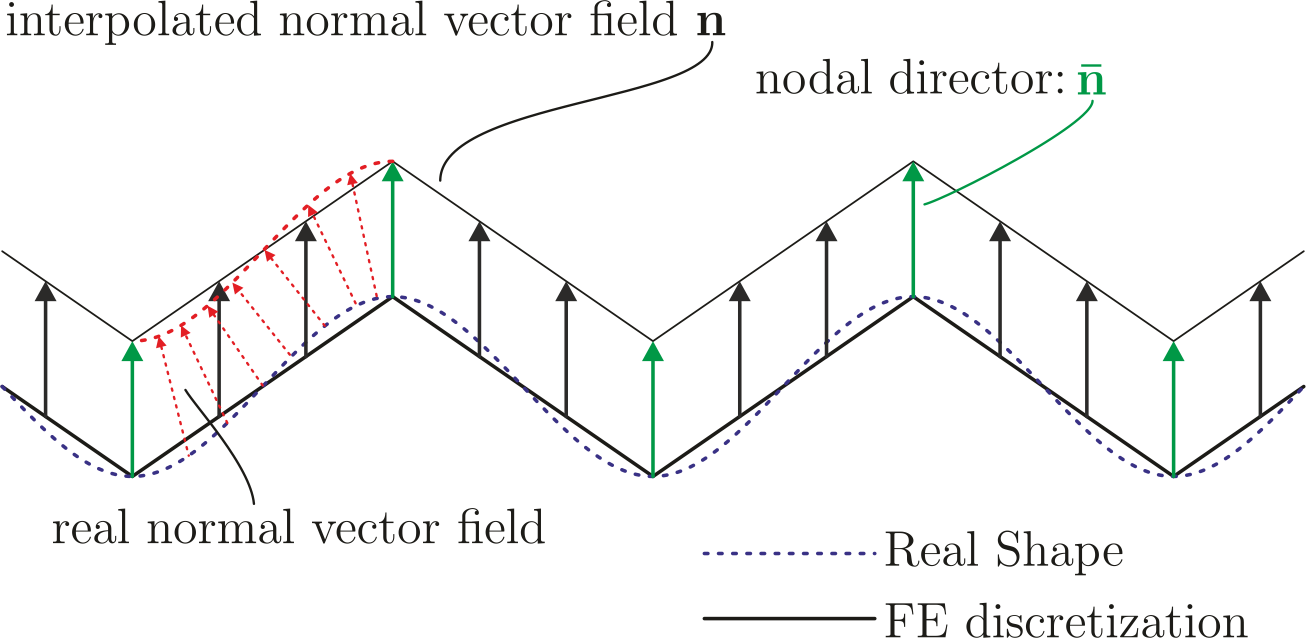
| + | For the curvature calculation the straightforward approach is to use the curvature tensor introduced in classical differential geometry on the discretized geometry. Since the normal vector is needed throughout the whole element the nodal director is interpolated with the same shape functions used for the isoparametric element. This formulation results in a deficiency shown in the following figure. | ||
| + | |||
| + | [[File:Deficiency.png|600px|up|Deficiency of CIN operator]] | ||
| + | |||
| + | Due to the linear interpolation of the nodal directors, no change in the normal field will occur, hence no change of the curvature | ||
| + | can be detected. This represents a deformation, which can not be captured by the formulas and therefore will not enter the bending part of the internal virtual work. One therefore speaks of a zero-energy deformation mode. Performing analysis with this operator will in some cases produce this "zig-zag"-like results and the use of this curvature operator is not recommended. Examples of these unphysical deformation figures are shown below. | ||
| + | |||
| + | |||
| + | |||
| + | ==== CEG: curvature calculation through enhanced geometry ==== | ||
| + | |||
| + | In order to overcome these spurious deformation modes a second approach is implemented. The basic idea of this method of curvature calculation is to enhance the geometry with an additional rotation field. The nodal director of the surface is in general inclined | ||
| + | against the tangential plane of the specific isoparametric element, although it should be normal to it. In order to repair this discrepancy, additional rotations are introduced, which can be determined by the inclination of the nodal director against the tangential plane. These rotations are then interpolated using suitable shape functions. The enhanced curvature of a CEG element consists of the actual curvature of the isoparametric surface and the additional curvature obtained by the derivation of the introduced additional rotation field w.r.t the surface coordinates. | ||
| + | |||
| + | [[File:Discrete_rotations.png|600px|up|Discrete rotations on node 3 of a quadrilateral element]] | ||
| + | |||
| + | |||
=== Degrees of Freedom, Rotational DOFs, Moment Loads === | === Degrees of Freedom, Rotational DOFs, Moment Loads === | ||
| − | The degrees of freedom consist of the three displacements of the midsurface (according to standard shell theory) | + | The degrees of freedom consist of the three displacements of the midsurface (according to standard shell theory). This has to be taken into account at the formulation of BCs and Loads, especially at clamped supports. |
| − | + | ||
| − | + | ||
| − | + | ||
Revision as of 11:50, 23 January 2011
Contents
|
General Description
Element Type
- This shell element is a rotationfree shell element with 3 (external) degrees of freedom per node.
- It has Kirchhoff-Love kinematics.
- Underlying element is the Membrane1 element and additional bending stiffness is added for each dof.
- Curvature information is calculated out of neighboring elements.
File:Patch example-eps-converted-to.pdf
Degrees of Freedom
The degrees of freedom are:
- the 3 translatoric components of the shell midplaine in the global cartesian frame (the 3 "classical" translatoric DOFs): They are named Disp_X, Disp_Y, Disp_Z.
Input Parameters
Parameter Description
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| MAT | EL-MAT int | Number for the used Material
e.g. MAT=EL-MAT 1 |
| THICKNESS | int | Thickness of the shell |
| A_X, A_Y, A_Z
B_X, B_Y, B_Z |
Definition of the principle directions of the surface. To define the prestress dirctions. (see Membrane1 element) | |
| SIG11
SIG22 SIG12 |
Prestress state of the membrane. (see Membrane1 element) | |
| CURV_TYPE_SHELL10 | CEG, CIN | Definition of curvature calculation type. CIN for curvature through interpolated normal field. CEG for curvature through enhanced geometry. (see description below) |
| Optional Parameters | ||
Example of a Complete Input Block
EL-PROP 1 : SHELL10 MAT=EL-MAT 1 THICKNESS=0.1 INT_TYPE_SHELL10 = FULL CURV_TYPE_SHELL10 = CEG PRESTRESS SIG11=0.0 SIG22=0.0 SIG12=0.0 A_X=1.0 A_Y=0.0 A_Z=0.0 B_X=0.0 B_Y=1.0 B_Z=0.0
Element Loading
Pressure
Dead Load
Snow Load
Theory
The theory and finite element formulation is originally based on the work of Linhard [1]
For the correct use of the Shell10 and the interpretation of related results, the following aspects should be considered:
Decomposition of virtual work
For the derivation the principle of virtual work ![]() is splitted into membrane and bending parts:
is splitted into membrane and bending parts: ![]() The bending part is calculated with
The bending part is calculated with ![]() consisting out of moments acting on changes of curvature. With an ideal linear elastic material law, e.g. St. Venant-Kirchhoff model, these moments can be related to the change of curvature with:
consisting out of moments acting on changes of curvature. With an ideal linear elastic material law, e.g. St. Venant-Kirchhoff model, these moments can be related to the change of curvature with: 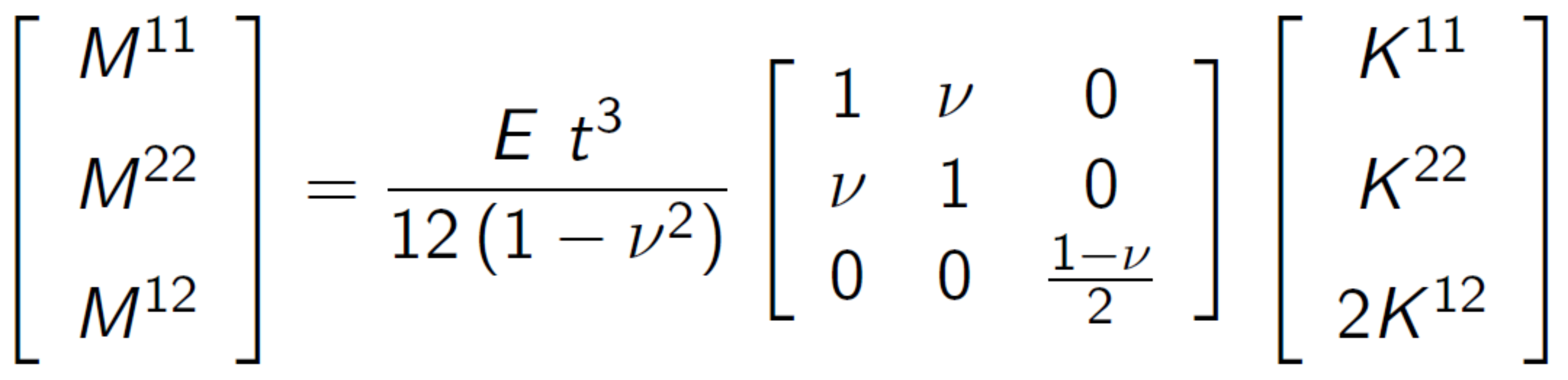 . Finally the change of curvature can be calculated with:
. Finally the change of curvature can be calculated with: ![]() . The interesting part is how curvature related quantites on C0-continious meshes.
. The interesting part is how curvature related quantites on C0-continious meshes.
Curvature on C0 continous finite element meshes
While isoparametric triangular elements are flat, quadrilateral elements allready bring a curvature along, but which is not sufficient for the calculation of a surface curvature.
The basic idea is to extend the normal vector at the nodes with information of the neighbouring elements. The so called "nodal director" is the averaged normalized normal vector at each node and calulated with: 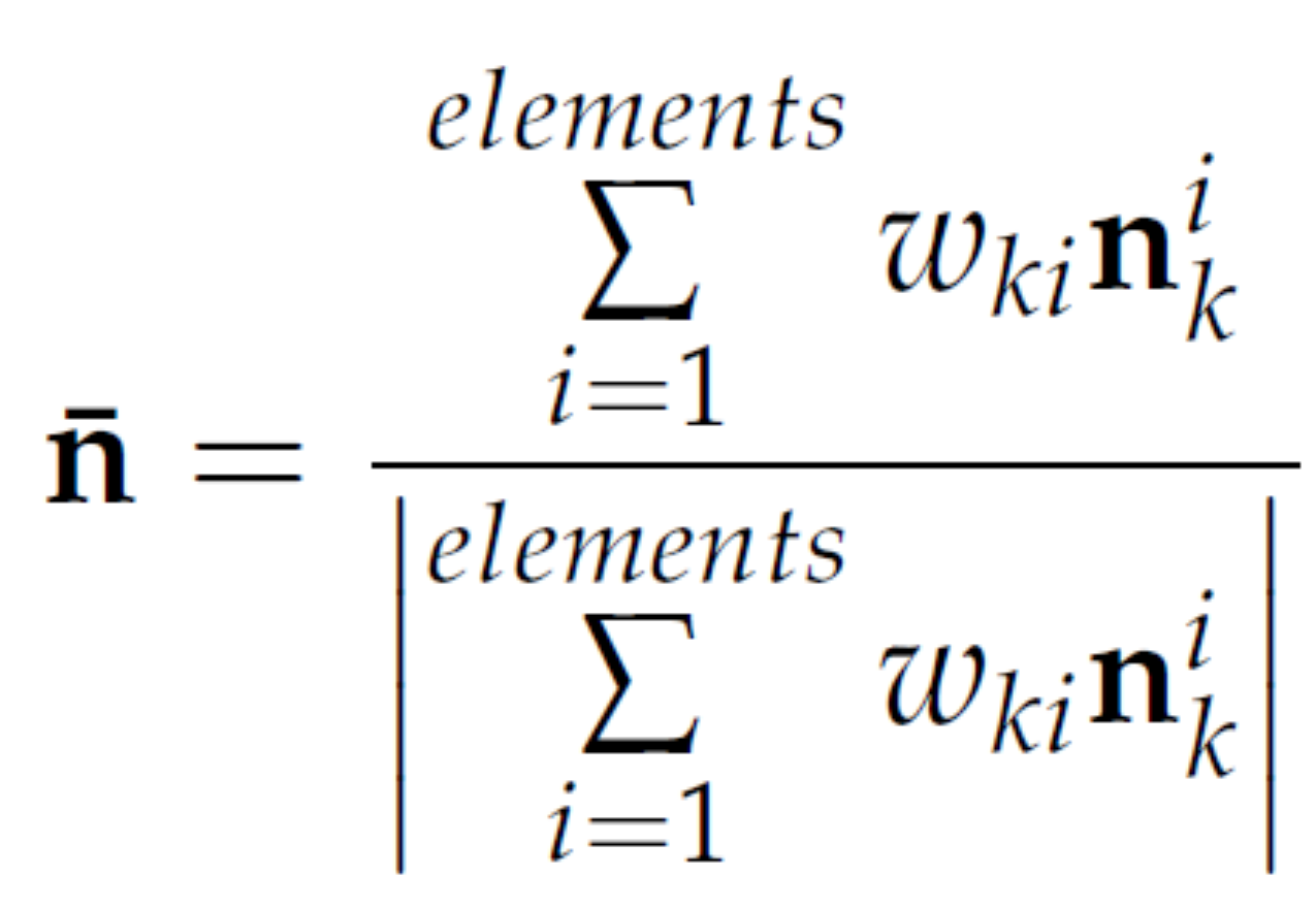 . The weighting factors are the approximated area of the corresponding element. It can be shown that for a two dimensional discretized half-circle these weighting factors exactly reproduce the surface normals.
. The weighting factors are the approximated area of the corresponding element. It can be shown that for a two dimensional discretized half-circle these weighting factors exactly reproduce the surface normals.
CIN: curvature through interpolated normal vectors
For the curvature calculation the straightforward approach is to use the curvature tensor introduced in classical differential geometry on the discretized geometry. Since the normal vector is needed throughout the whole element the nodal director is interpolated with the same shape functions used for the isoparametric element. This formulation results in a deficiency shown in the following figure.
Due to the linear interpolation of the nodal directors, no change in the normal field will occur, hence no change of the curvature can be detected. This represents a deformation, which can not be captured by the formulas and therefore will not enter the bending part of the internal virtual work. One therefore speaks of a zero-energy deformation mode. Performing analysis with this operator will in some cases produce this "zig-zag"-like results and the use of this curvature operator is not recommended. Examples of these unphysical deformation figures are shown below.
CEG: curvature calculation through enhanced geometry
In order to overcome these spurious deformation modes a second approach is implemented. The basic idea of this method of curvature calculation is to enhance the geometry with an additional rotation field. The nodal director of the surface is in general inclined against the tangential plane of the specific isoparametric element, although it should be normal to it. In order to repair this discrepancy, additional rotations are introduced, which can be determined by the inclination of the nodal director against the tangential plane. These rotations are then interpolated using suitable shape functions. The enhanced curvature of a CEG element consists of the actual curvature of the isoparametric surface and the additional curvature obtained by the derivation of the introduced additional rotation field w.r.t the surface coordinates.
Degrees of Freedom, Rotational DOFs, Moment Loads
The degrees of freedom consist of the three displacements of the midsurface (according to standard shell theory). This has to be taken into account at the formulation of BCs and Loads, especially at clamped supports.
Deformation in Thickness Direction
The three components of the deformation of the director also comprise a possible deformation in thickness direction (change of thickness). The three DOFs Dir_Diff_Shell8_X, Dir_Diff_Shell8_Y and Dir_Diff_Shell8_Z could be converted in two rotations and one deformation in thickness direction. However, the thickness deformation does not necessarily coincide with the 6th degree of freedom (Dir_Diff_Shell8_Z)! This would only be true, if the shell midplaine would be parallel to the xy-plane. In general, the thickness deformation is that component of the difference vector, which is parallel to the director (i.e. a linear combination of all three cartesian components).
In case of a fixed support, also the thickness deformation is fixed. This is correct in the context of real physical clamped supports, but it is wrong in the context of clamped supports that model symmetry conditions.
EAS Enhancement, 7-parameter formulation
In case of a nonzero Poisson ratio, the 6 nodal DOFs are not sufficient in order to describe a shell theory which is assymptotically correct for bending situations. That's why a seventh parameter is introduced via the EAS method. The interpolation of this parameter within the element is described by value 3 of the parameter EAS of the property block. It has to be at least constant, i.e. the value must be at least =1. In general, for quadrilateral element a bilinear interpolation is recommended ( i.e. EAS = x,x,4,x,x), for triangular elements a constant or linear interpolation is suggested (see table above).
Element Technology
The are different kind of locking effects for shells. An overview is given at [2].
- (Bi-)linear elements (3 noded, 4-noded) are almost completely free of membrane locking, thus EAS is not really necessary here. For this reason, these elements are in the context of shells superior to elements of higher order. EAS does not completely eliminate membrane locking, but pushes it back to values of a higher critical parameter (higher slenderness)
- transverse shear locking must always be tackled, either by EAS or by ANS. Only in the context of extremely thick structures, this can be turned down
- Also thickness locking must always be tackled, either by EAS or by ANS.
- The in-plane bending behaviour of (bi-)linear elements is very bad. If such kind of deformations are expected to show up, then the use of EAS is recommended for the 4-noded element. However, this locking behaviour cannot be eliminated for the 3-noded triangular element. However, the related locking phenomena (in-plane shear locking, volumetric locking) are usually less critical for shells compared to the aforementioned ones.
Mesh Generation
As the DOF formulation is based on the difference vector, the physical meaning of the fourth up to sixth degree of freedom is dependent on the position and orientation of the director. Thus it has to be made sure that a director is uniquely defined at each node. Due to that it is important that the director is always pointing to one side of the shell surface.
A Full Example
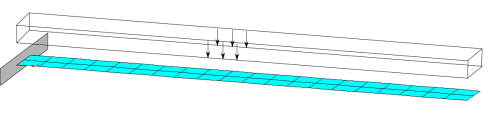
The following example describes a simple cantilever problem discretized by SHELL8 elements. The respective input file can be found here:
The problem computes three computation cases (dead load, snow load and pressure load). The boundary conditions are visualized by the figure below.
The basic goal of each linear static analysis is the computation of the displacement field. For load case 1 this result is depicted in the figure below, whereas the deformation in z-direction is additionally visualized by the color plot.
It can be seen that the support region does not show any deformation whereas the tip region deforms by a value of 8.76.
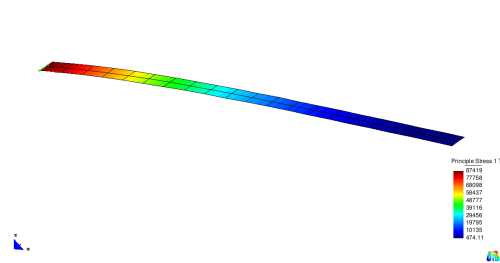
Often the stress distribution is visualized by color plots. Shell structures require the specification of the layer on which the stresses are computed. The picture below shows the first principle stress on the top of the cantilever.
It can be seen that the stresses show maximum values at the support region of the cantilever. At the tip they are nearly zero. In contrast to analytical results the stresses are not exactly zero in numerical models. The reason is the stress computation at the Gauss points. These points are situated inside the elements and not exactly at the tip of the cantilever.
References
- ↑ Linhard, J.; Wüchner, R.; Bletzinger K.U.: "Upgrading" membranes to shells — The CEG rotation free shell element and its application in structural analysis, Finite Elements in Analysis and Design, Elsevier, volume 44, pages 63-74, 2007
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedBi99
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |