Users:General FEM Analysis/Analyses Reference/Dynamic Analysis
| Line 266: | Line 266: | ||
|[[File:CantileverStructure.png|frame|up|Cantilever strcuture discretized with shell8-Elements]] | |[[File:CantileverStructure.png|frame|up|Cantilever strcuture discretized with shell8-Elements]] | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
The system shows an oscillation in the first Eigenform. The displacement versus timestep diagram is given in the figure below. | The system shows an oscillation in the first Eigenform. The displacement versus timestep diagram is given in the figure below. | ||
| + | {| | ||
| + | |[[File:DispVsIter.png|frame|up|Displacement Versus Timesteps at the tip of the Cantilever]] | ||
| + | |} | ||
Revision as of 13:57, 7 September 2010
Contents |
General Description
The dynamic analysis is used to analyze the time-dependent or transient behavior of structures. There exist various analysis types with different time integration algorithms and geometric linear and nonlinear formulations to cover small and large structural displacements.
Discretization in Space
The unknown variables used to describe the transient behavior of a structure are the displacement d, the velocity v and the acceleration a. The discretization in space by the Finite Element Method (FEM) leads to the general form of the linear equation of motion:
M a(t)+C v(t)+K d(t)=f(t)
with M as the mass matrix, C as the damping matrix, K as the linear stiffness matrix and f as the external and time-dependent force vector. It has to be noted, that the unknown variables are time-dependent.
Discretization in Time
For the discretization in time a time integration algorithm is used. The discretization is done in two steps. First, the examined time period t=[t0, ttot] is subdivided into discrete intervalls [tn, tn+1] and corresponding time steps Δtn=tn+1-tn. Seccond, for the progress of the variables within a timestep certain assumptions are made, depending on the choosen time integration algorithm. The solution is then only computed at discrete times. In Carat++ implicit time integration algorithms are used, which satisfy dynamic equilibrium at time n+1. Now, the system has the form:
M an+1+C vn+1+K dn+1=fn+1
This is an equation system with ndof equations, but 3 x ndof unknowns.
Linear Equation System
The chosen time integration algorithm allows a reduction to ndof equations, so it makes the system solvable. The acceleration and velocity can be formulated depending on the displacements only, so the main variable is the displacement. Using e.g. the Newmark-beta method leads to the following linear equation system:
(1/βΔt2 M + γ/2Δt C + K) dn+1=fn+1 + M(1/βΔt2dn + 1/βΔt vn + ...) +C(-vn- (1-γ)Δt an+...)
This system is solved in every timestep. All terms on the right hand side are already known and the system can be solved for the unknown displacements dn+1. After this, the corresponding velocity and acceleration are determined by backsubstitution.
Time Integration Methods
There are currently two time integration methods implemented:
- Newmark-beta method,
- Generalized-alpha method.
The Newmark-beta method uses two control parameters, β and γ. The choice of these parameters influences the accuracy and stability of the algorithm. Accuracy of 2nd order is given for β=0.25 and γ=0.5. Dissipation of higher frequencies is reached for γ≥0.5, but the accuracy is diminished to 1st order. Unconditional stability is guaranteed for a combination that ensures 2β≥γ≥0.5.
The Generalized-alpha method is based on the Newmark-beta method, but the equilibrium condition is formulated between two timesteps by linear blending. It uses four control parameters, β and γ from the Newmark-beta method and additionally the two linear shift-parameters αm and αf. The advantage of the Generalized-alpha method is to ensure 2nd order accuracy with controllable damping of higher frequency modes. The control parameters depend on the wanted damping of the higher frequencies, which is described by the spectral radius ρ∞. For ρ∞=1.0 no damping occurs, for ρ∞<1.0 higher frequencies are damped. An overview on parameter combinations is given in the following table. Other values can be found in the corresponding literature.
| Parameter Combination for Generalized-Alpha Method | ||||
| Spectral radius ρ∞ | β | γ | αm | αf |
|---|---|---|---|---|
| 1.0 | 0.250 | 0.500 | 0.500 | 0.500 |
| 0.9 | 0.277 | 0.553 | 0.421 | 0.474 |
| 0.8 | 0.309 | 0.611 | 0.333 | 0.444 |
Geometric Linearity and Nonlinearity
Choosing the algorithm decides whether a geometric linear or nonlinear formulation is used. Whereas the geometric linear formulation allows a solution within one iteration per timestep, the nonlinear formulation is based on a residuum formulation, a linearization and an iterative Newton method. So for a nonlinear analysis, in addition the maximum number of Newton iterations and the maximum norm of the residual force vector for the convergence proof has to be specified.
Rayleigh Damping
The damping term C v is velocity proportional and depends on the damping matrix C, which represents the influence of internal friction. This influence is typically not covered within the classical finite element derivation, but there exist other methods to determine a damping matrix. In Carat++ the so-called Rayleigh damping is implemented, which determines the damping matrix as a linear combination of the mass and stiffness matrix: C = α1M + α2K. The linear coefficients α1 and α2 are problem-dependent and can be determined from experiments.
Loading and Load Curves
The external load, which has to be specified, is time-dependent. To handle this in Carat++, one or more load curves have to be defined and combined with nodal and element loads. It is possible to specify e.g. one load curve for self-weight, another load curve for some single nodal loads and a third load curve for wind. The load curves consist of a list of discrete pairs of time and value. At least two time instances have to be specified. Between the time instances linear interpolation is used. Therefore, it is not necessary, that time instances of the load curve and computed times of the dynamic analysis match. It is only necessary, that the computed time interval is covered by all specified load curves.
Initial Load
An Initial Load exists, if the external loading at start time is not equal to zero. This may be case, if e.g. the loading consists of constant self-weight and a time-varying nodal load. If this is the case, an initial static solution is carried out and used as starting point for the dynamic analysis.
Restart Functionaliy
A Restart Functionality is implemented in Carat++, which allows to continue a dynamic computation from a certain time instance. It is useful in some cases:
- On cluster computing systems, typically computing time restrictions exist. The restart functionality allows to continue the computation from an already reached time instance.
- Very long and nonlinear computations with large displacements may show convergence problems and diverge. The restart functionality allows to perform a restart from an already computed level and adapt the solution approach, e.g. by diminishing the time step size, changing the time integration algorithm or introducing
The restart functionality consists of two parts. First, information necessary for a restart is written with a certain frequency into files with a certain name. Different time instances are stored to be able to restart not only from the last level, but also from an earlier level. Second, if a restart is performed, the starting time of the restart has to be specified. There will always exist two restartfiles, which are filled alternating.
Input Parameters
Parameter Description
| Compulsory Paramters | ||
| PC-ANALYSIS | int: DYNAMIC | Keyword of dynamic analysis with analysis ID |
|---|---|---|
| SOLVER | PC-SOLVER int | Linking to a linear solver |
| STARTTIME | float | Starttime of simulation |
| ENDTIME | float | Endtime of simulation |
| TIMESTEP | float | Timestep of simulation |
| OUTPUT | PC-OUT int | Link to output object |
| COMPCASE | LD-COM int | Link to computation case |
| DOMAIN | EL-DOMAIN int | Link to domain object |
| ALGORITHM | NEWMARK_LIN or NEWMARK_NLN or GENALPHA_LIN or GENALPHA_NLN | choose the time integration algorithm and linear or nonlinear gemoetry |
| BETA | float | Parameter β in Newmark-beta and Generalized-alpha method |
| GAMMA | float | Parameter γ in Newmark-beta and Generalized-alpha method |
| ALPHA_M | float | Parameter αm in Generalized-alpha method |
| ALPHA_F | float | Parameter αf in Generalized-alpha method |
| MAX_ITER_EQUILIBRIUM | int | Maximum number of Newton iterations to reach convergence - only for geometric nonlinear analysis |
| EQUILIBRIUM_ACCURACY | float | L2-norm of the residual as convergence proof - only for geometric nonlinear analysis |
| Optional Parameters for Rayleigh Damping | ||
| DAMPING | 0 or 1 | Add Rayleigh damping matrix to system |
| A1 | float | Parameter α1 |
| A2 | float | Parameter α3 |
| Optional Parameters for Restart | ||
| RESTARTRUN | 0 or 1 | Perform restart from STARTTIME, read restart information from file with prefix RESTARTFILEPREFIX |
| RESTARTOUTPUT | 0 or 1 | Write restart info to file with prefix RESTARTFILEPREFIX every RESTARTFREQUENCY steps |
| RESTARTFREQUENCY | int | Frequency of timesteps to write restart info to RESTARTFILEPREFIX |
| RESTARTFILEPREFIX | string | Write restart info to or read from files with names RESTARTFILEPREFIX.restart_1 and .restart_2 |
| RESTARTINFOINSTANCES | int | Keep restart information from RESTARTINFOINSTANCES in files, until info is overwritten |
Example of a Complete Input Block
PC-ANALYSIS 2: DYNAMIC SOLVER = PC-SOLVER 1 STARTTIME = 0.0 ENDTIME = 2.0 TIMESTEP = 0.0001 ALGORITHM = NEWMARK_NLN BETA = 0.25 GAMMA = 0.50 ALPHA_M = 0.50 ALPHA_F = 0.50 OUTPUT = PC-OUT 1 COMPCASE = LD-COM 1 DOMAIN = EL-DOMAIN 1 MAX_ITER_EQUILIBRIUM = 25 EQUILIBRIUM_ACCURACY = 0.00000001 DAMPING = 1 A1 = 2.709094 A2 = 0.000441 RESTARTRUN = 0 RESTARTOUTPUT = 1 RESTARTFREQUENCY = 10 RESTARTFILEPREFIX = restartfile RESTARTINFOINSTANCES = 3
Example of a Load Curve
LD-CURVE 1 TYPE=DISCRETE TIME=0.000 VAL=0.000 TIME=0.500 VAL=1.000 TIME=2.000 VAL=9.000
Example
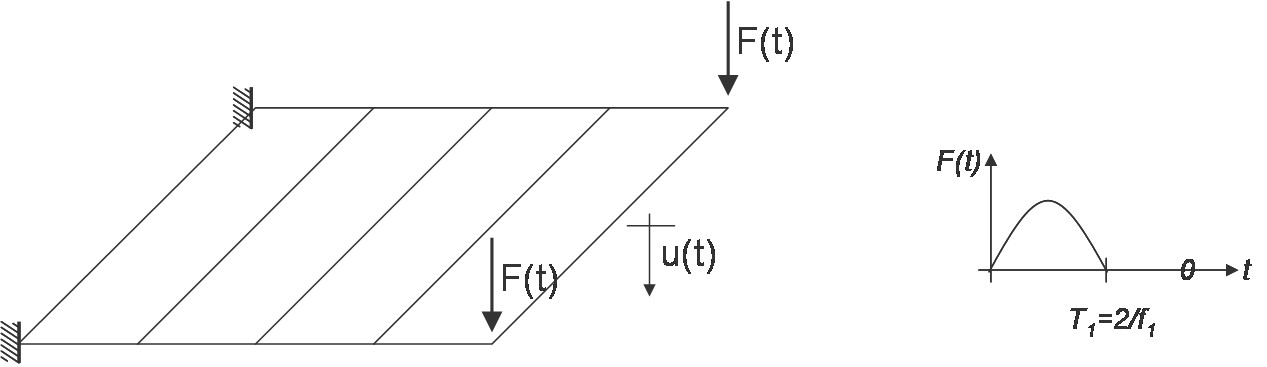
The following simple example shows a dynamic and geometric nonlinear analysis of a cantilever arm using the onlinear Newmark-beta method. The respective input file can be found in the SVN repository under
carat20/examples/benchmark_examples/analyses/dynamic_nonlinear_newmark_shell8_I/dynamic_nonlinear_newmark_shell8.txt.txt
The cantilever structure is modeled by four shell8-elements. Two single loads are applied on the tip perpendicular to the system area. The system is excited by a half-sinus.
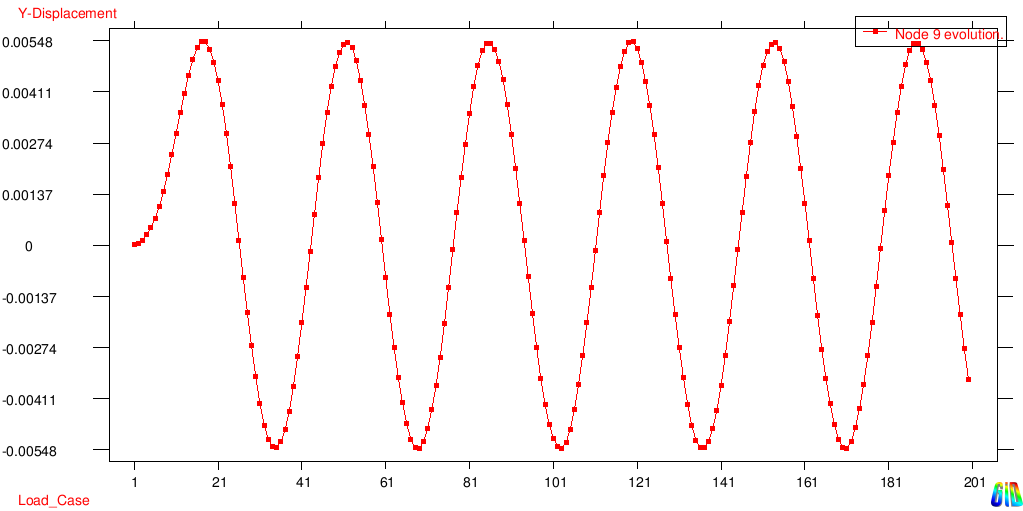
The system shows an oscillation in the first Eigenform. The displacement versus timestep diagram is given in the figure below.
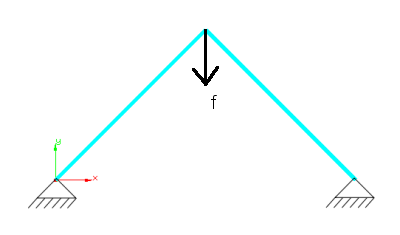 Simple 2bar truss structure discretized with truss elements |
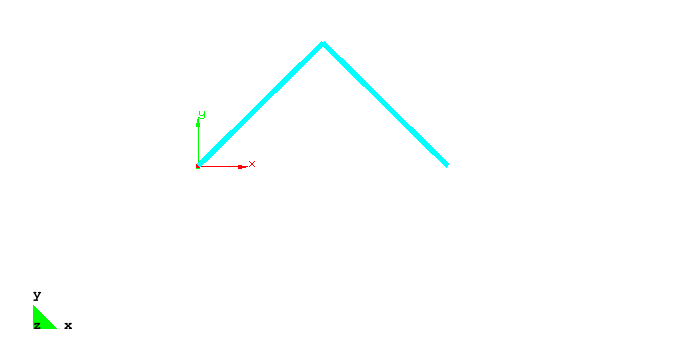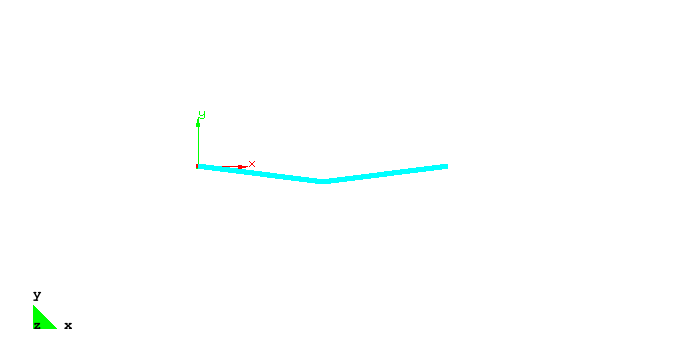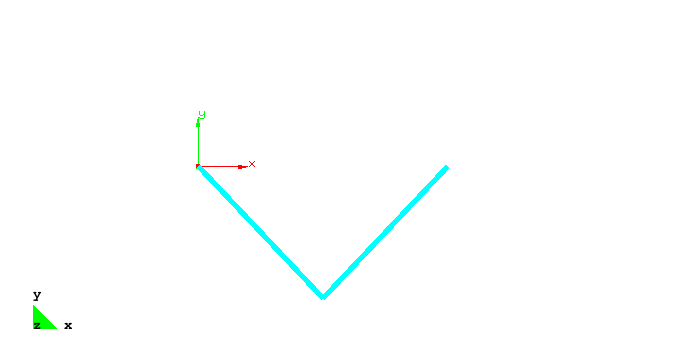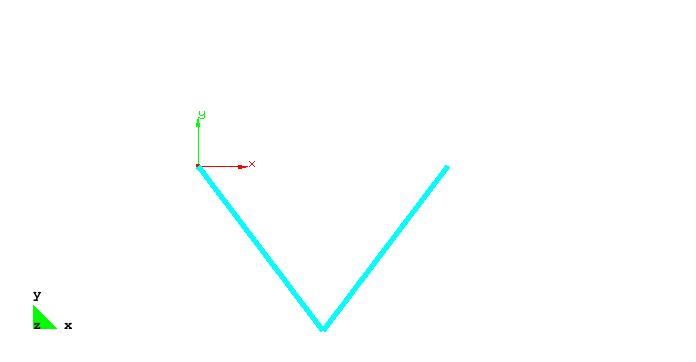
The load f is increased by the arclength method such that the displacements depicted in the figure below occur.
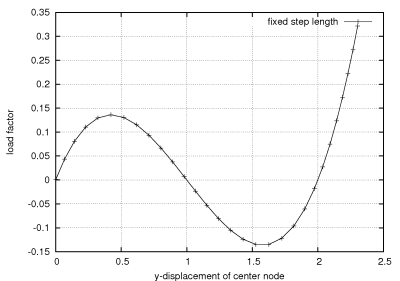
The figure below shows the load displacement path of the y-displacement of the center node. The well known snap through behavior is clearly visible. For a load factor of approx. 0.14 the structure shows instability. In the following the arclength control reduces the load factor until -0.14 to compute equilibrium states. Obviously these states can be only be computed by arclength or displacement control. After a complete snap through the load can be increased further. Now the complete structure works in tension which does not yield to further instability points.
References
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |