Users:Form Finding/Discussion of the Prestress State

From Carat++ Public Wiki
(Difference between revisions)
Jump to: navigation, search
Line 1: Line 1:
−
The main value in the ''URS'' is the prestress state. If the prestress don't match to the given problem there are no physical solution. So it can be seen, that the problem of finding the right prestress state is the main difficulty in the ''URS''. For a lot of sufaces an isotropic prestress state (σ<sub>11</sub> = σ<sub>22</sub> and σ<sub>12</sub>=0) is valid. But there are surfaces were an isotropic prestress state don't fit to the physics. The most popular kind of surface were an isotropic prestress state don't lead to a solution is the ''Chinese Hat'' (see figure below<ref name="Ish95">Ishii, K.: Membrane structures in Japan, SPS Publishing Company, Tokyo, 1995</ref>).
+
The main value in the ''URS'' is the prestress state. If the prestress does not match the given problem there is no physical solution. So it can be seen, that the problem of finding the right prestress state is the main difficulty in the ''URS''. For many surfaces an isotropic prestress state (σ<sub>11</sub> = σ<sub>22</sub> and σ<sub>12</sub>=0) is valid. But there are surfaces where an isotropic prestress state does not fit to the physics. The most popular kind of surface where an isotropic prestress state does not lead to a solution is the ''Chinese Hat'' (see figure below<ref name="Ish95">Ishii, K.: Membrane structures in Japan, SPS Publishing Company, Tokyo, 1995</ref>).
  
 
[[File:Chinese hat.jpg|400px|up|Chinese hat]]  
 
[[File:Chinese hat.jpg|400px|up|Chinese hat]]  
  
  
−
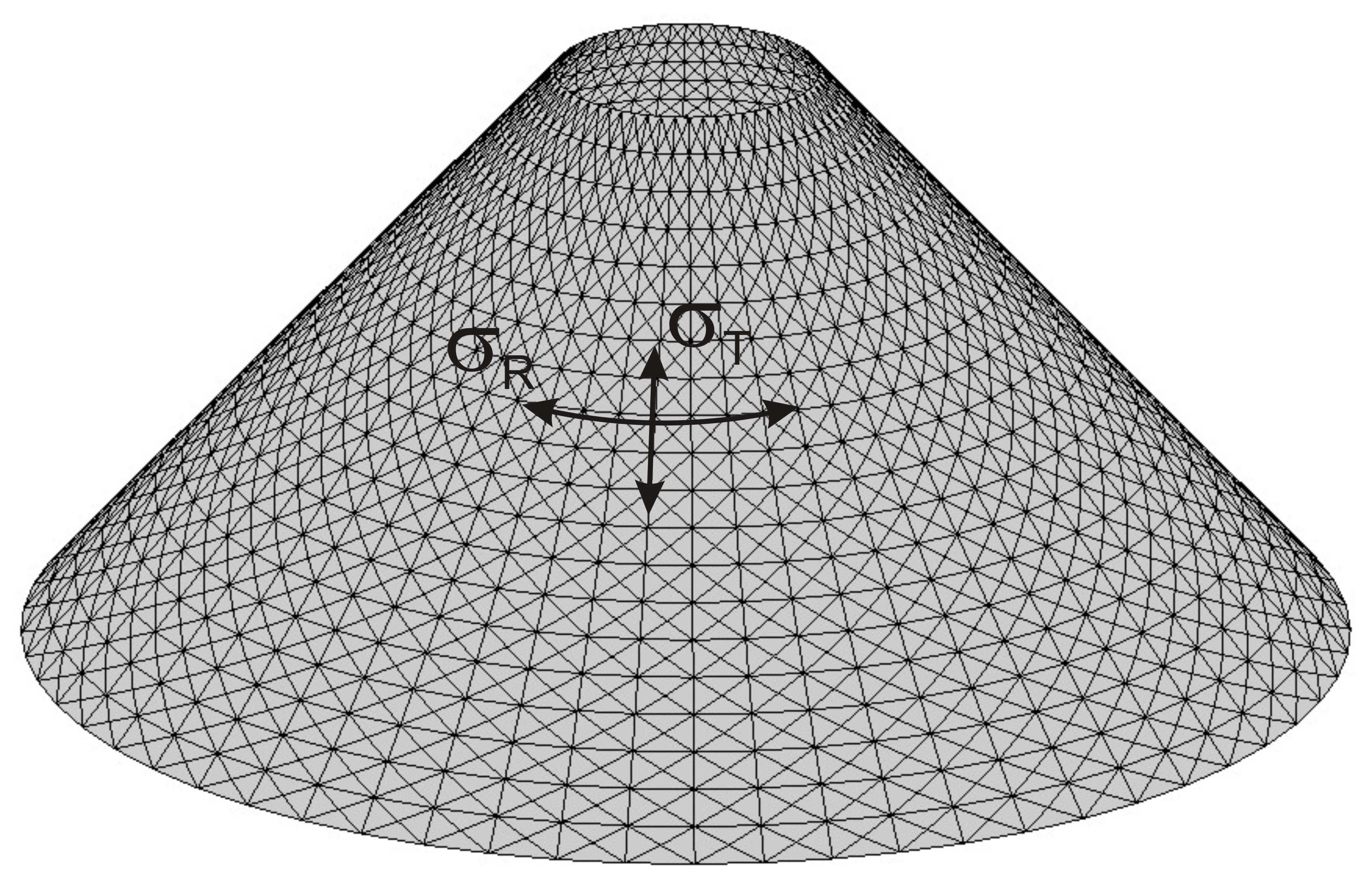
In figure below the definition of the stress dircetion of the chinese hat are shown.   
+
In the figure below the definition of the stress directions of the chinese hat are shown.   
  
 
[[File:Directions chinese hat.jpg|400px|up|Directions chinese hat]]  
 
[[File:Directions chinese hat.jpg|400px|up|Directions chinese hat]]  
  
−
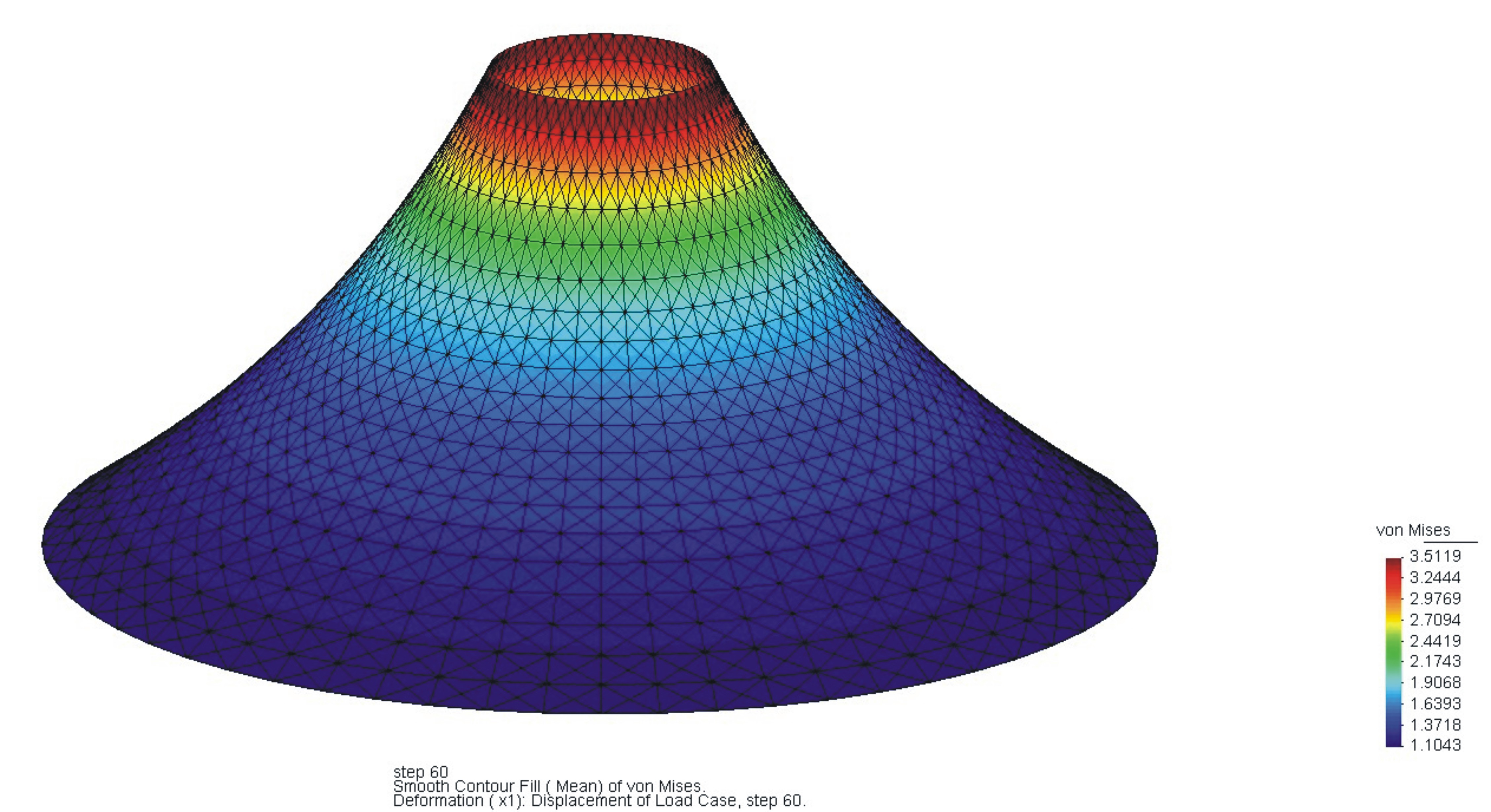
By using an isotropic stess state the nono physical solution for the ''Chinese Hat'' can be seen in Figure below.
+
By using an isotropic stess state the non physical solution for the ''Chinese Hat'' can be seen in figure below.
  
 
[[File:Iso chinese hat.jpg|400px|up|Iso chinese hat]]
 
[[File:Iso chinese hat.jpg|400px|up|Iso chinese hat]]
  
−
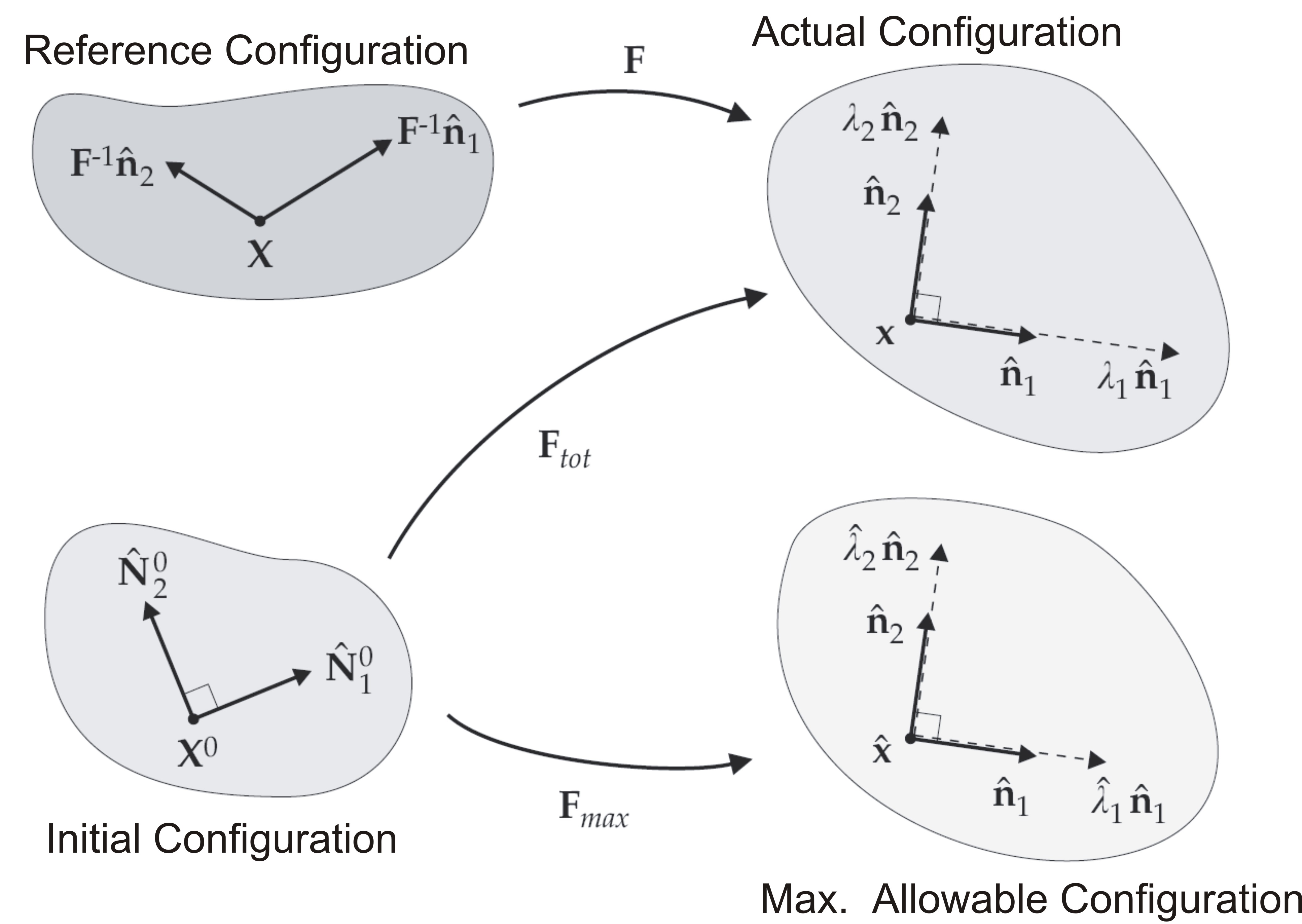
To enable the ''form finding'' to find the physical solution for such kind of structures, the possibility of stress adaption is used. By controlling the element distortion an adaption of the prestress in each Gauss point is possible. Herein the element distortion is controlled w.r.t. the principal stretch of an element (see figure below).
+
To enable the ''form finding'' to find the physical solution for these kinds of structures, the possibility of stress adaption is used. By controlling the element distortion an adaption of the prestress in each Gauss point is possible. Herein the element distortion is controlled w.r.t. the principal stretch of an element (see figure below).
  
 
[[File:Principal directions.jpg|400px|up|Principal directions]]
 
[[File:Principal directions.jpg|400px|up|Principal directions]]

Revision as of 14:13, 20 March 2017

The main value in the URS is the prestress state. If the prestress does not match the given problem there is no physical solution. So it can be seen, that the problem of finding the right prestress state is the main difficulty in the URS. For many surfaces an isotropic prestress state (σ11 = σ22 and σ12=0) is valid. But there are surfaces where an isotropic prestress state does not fit to the physics. The most popular kind of surface where an isotropic prestress state does not lead to a solution is the Chinese Hat (see figure below[1]).

Chinese hat


In the figure below the definition of the stress directions of the chinese hat are shown.

Directions chinese hat

By using an isotropic stess state the non physical solution for the Chinese Hat can be seen in figure below.

Iso chinese hat

To enable the form finding to find the physical solution for these kinds of structures, the possibility of stress adaption is used. By controlling the element distortion an adaption of the prestress in each Gauss point is possible. Herein the element distortion is controlled w.r.t. the principal stretch of an element (see figure below).

Principal directions

In the distortion control scheme a maximum allowable configuration is defined. That means, the initial configuration a maximum of displacement is allowed with a maximum deformation gradient Fmax. This configuration is the maximum allowable. During the form finding process the actual configuration is compared with the maximum allowable one. If the distortion is too much, the prestress will be modified in that way, that the maximum of distortion is kept in the allowable values. With this control scheme the Chinese Hat is possible to control and to get a physical meaningful solution (see figur below). But it should be noticed, that the final stress state isn't identical to the choosen one. Due to the choice of λ_max the stress is more or less different to the choosen one.

Solution chinese hat

For a more detailed discussion, refer also to [2] and [3].

References

  1. ↑ Ishii, K.: Membrane structures in Japan, SPS Publishing Company, Tokyo, 1995
  2. ↑ Linhard, J.: Numerisch-mechanische Betrachtung des Entwurfsprozesses von Membrantragwerken, Lehrstuhl für Statik, Technische Universität München, 2009
  3. ↑ Dieringer, F.: Numerical Methods for the Design and Analysis of Tensile Structures, Lehrstuhl für Statik, Technische Universität München, 2014




Whos here now:   Members 0   Guests 0   Bots & Crawlers 1
 
Retrieved from "http://carat.st.bv.tum.de/caratuserswiki/index.php/Users:Form_Finding/Discussion_of_the_Prestress_State"
Personal tools
Content for Users
Content for Developers