Users:General FEM Analysis/Analyses Reference/Static Nonlinear
| Line 188: | Line 188: | ||
The following simple example shows a geometrically nonlinear analysis of a 2bar truss system using the arclength method. It uses a fixed step size for computation. | The following simple example shows a geometrically nonlinear analysis of a 2bar truss system using the arclength method. It uses a fixed step size for computation. | ||
| − | The respective input file can be found in the | + | The respective input file can be found in the repository under |
| − | + | ||
| − | + | * ..\examples\benchmark_examples\analyses\stanln_2bartruss_arclength_l\2bartruss_arclength_fixed.txt | |
| − | + | ||
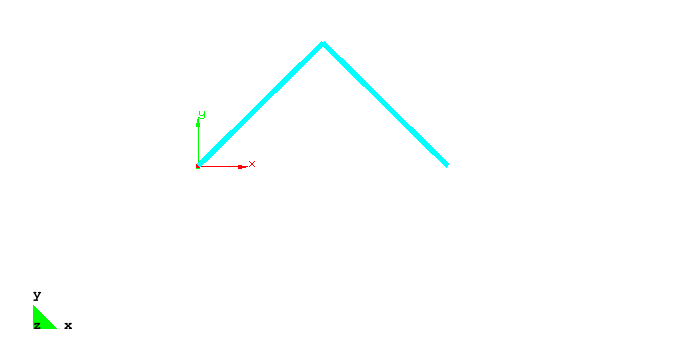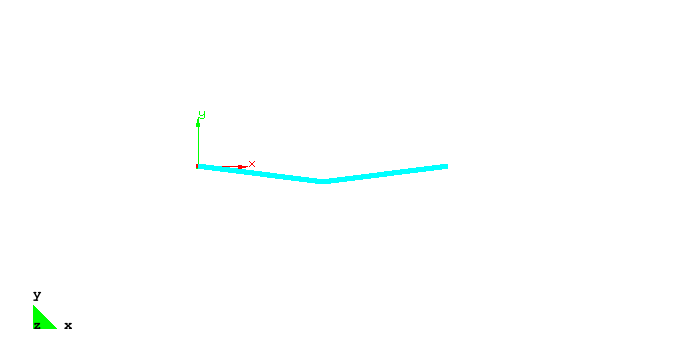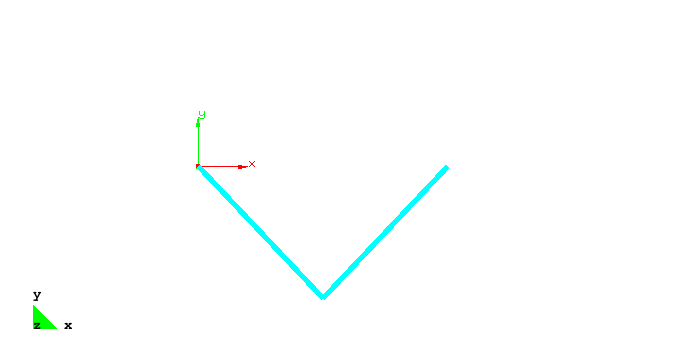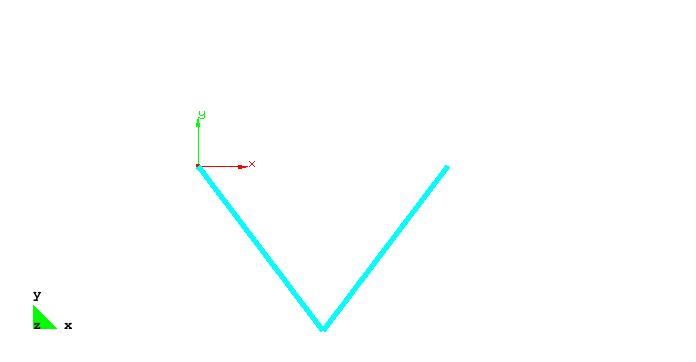
The problem computes a snap through problem. The [[Users:General FEM Analysis/BCs Reference|boundary conditions]] are visualized by the figure below. | The problem computes a snap through problem. The [[Users:General FEM Analysis/BCs Reference|boundary conditions]] are visualized by the figure below. | ||
{| | {| | ||
Revision as of 07:34, 7 December 2016
Contents |
General Description
The static nonlinear analysis is applied to analyze displacements, strains or stresses of nonlinear structures. There exists several sources of nonlinearities like nonlinear kinematics, nonlinear material behavior or contact scenarios.
The static nonlinear analysis formulates structural equilibrium on the actual configuration under consideration of the actual system response.
Structure of Equation System
A nonlinear problem is formulated by the equation r = f_int(u) - λ * f_ext(u) where r specifies the residual vector and f_int and f_ext define the internal and external forces, respectively. In general, the internal forces as well as the external forces depend on the actual displacement field u. Thus, the equation is nonlinear with respect to the a priori unknown equilibrium displacements. The parameter λ specifies a scaling parameter for the external load. Usually this parameter is controlled by a load curve which specifies λ as a function of the pseudo time t. The slope of this load curve must be small enough such that convergence is possible in each step. Whenever a nonlinear analysis has convergence problems it is appropriate to reduce the slope of this load curve and calculate more time steps.
At the equilibrium point the internal forces are equal to the external forces and the residual vector is equal to zero. The above specified nonlinear problem is linearized for the actual displacement state and solved by a Newton-Raphson scheme where the residual vector is used to compute incremental displacements by K_t u_inc = r. Here the tangential stiffness matrix is specified by K_t whereas u_inc denotes the incremental displacements.
Path Following Methods
The iterative solution of the nonlinear problem requires path following methods. The most simple path following method is a pure Load Control. Here the parameter λ (lambda) is increased according to the specified load curve. This allows nonlinear analysis for relatively robust nonlinear problems. But as soon as the structure shows instabilities the load control method usually does not not converge anymore. In this case the arc length method can be applied to compute the equilibrium path. This method controls the so called arc length which is defined as a combination of displacement increment and load increment. In general it is also possible to directly control a specified displacement.
More information about path following methods can be found e.g. in the theses of Reiner Reitinger[1] and Amphon Jarusjarungkiat[2].
Step Length Control
Actually there exist two methods for step length control in Carat++. The most simple method is the fixed step length which computes the whole load displacement path with a constant step length. This procedure is robust but inefficient because a large number of load steps has to be computed. Usually it is more efficient to apply adaptive step length methods. A very robust method was presented by Crisfield and Ramm, cf. [1]. This method specifies the actual step length for the time step i by the operation
StepLength_i = alpha * StepLength_i-1.
The parameter alpha is computed by (J_d / (J_i-1 * (Nmb_Restarts+1)))^p with: J_d = desired number of equilibrium iterations, J_i-1 = equilibrium iterations of last time step and p equals the exponent.
Example: Actual iteration step: i
Number of desired equilibrium iterations: J_d = 8.
Number of equilibrium iterations in the last time step: J_i-1 = 12.
Number of restarts: Nmb_Restarts = 0.
Exponent: p=1.0.
Step length of last step: StepLength_i-1 = 0.2.
alpha = ( 8 / (12*(0+1)))^(1.0) = (8 / 12)^(1.0) = 2/3.
StepLength_i = 2/3 * 0.2 = 0.1333.
Thus, if the number of equilibrium iterations is larger than a desired value the step length is decreased for the next time step. If the number of equilibrium iterations is smaller than a desired value the step length is increased for the next time step. The exponent p can be used to manipulate the update speed. It should be used with care.
Simultaneous Eigenvalue Analysis
Reaching critical points of the load displacement path (limit points, bifurcation points, ...) requires special investigations. A simultaneous eigenvalue analysis solving the problem
(K_t - eigenvalue * I) phi = 0
allows for approximation of the load factor at the next critical point lambda_k. Whenever a critical point is reached the above equations yields a zero eigenvalue. Extrapolating the current load factor according to the eigenvalue allows for good approximations of the critical load.
Imperfect Designs
Many structures subjected to large compression loading are sensitive to geometrical imperfections. Unfortunately the shape of the imperfection is a priori unknown but mostly some information about tolerances exist. In the nonlinear analysis the imperfection shapes can be computed as sum of several normalized eigenmodes. The final imperfection mode is then scaled by the specified tolerance. This operation can be expressed by
dx_imp = tol * (sum_i phi_i).
After computation of the imperfection mode, the geometry of the structure is modified and the nonlinear analysis starts with the imperfect geometry.
Input Parameters
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| PC-ANALYSIS | int : STA_GEO_NONLIN | Keyword of nonlinear analysis with analysis ID |
| PATHCONTROL | FORCE or ARCLENGTH or DISPLACEMENT | Definition of path control method. |
| SOLVER | PC-SOLVER int | Linking to a linear solver (direct or iterative) |
| OUTPUT | PC-OUT int | Linking to output objects (specifies the type of output format, e.g. GiD) |
| COMPCASE | LD-COM int | Linking to computation case object which specifies the boundary conditions (loading and supports). Only a single computation case is allowed. |
| DOMAIN | EL-DOMAIN int | Linking to the domain the analysis should work on. |
| NUM_STEP | int | Number of (pseudo) time steps that have to be calculated. |
| MAX_ITER_EQUILIBRIUM | int | Maximum number of equilibrium iterations that are allowed per (pseudo) time step. |
| EQUILIBRIUM_ACCURACY | float | Equilibrium accuracy that has to be reached for convergence. The convergence is checked with the L2 norm of the incremental displacements. |
| CURVE | LD-CURVE int | Linking to the load curve. |
| Optional Parameters | ||
| TRACED_NODE | int | Node ID of traced node. Used for screen and log file output. |
| TRACED_NODAL_DOF | dof type | DOF type of node TRACED_NODE that is traced (DISP_X, DISP_Y, DISP_Z, ...). |
| STEP_LENGTH_CONTROL | FIXED or CRISFIELD_RAMM | Type of step length control algorithm (only for ARCLENGTH method).
FIXED specifies a constant step size where the desired step size is defined by the parameter STEP_LENGTH_CONTROL_REALS. CRISFIELD_RAMM specifies an adaptive method according to Crisfield and Ramm, c.f. [1]. In this case the parameter STEP_LENGTH_CONTROL_INTS = int specifies the number of restarts that are allowed. The other necessary parameters are specified by STEP_LENGTH_CONTROL_REALS. See the example below. |
| STEP_LENGTH_CONTROL_REALS | float, float, ... | respective number of floats for step length control algorithm |
| STEP_LENGTH_CONTROL_INTS | int, int, ... | respective number of integers for step length control algorithm |
| SIMULTANEOUS_EIGENVALUE_ANALYSIS | 1 or 0 | flag to specify if a simultaneous eigenvalue analysis should be performed:
0 - no eigenvalue analysis 1 - perform eigenvalue analysis. This flag requires definition of parameter EIGEN_SOLVER. |
| EIGEN_SOLVER | PC-SOLVER int | Linking to an eigenvalue solver |
| IMPERFECTION_MODES | int, int, int, ... | specifies which eigen modes should be summarized to the imperfection mode. Computation of imperfect design requires definition of parameter EIGEN_SOLVER. |
| IMPERFECTION_SIZE | float | specifies the scalingof the imperfection mode. |
Example of a Complete Input Block
PC-ANALYSIS 1: STA_GEO_NONLIN
PATHCONTROL = ARCLENGTH ! or DISPLACEMENT or ARCLENGTH
SOLVER = PC-SOLVER 1
OUTPUT = PC-OUT 1
COMPCASE = LD-COM 1
DOMAIN = EL-DOMAIN 1
NUM_STEP = 30
MAX_ITER_EQUILIBRIUM = 100
EQUILIBRIUM_ACCURACY = 1e-10
CURVE=LD-CURVE 1
TRACED_NODE=2
TRACED_NODAL_DOF=DISP_Y
! Example: fixed step length of 0.05
STEP_LENGTH_CONTROL = FIXED
STEP_LENGTH_CONTROL_REALS = 0.05 ! constant step length of 0.05
! Example adaptive step length according to Crisfield and Ramm
STEP_LENGTH_CONTROL = CRISFIELD_RAMM
STEP_LENGTH_CONTROL_REALS = 0.1, 1.0 ! initial step length = 0.1, exponent p = 1.0
STEP_LENGTH_CONTROL_INTS = 5 ! 5 equilibrium iterations per step are desired
! Example: no simultaneous eigenvalue analysis
SIMULTANEOUS_EIGENVALUE_ANALYSIS = 0
! Example: simultaneous eigenvalue analysis
SIMULTANEOUS_EIGENVALUE_ANALYSIS = 1
EIGEN_SOLVER = PC-SOLVER 2
! Example: use imperfect design with modes 1, 2, 4, and 6
IMPERFECTION_MODES = 1, 2, 4, 6
IMPERFECTION_SIZE = 0.015 ! maximum size of imperfection mode equals 0.015
EIGEN_SOLVER = PC-SOLVER 2
Example
The following simple example shows a geometrically nonlinear analysis of a 2bar truss system using the arclength method. It uses a fixed step size for computation. The respective input file can be found in the repository under
- ..\examples\benchmark_examples\analyses\stanln_2bartruss_arclength_l\2bartruss_arclength_fixed.txt
The problem computes a snap through problem. The boundary conditions are visualized by the figure below.
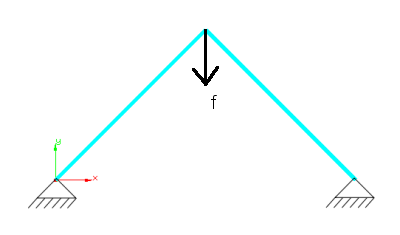 Simple 2bar truss structure discretized with truss elements |
The load f is increased by the arclength method such that the displacements depicted in the figure below occur.
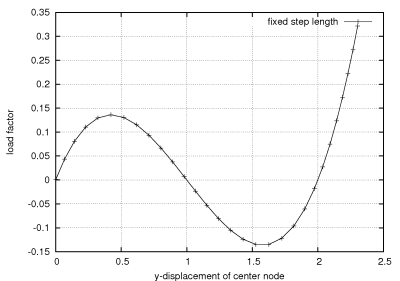
The figure below shows the load displacement path of the y-displacement of the center node. The well known snap through behavior is clearly visible. For a load factor of approx. 0.14 the structure shows instability. In the following the arclength control reduces the load factor until -0.14 to compute equilibrium states. Obviously these states can be only be computed by arclength or displacement control. After a complete snap through the load can be increased further. Now the complete structure works in tension which does not yield to further instability points.
References
- ↑ 1.0 1.1 1.2 Reitinger, R.: Stabilität und Optimierung imperfektionsempfindlicher Tragwerke, Dissertation, Bericht Nr. 17, Institut für Baustatik, Universität Stuttgart, 1994
- ↑ Jarusjarungkiat, A.: Nonlinear Analysis of Pneumatic Membranes - "From Subgrid to Interface", Dissertation, Lehrstuhl für Statik, Technische Universität München, 2009
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |