Users:General FEM Analysis/Analyses Reference/Cutting Pattern
(→Example) |
|||
| Line 98: | Line 98: | ||
== Example == | == Example == | ||
| − | The following simple example shows | + | The following simple example shows the cutting pattern analysis of two parts from a four-point sail. It uses a static relaxation method, the flattening area is the mean surface normal and a Galerkin approach is used for the patterning method. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{| | {| | ||
|[[File:2bar_truss_org.png|frame|up|Simple 2bar truss structure discretized with [[Users:General FEM Analysis/Elements Reference/Truss1|truss elements]]]] | |[[File:2bar_truss_org.png|frame|up|Simple 2bar truss structure discretized with [[Users:General FEM Analysis/Elements Reference/Truss1|truss elements]]]] | ||
Revision as of 15:27, 30 November 2016
Contents |
General Description
Cutting pattern generation determines a plane and (optimally) stress-free geometry which can be reassembled to build a membrane with a certain prestress and shape (as it was determined in Formfinding).
Structure of Equation System
A nonlinear problem is formulated by the equation r = f_int(u) where r specifies the residual vector and f_int defines the internal forces respectively. In general, the internal forces depend on the actual displacement field u. Thus, the equation is nonlinear with respect to the a priori unknown equilibrium displacements.
At the equilibrium point the residual vector is equal to zero. The above specified nonlinear problem is linearized for the actual displacement state and solved e.g. by a Newton-Raphson scheme where the residual vector is used to compute incremental displacements by K_t u_inc = r.
Input Parameters
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| PC-ANALYSIS | int : CUTTING_PATTERN | Keyword of analysis with analysis ID |
| SOLVER | PC-SOLVER int | Linking to a linear solver (direct or iterative) |
| OUTPUT | PC-OUT int | Linking to output objects (specifies the type of output format, e.g. GiD) |
| COMPCASE | LD-COM int | Linking to computation case object which specify the boundary conditions (loading and supports). Only a single computation case is allowed. |
| DOMAIN | EL-DOMAIN int | Linking to the domain the analysis should work on |
| MAX_ITER_EQUILIBRIUM | int | Maximum number of equilibrium iterations that are allowed. |
| EQUILIBRIUM_ACCURACY | float | Equilibrium accuracy that has to be reached for convergence. The convergence is checked with the L2 norm of the incremental displacements. |
| PATTERN | PART int | The parts which should be included in the analysis, separation with comma. |
| BC_CONFIGURATION | TYPE int | The type of boundary condition configuration, 4 means largest distance between the supports. For each part, one type must be given. |
| RELAXATION_METHOD | STATIC or NONE or GALERKIN or COMBINED | Definition of relaxation method. |
| FLATTENING_AREA | 0 or 1 | 0... prestress area. 1... mean surface normal. |
| PATTERNING_METHOD | GALERKIN or LS_NR or LS_CG or NONE | Definition of the patterning method. GALERKIN... principle of virtual work. LS_NR and LS_CG... optimization problem solved with Newton-Raphson or Conjugate Gradient approach. |
| Optional Parameters | ||
| SEAM_LENGTH | to be added | Includes the seam lengths into the cutting pattern analysis. |
Example of a Complete Input Block
PC-ANALYSIS 1: CUTTING_PATTERN DOMAIN = EL-DOMAIN 1 MAX_ITER_EQUILIBRIUM = 20 EQUILIBRIUM_ACCURACY = 1e-06 COMPCASE = LD-COM 1 OUTPUT = PC-OUT 1 PATTERN = PART 1,3 BC_CONFIGURATION = TYPE 4,4 SOLVER = PC-SOLVER 1 RELAXATION_METHOD=STATIC !NONE, STATIC, GALERKIN, COMBINED FLATTENING_AREA=1 !0 ...Prestress area, 1 ...Mean surface normal PATTERNING_METHOD=GALERKIN !LS_NR, GALERKIN, LS_CG, NONE
Example
The following simple example shows the cutting pattern analysis of two parts from a four-point sail. It uses a static relaxation method, the flattening area is the mean surface normal and a Galerkin approach is used for the patterning method.
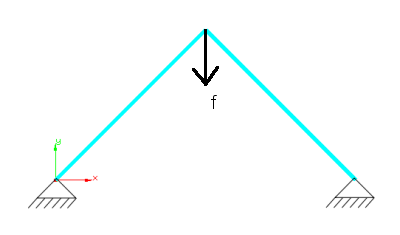 Simple 2bar truss structure discretized with truss elements |
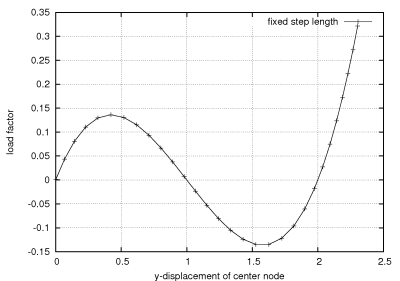
The load f is increased by the arclength method such that the displacements depicted in the figure below occur.
The figure below shows the load displacement path of the y-displacement of the center node. The well known snap through behavior is clearly visible. For a load factor of approx. 0.14 the structure shows instability. In the following the arclength control reduces the load factor until -0.14 to compute equilibrium states. Obviously these states can be only be computed by arclength or displacement control. After a complete snap through the load can be increased further. Now the complete structure works in tension which does not yield to further instability points.
References
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |