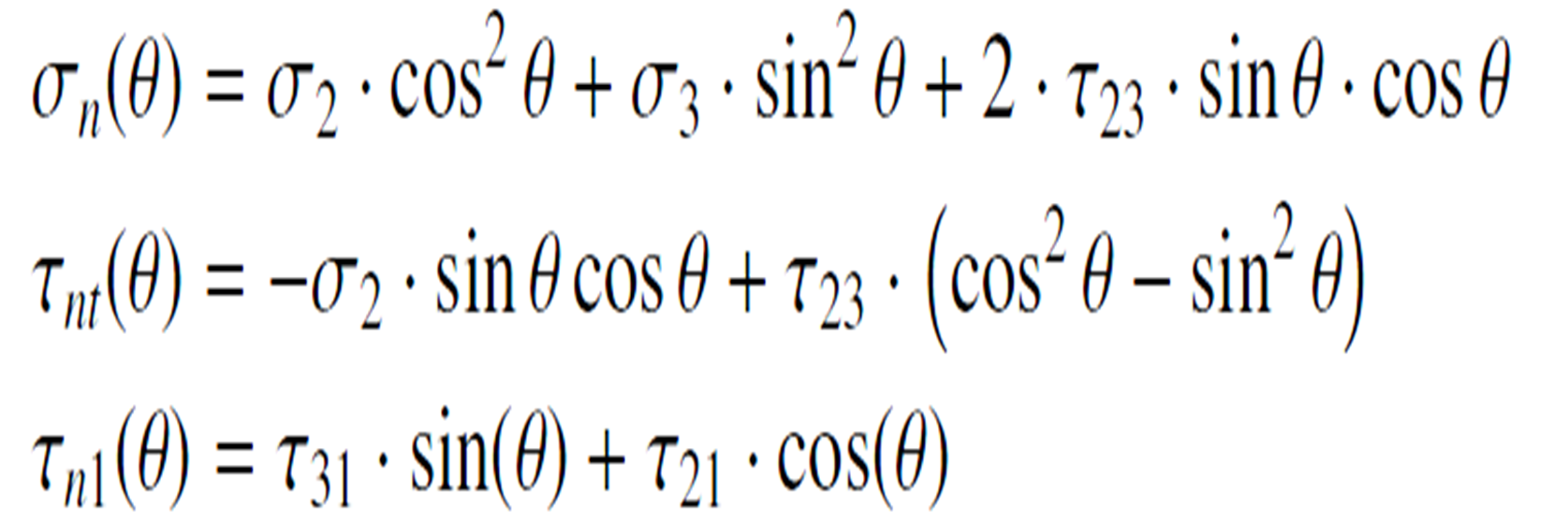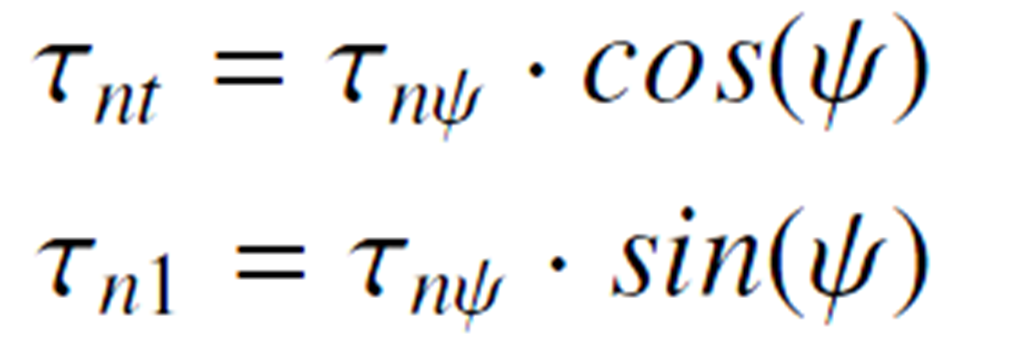Users:General FEM Analysis/Materials Reference/Puck Failure Criterion
From Carat++ Public Wiki
< Users:General FEM Analysis | Materials Reference(Difference between revisions)
| (3 intermediate revisions by one user not shown) | |||
| Line 2: | Line 2: | ||
== General Description == | == General Description == | ||
| − | + | Puck Failure Criterion | |
| + | <ref> | ||
| + | A. Puck: Festigkeitsanalyse von Faser-Matrix-Laminaten. Hanser, 1996. ISBN 3-446-18194-6 | ||
| + | </ref> | ||
| + | <ref> | ||
| + | H. Deuschle. 3D failure analysis of UD fibre reinforced composites: Puck’s theory within FEA. | ||
| + | Phd thesis, Universität Stuttgart, 2010. | ||
| + | </ref> | ||
| + | <ref> | ||
| + | M. Knops. Analysis of Failure in Fiber Polymer Laminates. Springer Berlin Heidelberg, Berlin, | ||
| + | Heidelberg, 2008. | ||
| + | </ref> | ||
| + | is based on Mohr‘s fracture hypothesis | ||
| + | <ref> | ||
| + | O. Mohr. Welche Umstände bedingen die Elastizitätsgrenze und den Bruch eines Materials? | ||
| + | (German). Zeitschrift des Vereins deutscher Ingenieure, 24:1524 ff, 1900. | ||
| + | </ref> | ||
| + | which is appropriate for brittle fracture behaviour of composite materials. It can distinguish between fibre fracture and different inter-fibre fracture. Both 2D and 3D formulations are implemented into Carat++. | ||
Available fracture modes for 2D Puck Criterion are: | Available fracture modes for 2D Puck Criterion are: | ||
* Fibre Fracture (FF) | * Fibre Fracture (FF) | ||
| Line 21: | Line 38: | ||
[[File:Figure 3.4.png|500px]] | [[File:Figure 3.4.png|500px]] | ||
| + | |||
| + | Stresses of the action plane | ||
| + | <ref> | ||
| + | M. Knops. Analysis of Failure in Fiber Polymer Laminates. Springer Berlin Heidelberg, Berlin, | ||
| + | Heidelberg, 2008. | ||
| + | </ref> | ||
| Line 56: | Line 79: | ||
[[File:puck.png|1000px]] | [[File:puck.png|1000px]] | ||
| + | <ref> | ||
| + | Altug Emiroglu, Master Thesis: Comparative Study of Puck and Tsai-Wu Failure Criteria, Technische Universität München, 2013. | ||
| + | </ref> | ||
| + | |||
== Parameter Description == | == Parameter Description == | ||
| Line 151: | Line 178: | ||
=== Example of a Complete Input Block === | === Example of a Complete Input Block === | ||
[[File:input_puck.png|500px]] | [[File:input_puck.png|500px]] | ||
| + | |||
| + | |||
| + | == References == | ||
| + | <references/> | ||
Latest revision as of 10:05, 15 February 2013
Contents |
General Description
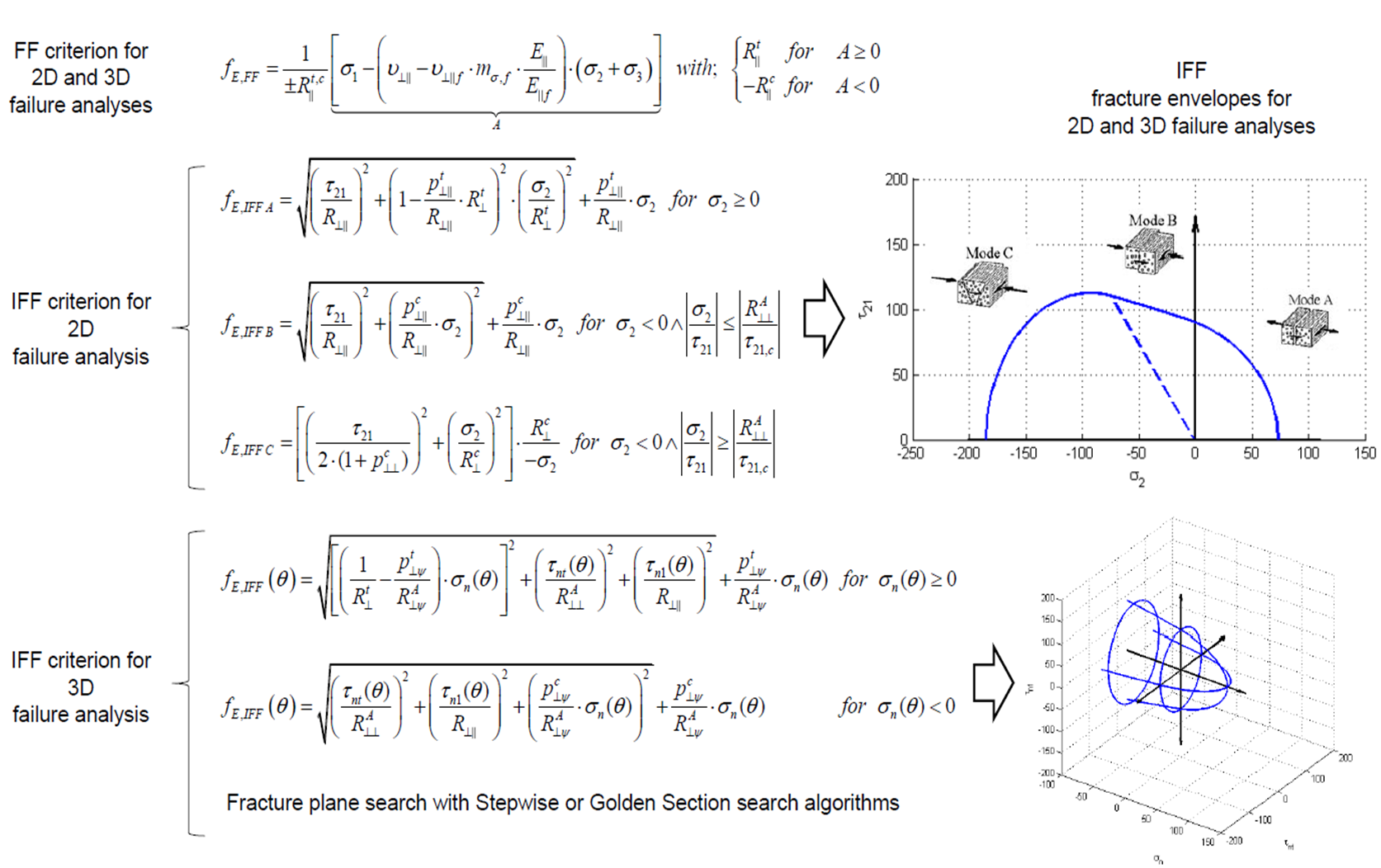
Puck Failure Criterion [1] [2] [3] is based on Mohr‘s fracture hypothesis [4] which is appropriate for brittle fracture behaviour of composite materials. It can distinguish between fibre fracture and different inter-fibre fracture. Both 2D and 3D formulations are implemented into Carat++. Available fracture modes for 2D Puck Criterion are:
- Fibre Fracture (FF)
- Inter Fibre Fracture Mode A (IFF A)
- Inter Fibre Fracture Mode B (IFF B)
- Inter Fibre Fracture Mode C (IFF C)
Available fracture modes for 3D Puck Criterion are:
- Fibre Fracture (FF)
- Inter Fibre Fracture (IFF)
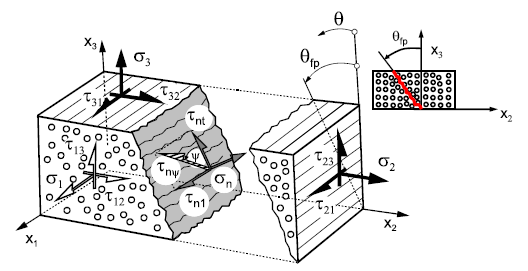
Stresses on the Fracture Plane
Stresses of the action plane [5]
Strength Analysis
In order to judge if a stress vector on the stress spce is leading to damage, a mathematical expression is needed. This expression is called fracture condition an is written as the following general form:
: Components of stress vector
Ri. : Strengths under corresponding stresses
F : Fracture function
There are 6 main strengths that should be related to the occurring stress state:
The general form of fracture condition can also be rewritten as following:
F < 1 : no fracture
F = 1 : fracture limit reached and fracture occurs
F > 1 : fracture limit exceeded
with F 
[0,
)
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| EF | real | Elasticity modulus of the fibres |
| RTL | real | Resistance to longitudinal tension (Direction 1) |
| RCL | real | Resistance to longitudinal compression (Direction 1) |
| RTT | real | Resistance to transverse tension (Direction 2) |
| RCT | real | Resistance to transverse compression (Direction 2) |
| RSL | real | Resistance to longitudinal shear |
| VFF | real | Volume fraction of the fibres |
| PTTL | real | Inclination parameter,
|
| PCTL | real | Inclination parameter,
|
| Optional Parameters | ||
| Parameter | Values, Default(*) | Description |
| STRESS TYPE | 2D, 3D | Indicates what kind of stress state should be used to calculate the failure condition. When not given, related element’s stress type is taken. |
| NUE12F | real | Poisson’s ratio for fibres. (De f ault = 0.2) |
| MGF | real | Amplification factor (De f ault = 1.2) |
| S, M | real | Parameters necessary for calculation of weakening due to  (De f ault = S = M = 0.5)
|
| PTT | real | Inclination parameter  . When not given, calculated using the strength values. See Section 3.1.2.3
|
| WEAKENING | int | Switch for calculation of weakening due to .
|
| FPS | SWS*, GSS | Switch for fracture plane search algorithm.
|
| FPS_SWS_SIZE | real | Step size for step-wise fracture plane search |
Example of a Complete Input Block
References
- ↑ A. Puck: Festigkeitsanalyse von Faser-Matrix-Laminaten. Hanser, 1996. ISBN 3-446-18194-6
- ↑ H. Deuschle. 3D failure analysis of UD fibre reinforced composites: Puck’s theory within FEA. Phd thesis, Universität Stuttgart, 2010.
- ↑ M. Knops. Analysis of Failure in Fiber Polymer Laminates. Springer Berlin Heidelberg, Berlin, Heidelberg, 2008.
- ↑ O. Mohr. Welche Umstände bedingen die Elastizitätsgrenze und den Bruch eines Materials? (German). Zeitschrift des Vereins deutscher Ingenieure, 24:1524 ff, 1900.
- ↑ M. Knops. Analysis of Failure in Fiber Polymer Laminates. Springer Berlin Heidelberg, Berlin, Heidelberg, 2008.
- ↑ Altug Emiroglu, Master Thesis: Comparative Study of Puck and Tsai-Wu Failure Criteria, Technische Universität München, 2013.
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |
