Users:General FEM Analysis/Elements Reference/BeamCR
(→Parameter Description) |
(→Use of the shear sections factors SHEAR_SECTION_Y and SHEAR_SECTION_Z) |
||
| Line 87: | Line 87: | ||
</pre> | </pre> | ||
| − | === Use of the shear sections | + | === Use of the shear sections SHEAR_SECTION_Y and SHEAR_SECTION_Z === |
| − | The shear | + | The shear sections ''SHEAR_SECTION_Y'' and ''SHEAR_SECTION_Z'' depend on the cross section of the beam and can be obtained by multiplying the area of the beam ''AREA'' with the shear correction factor α which is dependent on the shape of the sections. For a rectangle, α=5/6. |
=== Use of the rotation parameter THETA === | === Use of the rotation parameter THETA === | ||
Revision as of 16:26, 17 December 2015
Contents |
General Description
Element Type
- This beam element is a 2 node non-linear 3D-beam for large rotations and small deformations (Green-Lagrange-strains)taking into account shear deformation (Timoshenko-beam element).
- This beam element has 6 DOFs per node (three translations and three rotations)
- The stiffness matrix for the linear calculation is hard-coded, thus not needing any integration. For theory of 2nd order, the normal force in the element leads to modifications in the stiffness matrix.
Degrees of Freedom
For the Beam1 element use the 3 translatoric degrees of freedom DISP_X, DISP_Y, DISP_Z and the 3 rotatoric degrees of freedom ROT_X, ROT_Y, ROT_Z.
Theory of 2nd Order
If Theory of 2nd Order should be taken into account, a nonlinear calculation (ANALYSIS STA_GEO_NLIN) has to be executed.
Orientation of the local coordinate system
The Beam1 element uses the following definition for the determination of the local coordinate system (needed for the orientation of IYY and IZZ,...):
- the local x-axis is oriented from node 1 to node 2 of the beam
- the local y-axis lies in the global XY-plane, such that the local z-axis points in the same half-space as the global Z-axis (mathematically spoken: the local z-axis and the global Z-axis result in a positive dot-product)
- the local z-axis is perpendicular to the other two local axis, following the right-hand-rule for x-y-z
- exception: If the local x-axis (i.e. the beam axis) points in the direction of global Z, the local y-axis points in the direction of the global Y-axis. The local z-axis once again follows the right-hand-rule for x-y-z.
These coordinate systems have the role of a local Frenet-frame that is rotated with the element during a non-linear analysis.
In case that a rotation of the local coordinate system is needed (rotated elements, inverse definition of IYY and IZZ,...) an angle THETA has to be specified. This angle rotates the whole coordinate system around the local x-axis, following the right-thumb rule (i.e. the thumb of the right hand points in the direction of the local x-axis).
Update of the local coordinate system
For updating the local coordinate system, the element base vectors are rotated by a rotation of magnitude dφax of the anti-symmetric rotation increment dφa around the beam axis, followed by the rotation of the whole coordinate system to align the base vector nx with the update beam axis. The complete rotation of the base configuration is represented by a rotation matrix T which is defined by the current element base vectors T = [nx ny nz].
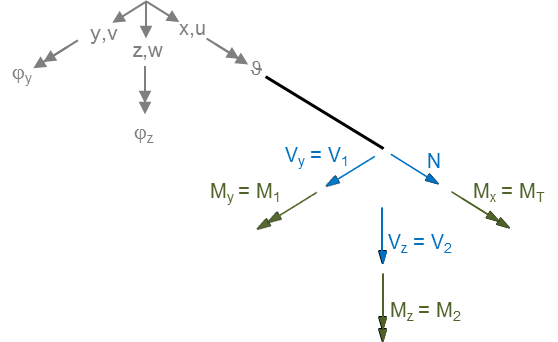
Orientation of the resultant forces
The BeamCR element has 6 resultant forces in accordance with the degrees of freedom. The resultant forces, [ N V1 V2 | MT M1 M2 ], are oriented along the local axes on the positive section of the beam. Note that the resultantforces are evaluated in the center of the beam element, so it's the mean value of the two ends. For the orientation, cf. also the orientation sketch:
Input Parameters
Parameter Description
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| MAT | EL-MAT int | Number for the used Material
e.g. MAT=EL-MAT 1 |
| AREA | Definition of the cross-sectional area of the beam | |
| IYY, IZZ | Definition of the moments of inertia | |
| Optional Parameters | ||
| IT | IT=IYY+IZZ | Definition of the torsional resistance |
| SHEAR_SECTION_Y, SHEAR_SECTION_Z | Definition of the shear-corss-sectional area of the beam in y- and z-direction | |
| THETA | 0 | Angle of rotation of the local coordinate system around the beam axis in degrees |
Example of a Complete Input Block
EL-PROP 1 : BEAM_CR MAT= EL-MAT 1 AREA=0.015 IYY=1.125 IZZ=0.03125 SHEAR_SECTION_Y=0.0075 SHEAR_SECTION_Z=0.015 THETA=90
Use of the shear sections SHEAR_SECTION_Y and SHEAR_SECTION_Z
The shear sections SHEAR_SECTION_Y and SHEAR_SECTION_Z depend on the cross section of the beam and can be obtained by multiplying the area of the beam AREA with the shear correction factor α which is dependent on the shape of the sections. For a rectangle, α=5/6.
Use of the rotation parameter THETA
The rotation parameter THETA and its use is explained in the section concerning the coordinate system above.
The torsional resistance IT
The torsional resistance IT is interpreted as the polar moment Ipp, i.e.: IT = Ipp = IYY + IZZ.
Element Loading
For the moment, only nodal forces in the three global directions can be applied (i.e. Fx, Fy, Fz).
Pressure
- not defined yet
Dead Load
- implemented
Snow Load
- not defined yet
Tests and Benchmarks
Static linear analysis
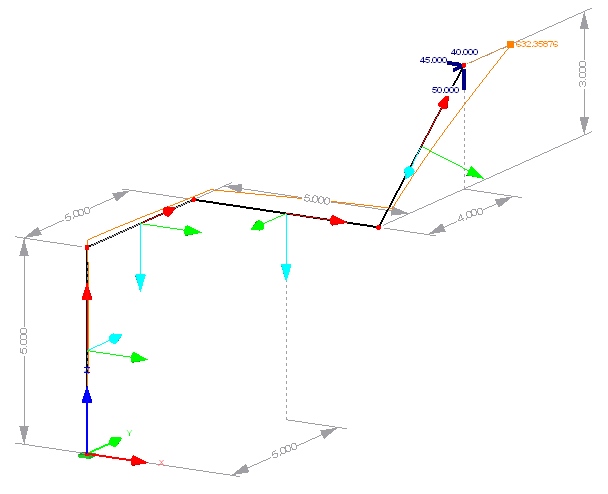
For the moment, the element BeamCR has successfully been tested in 3D in all its linear static features, including
- bending, axial deformation, torsion,
- shear deformation (separately definable for both local axes),
- rotation around the local axis.
As an example, the structure on the right was part of the final tests. The displacement of the end-point is (1.432, 0.336, 0.716), which leads to a total displacement of 1.636.
Static non-linear analysis
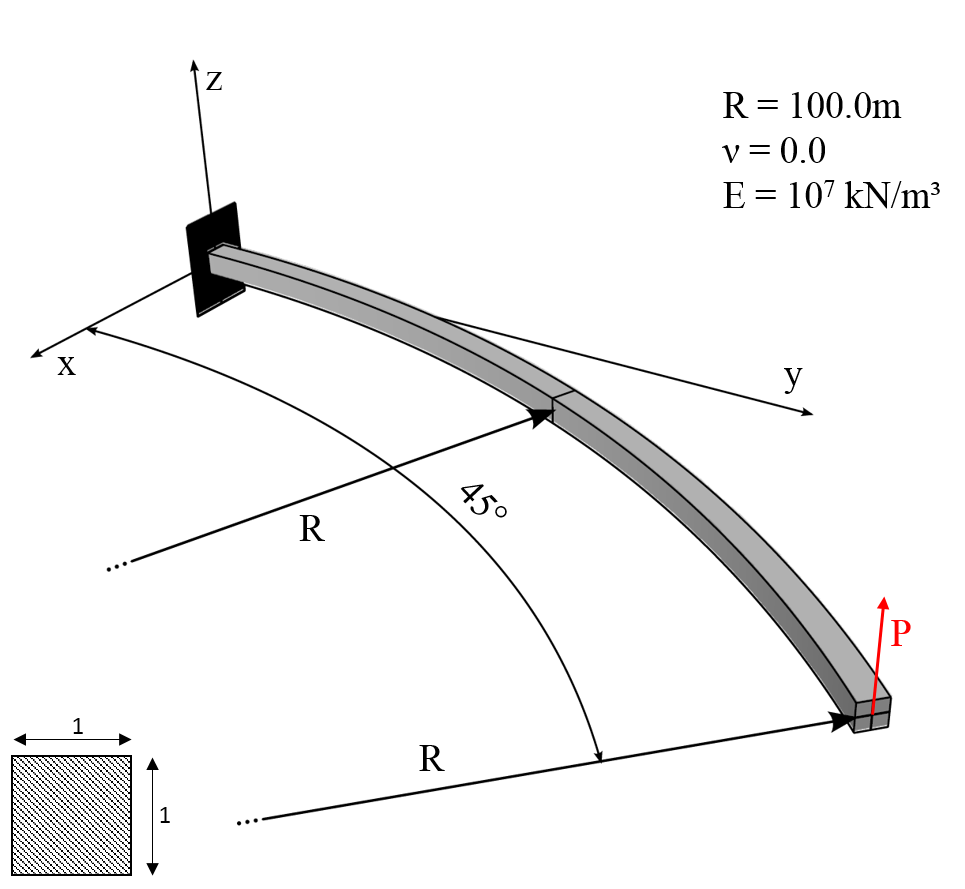
Test herefore is a large displacement response of a cantilever 45-degree bend subjected to a concentrated end load [1] p. 980 The structure is modeled by eight beam_CR-elements. One single load is applied at the free end of the cantilever. The non-dimensional tip deflection for P=7R²/EI=583.33 is w/R=0.53.
Theory
The element implementation mainly follows the implementation of a non-linear co-rotational 3D-beam element in Krenk [2].
As it is based on linear ansatz-functions, the BeamCR-element needs sufficiently fine discretization in order to converge to the true solution.
References
- ↑ Bathe, K.-J.: Large Displacement Analysis Of Three-Dimensional Beam Structures
- ↑ Krenk, S.: Non-linear Modeling and Analysis of Solids and Structures
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |