Users:General FEM Analysis/Materials Reference/Tsai-Wu Failure Criterion
From Carat++ Public Wiki
< Users:General FEM Analysis | Materials Reference(Difference between revisions)
| (3 intermediate revisions by one user not shown) | |||
| Line 2: | Line 2: | ||
== General Description == | == General Description == | ||
| − | + | Tsai-Wu Failure Criterion | |
| + | <ref> | ||
| + | S. W. Tsai and E. M. Wu. A General Theory of Strength for Anisotropic Materials. Journal of | ||
| + | Composite Materials, 5(1):58–80, January 1971. | ||
| + | </ref> | ||
| + | is a practically simple failure criterion which takes interaction of stresses in different directions into account by making use of strength tensors. It is considerably cheaper in computational effort compared to Puck criterion especially in 3D stress states. A drawback of this criterion is that it is based on von Mises criterion which is more suitable for ductile materials. 2D and 3D formulations are implemented into Carat++. As it can not distinguish between different fracture modes, Tsai-Wu Criterion returns one failure index for corresponding failure analysis. | ||
| + | |||
| + | |||
| + | == Tsai-Wu Fracture Condition Function == | ||
| + | |||
| + | |||
| + | [[File:Tsai-wu fracture condition function.png|350px]] | ||
| + | |||
== Tsai-Wu in 2D == | == Tsai-Wu in 2D == | ||
| Line 8: | Line 20: | ||
=== Strength Analysis === | === Strength Analysis === | ||
| − | Fracture envelope for a 2D failure analysis | + | Fracture envelope for a 2D failure analysis: |
<ref> | <ref> | ||
| − | + | Altug Emiroglu, Master Thesis: Comparative Study of Puck and Tsai-Wu Failure Criteria, Technische Universität München, 2013. | |
| − | + | ||
</ref> | </ref> | ||
| − | |||
[[File:tsai-wu_2D.png|400px]] | [[File:tsai-wu_2D.png|400px]] | ||
| Line 102: | Line 112: | ||
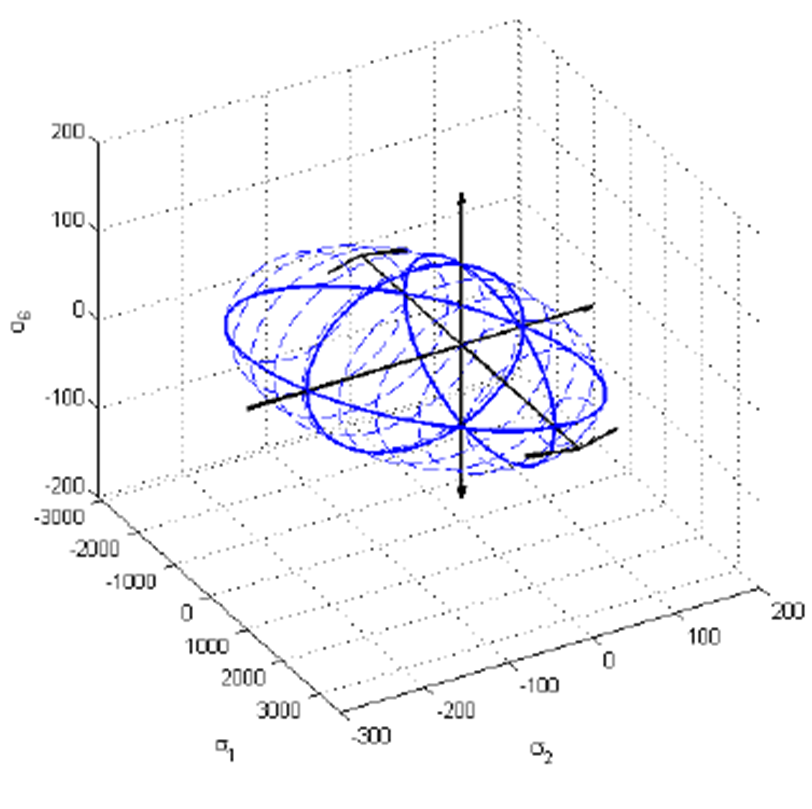
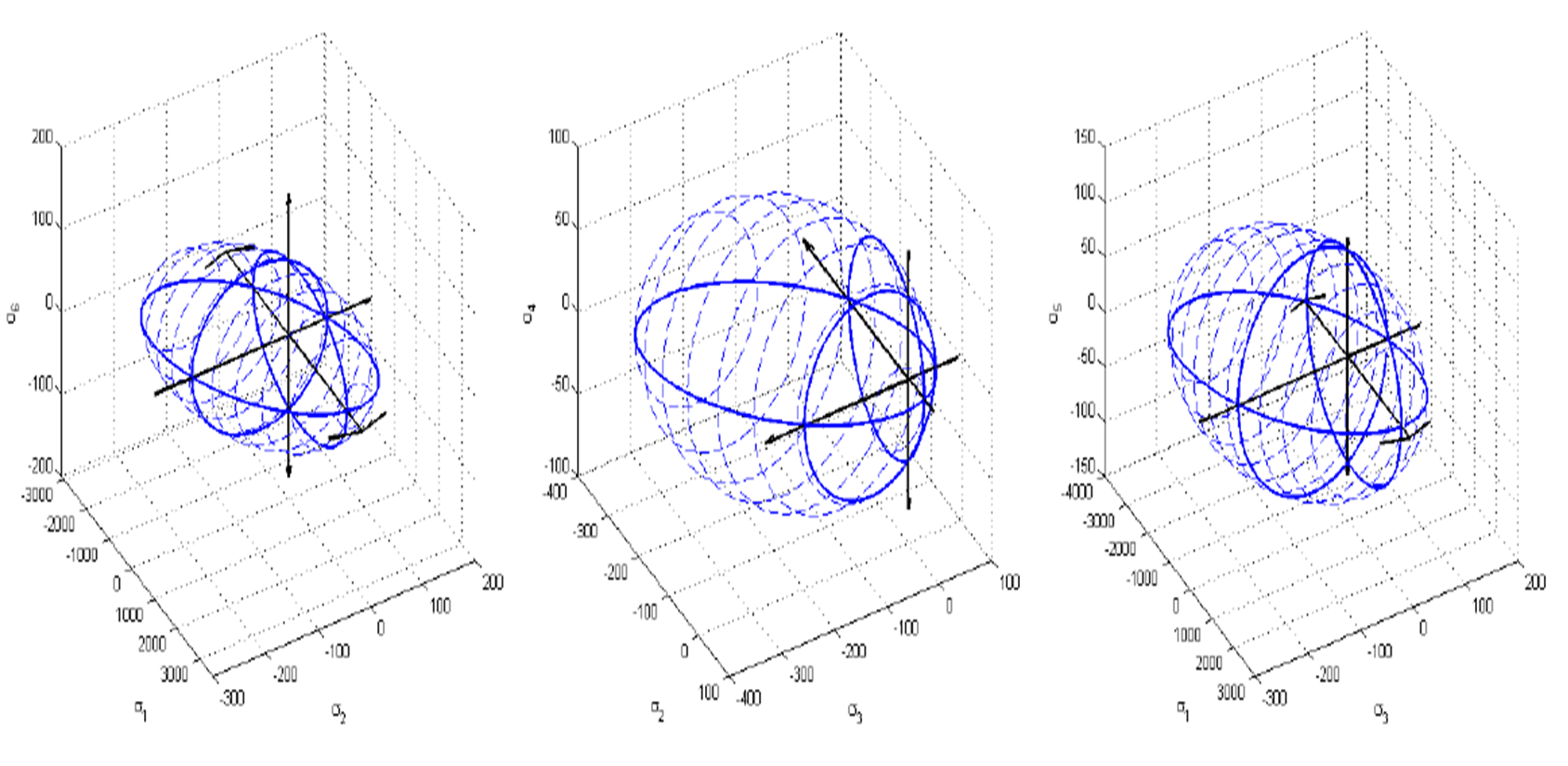
Fracture envelopes for a 3D failure analysis: | Fracture envelopes for a 3D failure analysis: | ||
| + | <ref> | ||
| + | Altug Emiroglu, Master Thesis: Comparative Study of Puck and Tsai-Wu Failure Criteria, Technische Universität München, 2013. | ||
| + | </ref> | ||
| − | [[File:tsai-wu_3D.png| | + | [[File:tsai-wu_3D.png|800px]] |
=== Parameter Description === | === Parameter Description === | ||
Latest revision as of 10:07, 15 February 2013
Contents |
General Description
Tsai-Wu Failure Criterion [1] is a practically simple failure criterion which takes interaction of stresses in different directions into account by making use of strength tensors. It is considerably cheaper in computational effort compared to Puck criterion especially in 3D stress states. A drawback of this criterion is that it is based on von Mises criterion which is more suitable for ductile materials. 2D and 3D formulations are implemented into Carat++. As it can not distinguish between different fracture modes, Tsai-Wu Criterion returns one failure index for corresponding failure analysis.
Tsai-Wu Fracture Condition Function
Tsai-Wu in 2D
Strength Analysis
Fracture envelope for a 2D failure analysis: [2]
Parameter Description
| Tsai-Wu Parameters (2D) | ||
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| T11 | real | Resistance to longitudinal tension (Direction 1) |
| C11 | real | Resistance to longitudinal compression (Direction 1) |
| T22 | real | Resistance to transverse tension (Direction 2) |
| C22 | real | Resistance to transverse compression (Direction 2) |
| S12 | real | Resistance to longitudinal shear |
| Optional Parameters | ||
| Parameter | Values, Default(*) | Description |
| STRESS TYPE | 2D, 3D | Indicates what kind of stress state should be used to calculate the failure condition. When not given, related element’s stress type is taken. |
| T33 | real | Resistance to tension in thickness direction (Direction 3) (De f ault = T22) |
| C33 | real | Resistance to compression in thickness direction (Direction 3) (De f ault = C22) |
| S13 | real | Resistance to longitudinal shear (De f ault = S 12) |
| FS12 | real | Coefficient, necessary for calculation of F12. (De f ault = -0.5) |
| F12 | real | F12 component of strength tensor; Fij. When not given, it is calculated using FS12. |
| P | real | Strength value, necessary for calculation of F12. See Section 3.2.3 |
| U | real | Strength value, necessary for calculation of F12. See Section 3.2.3 |
| V | real | Strength value, necessary for calculation of F12. See Section 3.2.3 |
Tsai-Wu in 3D
Strength Analysis
Fracture envelopes for a 3D failure analysis: [3]
Parameter Description
| Tsai-Wu Parameters (3D) | ||
| Compulsory Parameters | ||
| Parameter | Values, Default(*) | Description |
|---|---|---|
| T11 | real | Resistance to longitudinal tension (Direction 1) |
| C11 | real | Resistance to longitudinal compression (Direction 1) |
| T22 | real | Resistance to transverse tension (Direction 2) |
| C22 | real | Resistance to transverse compression (Direction 2) |
| S12 | real | Resistance to longitudinal shear |
| S23 | real | Resistance to transverse shear |
| Optional Parameters | ||
| Parameter | Values, Default(*) | Description |
| STRESS TYPE | 2D, 3D | Indicates what kind of stress state should be used to calculate the failure condition. When not given, related element’s stress type is taken. |
| T33 | real | Resistance to tension in thickness direction (Direction 3) (De f ault = T22) |
| C33 | real | Resistance to compression in thickness direction (Direction 3) (De f ault = C22) |
| S13 | real | Resistance to longitudinal shear (De f ault = S 12) |
| FS12 | real | Coefficient, necessary for calculation of F12. (De f ault = -0.5) |
| F12 | real | F12 component of strength tensor; Fij. When not given, it is calculated using FS12. |
| P | real | Strength value, necessary for calculation of F12. See Section 3.2.3 |
| U | real | Strength value, necessary for calculation of F12. See Section 3.2.3 |
| V | real | Strength value, necessary for calculation of F12. See Section 3.2.3 |
| FS13 | real | Coefficient, necessary for calculation of F13. (De f ault = -0.5) |
| F13 | real | F12 component of strength tensor; Fij. When not given, it is calculated using FS13. |
| FS23 | real | Coefficient, necessary for calculation of F23.(De f ault = -0.5) |
| F23 | real | F12 component of strength tensor; Fij. When not given, it is calculated using FS23. |
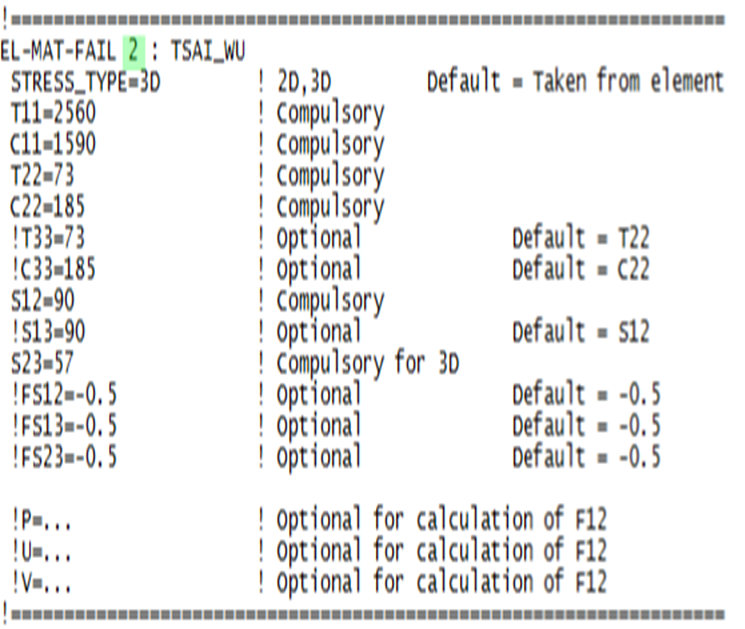
Example of a Complete Input Block
References
- ↑ S. W. Tsai and E. M. Wu. A General Theory of Strength for Anisotropic Materials. Journal of Composite Materials, 5(1):58–80, January 1971.
- ↑ Altug Emiroglu, Master Thesis: Comparative Study of Puck and Tsai-Wu Failure Criteria, Technische Universität München, 2013.
- ↑ Altug Emiroglu, Master Thesis: Comparative Study of Puck and Tsai-Wu Failure Criteria, Technische Universität München, 2013.
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |