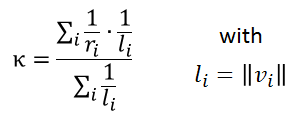Users:Structural Optimization/Response Functions/SurfaceCurvature

Revision as of 07:41, 26 April 2011 (view source) Helles (Talk | contribs) (→Input Parameters) ← Older edit		Revision as of 08:32, 26 April 2011 (view source) Helles (Talk | contribs) Newer edit →
Line 79:		Line 79:
	LAMBDA_ABS_MAX = 40		LAMBDA_ABS_MAX = 40
	</pre>		</pre>
		+
		+
		+	== A complete test example ==
		+
		+	=== Model description ===
		+	The considered test example is the optimization of a pinched cylinder applying a curvature limitation.
		+
		+	The following animation illustrates the eigenmodes of the plate.
		+	[[File:RespFunc_curvKS_system.jpg | center | 300px | pinched cylinder]]
		+
		+	=== Input File ===
		+	Here the full input file can be downloaded.
		+
		+	=== Documented Results ===
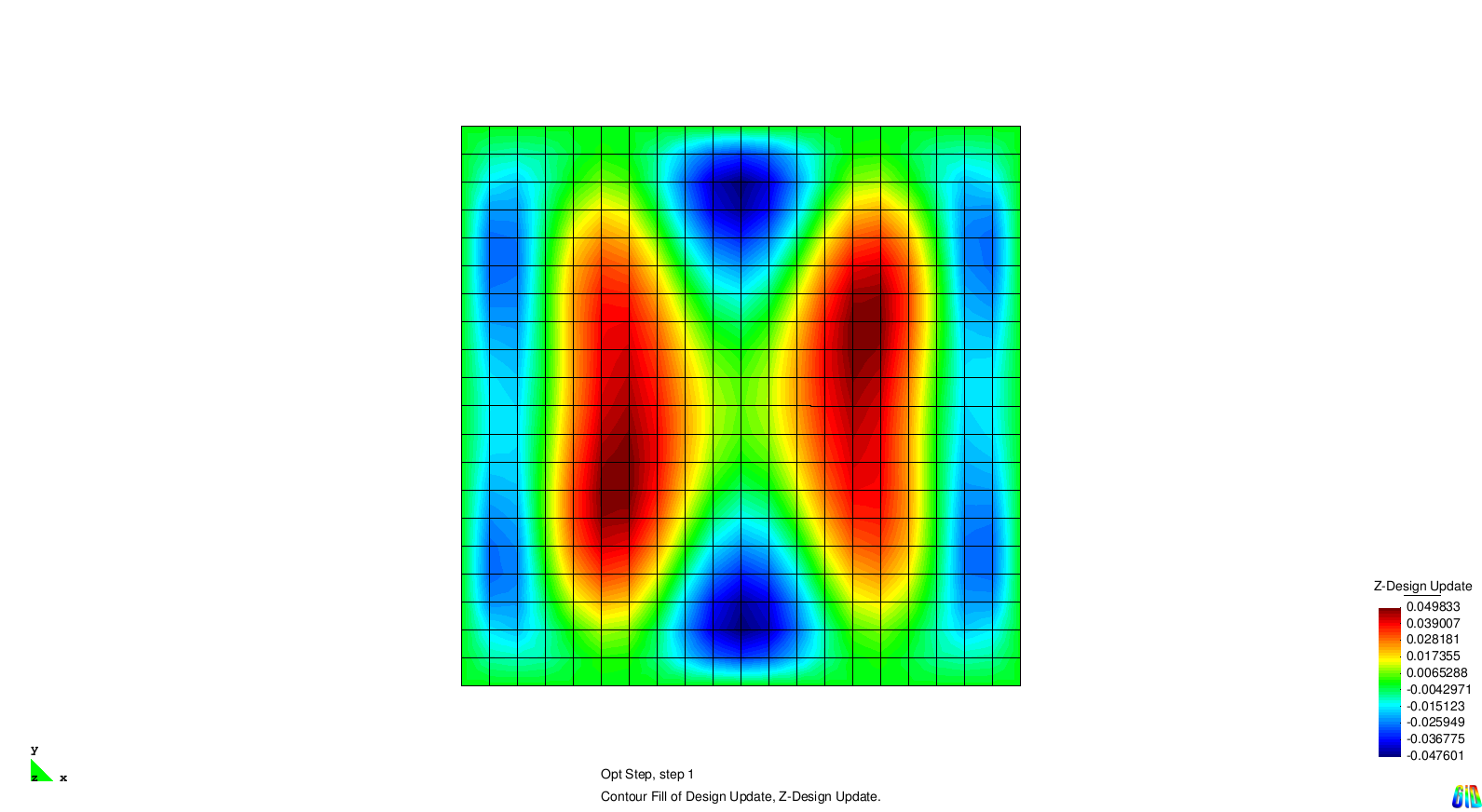
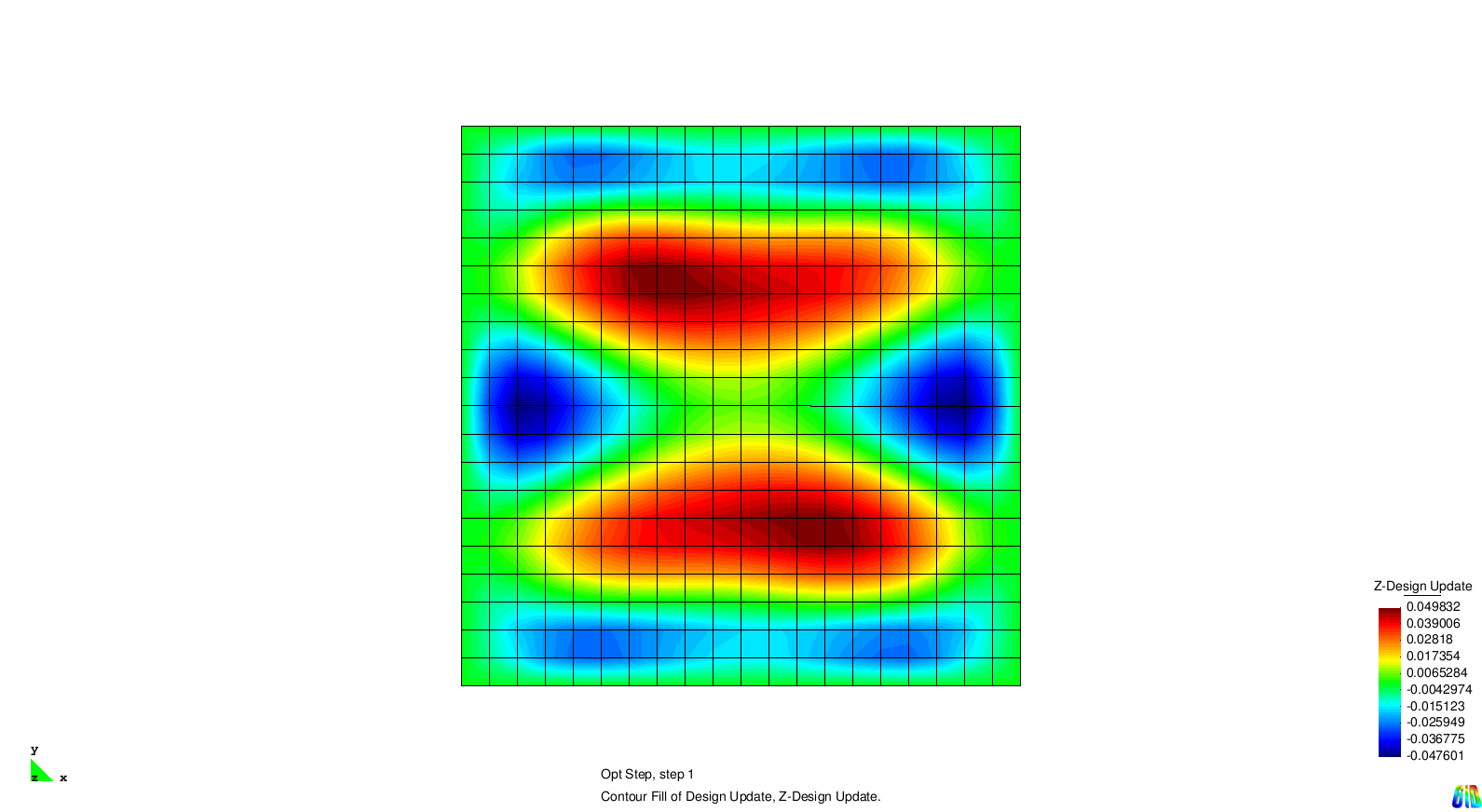
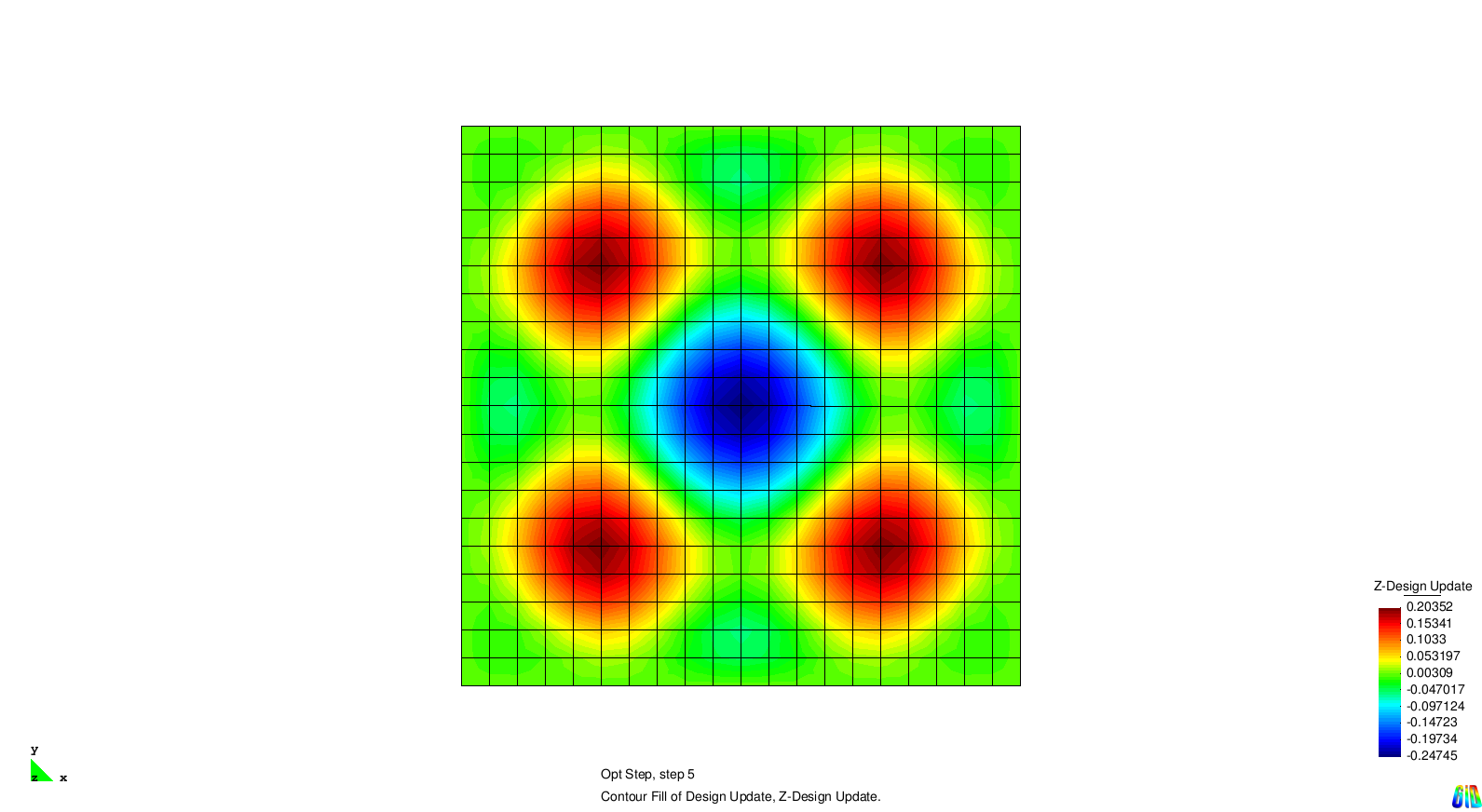
		+	The results show the expected behaviour. Each solution generates stiffness towards a certain eigenmode. As the modes two and three are symmetric it is not surprising that the design updates are symmetric, too.
		+
		+	<gallery caption="" widths="300px" heights="200px" perrow="2">
		+	File:RespFunc_eigenavalue_optdesign_1.PNG  |  Optimization result w.r.t. 1st eigenmode
		+	File:RespFunc_eigenavalue_optdesign_2.PNG  |  Optimization result w.r.t. 2nd eigenmode
		+	File:RespFunc_eigenavalue_optdesign_3.PNG  |  Optimization result w.r.t. 3rd eigenmode
		+	File:RespFunc_eigenavalue_optdesign_4.PNG  |  Optimization result w.r.t. 4th eigenmode
		+	</gallery>

---

Revision as of 08:32, 26 April 2011

Contents 1 General Description 1.1 Short Info 1.2 Estimation of nodal curvature 1.3 Kreisselmeier-Steinhauser weighting 2 Input Parameters 2.1 Example of a Complete Input Block 3 A complete test example 3.1 Model description 3.2 Input File 3.3 Documented Results

General Description

Short Info

In the field of structural optimization it is often necessary to apply a constraining of surface curvature in order to maintain manufacturing constraints. To this purpose, Carat++ provides an estimation tool to approximate the mean curvature at a surface node.

Estimation of nodal curvature

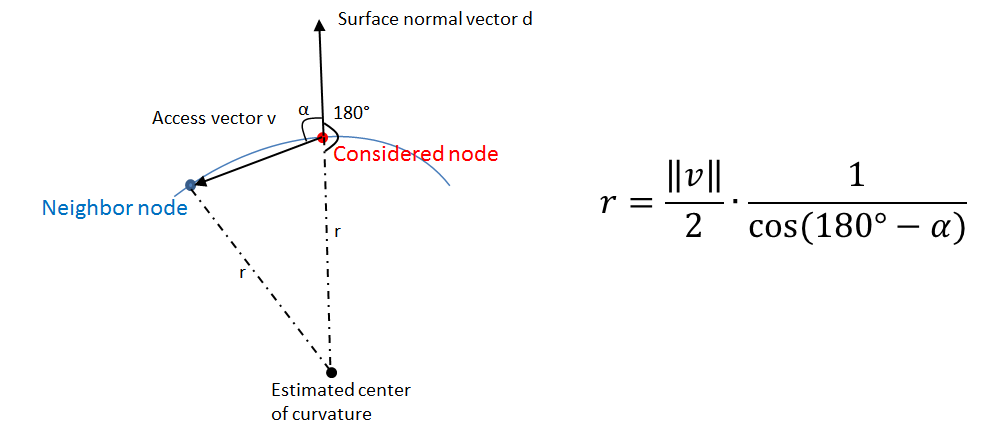
The nodal curvature is estimated using the surface normal vector and access vectors to the surrounding nodes. The estimation is based on a local spherical approximation of the geometry (see sketch below). So the radius of curvature r can be computed within the isosceles triangle.

Having computed this approximated radius of curvature for each surrounding node, the mean curvature of the surface is estimated by a weighted sum over all surrounding nodes i, whereat vi is the access vector to the ith node.

Kreisselmeier-Steinhauser weighting

Instead of constraining each single nodal curvature, Carat++ provides a technique to control the curvature within bigger element patches. To this purpose a Kreisselmeier-Steinhauser weighting is used.

Via the weighting parameter ρ the user can control to which extend exceedings of the maximum allowable curvature are weighted.

Input Parameters

Block headline
Parameter	Values, Default(*)	Description
OPT-RESPONSE_FCT	int : CURVATURE_PATCH_KS	Function ID and response function type.
Common compulsory parameters
ETA	real	Finite difference disturbance for sensitivity analysis
GRAD	DIRECT, ADJOINT	Method of gradient computation
SA	GLOBAL_FD, SEMI_ANALYTIC, EXACT_SEMI_ANALYTIC, ANALYTIC	Method of derivative computations inside sensitivity analysis
FDA	FOREWARD, CENTRAL, BACKWARD	Method of finite difference approximation (if neccessary for the chosen sensitivity analysis method)
DESVAR	OPT-VAR vector of integers	Design variables that are considered in the sensitivity analysis of this response function
Common optional parameters
WEIGHT	real, 1.0*	The weighting factor for this response function in multi-objective optimization
ANALYSIS	PC-ANALYSIS int	ID of the underlying analysis
Specific parameters
NODES	ND-SET int	Node set that includes all nodes this response function yields onto.
PATCH_SIZE	int	Size of patches (number of element rows) into which the NODES is sub-divided.
RHO	real	KS-weighting factor.
Common Compulsory Parameters for Constraints
Parameter	Values, Default(*)	Description
REL_LIMIT	real	Relative limit for constraint, depending on the actual value.
ABS_LIMIT	real	Absolute limit for constraint. Only one limit can be defined for a constraint.
CONSTRAINT_TYPE	INEQUALITY_LT, INEQUALITY_GT, EQUALITY	Type of constraint
Common Optional Parameters for Constraints
REL_TOLERANCE	real, 0*	Upper relative limit until which an inactive constraint is concidered as an active one
LAMBDA_ABS_MAX	real, 1/cepsilon*	Upper limit for lagrangian multiplier

Example of a Complete Input Block

OPT-RESPONSE_FCT 1 : CURVATURE_PATCH_KS
 WEIGHT=1.0
 ETA=1e-06
 GRAD=ADJOINT 
 SA= SEMI_ANALYTIC
 FDA=FOREWARD
 DESVAR=OPT-VAR 1
! -- specific parameters 
 NODES=ND-SET 1
 PATCH_SIZE = 5
 RHO = 15
! -- constraint parameters
 ABS_LIMIT = 0.25      ! KAPPA_MAX
 REL_TOLERANCE = 0.1
 CONSTRAINT_TYPE = INEQUALITY_LT
 LAMBDA_ABS_MAX = 40

A complete test example

Model description

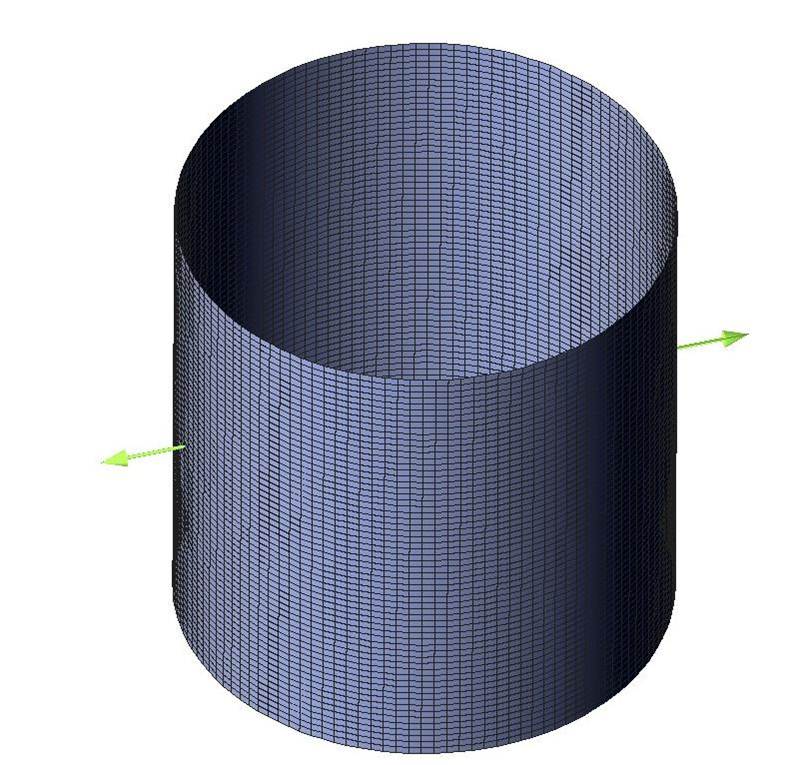
The considered test example is the optimization of a pinched cylinder applying a curvature limitation.

The following animation illustrates the eigenmodes of the plate.

Input File

Here the full input file can be downloaded.

Documented Results

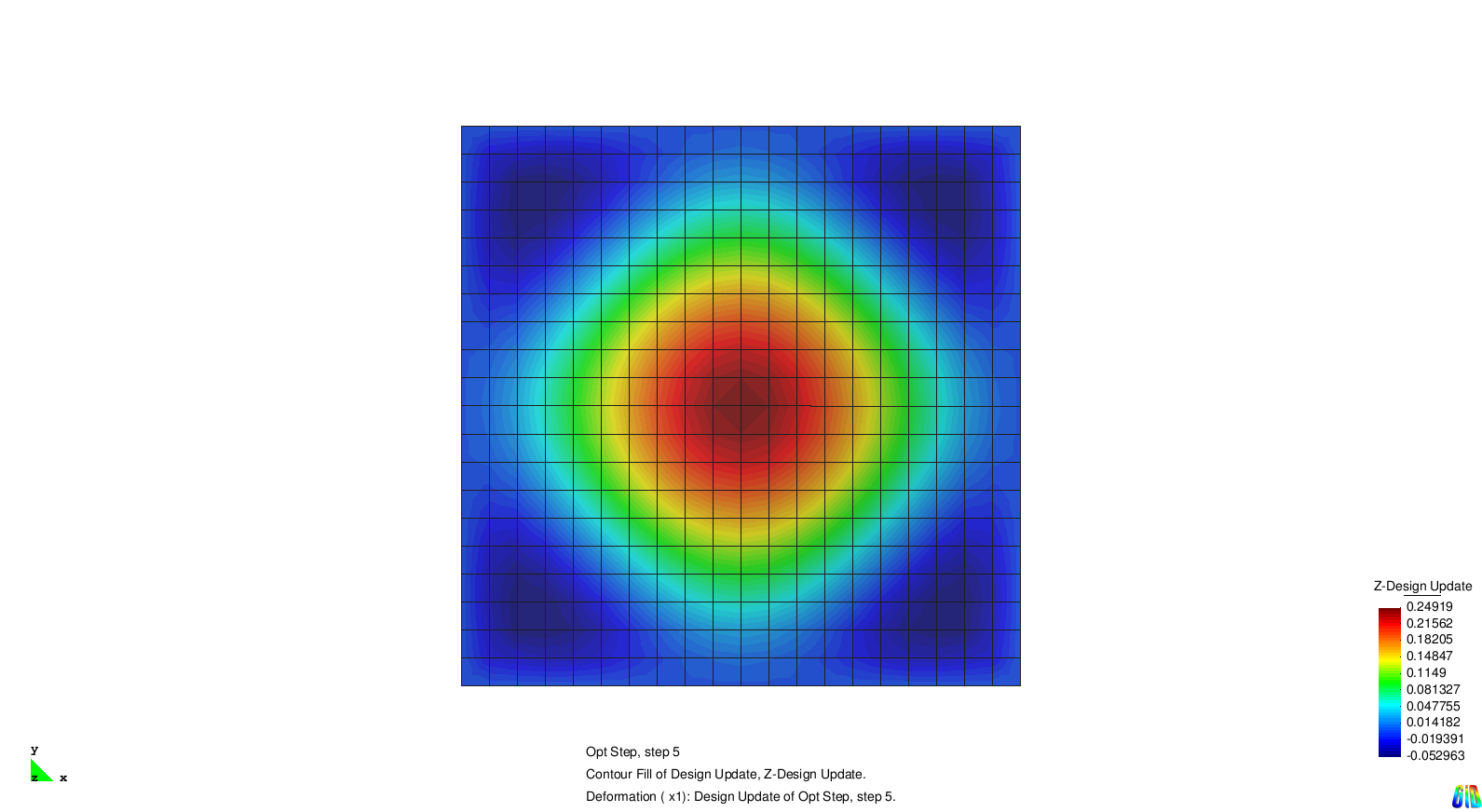
The results show the expected behaviour. Each solution generates stiffness towards a certain eigenmode. As the modes two and three are symmetric it is not surprising that the design updates are symmetric, too.

• 

  Optimization result w.r.t. 1st eigenmode

• 

  Optimization result w.r.t. 2nd eigenmode

• 

  Optimization result w.r.t. 3rd eigenmode

• 

  Optimization result w.r.t. 4th eigenmode

Whos here now:   Members 0   Guests 0   Bots & Crawlers 1