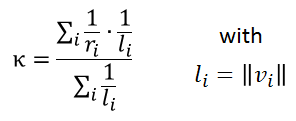Users:Structural Optimization/Response Functions/SurfaceCurvature
(→Estimation of nodal curvature) |
(→Estimation of nodal curvature) |
||
| Line 14: | Line 14: | ||
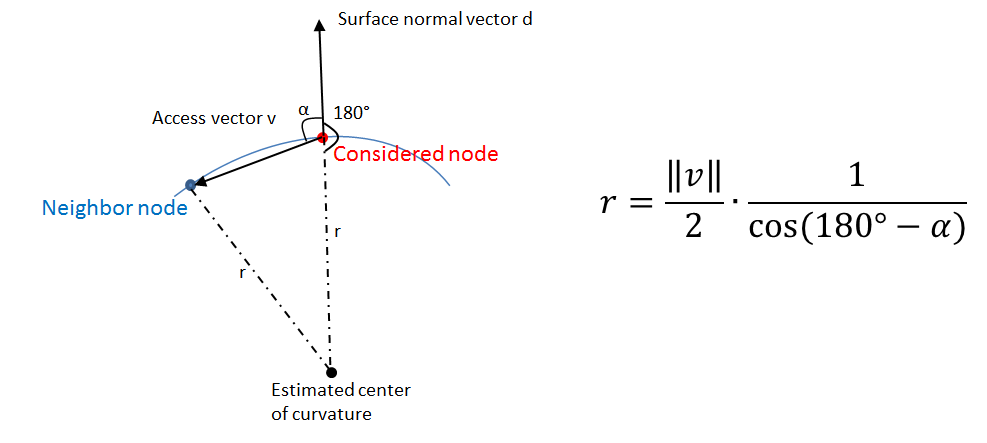
[[ File:curv_ks_sketch.png |500px | center |Sketch of curvature estimation in 1D ]] | [[ File:curv_ks_sketch.png |500px | center |Sketch of curvature estimation in 1D ]] | ||
| + | Having computed this approximated radius of curvature for each surrounding node, the mean curvature of the surface is estimated by a weighted sum over all surrounding nodes ''i'', whereat ''vi'' is the access vector to the ith node. | ||
[[ File:curv_ks_formula.png |300px | center | ]] | [[ File:curv_ks_formula.png |300px | center | ]] | ||
Revision as of 11:51, 21 April 2011
General Description
Short Info
In the field of structural optimization it is often necessary to apply a constraining of surface curvature in order to maintain manufacturing constraints. To this purpose, Carat++ provides an estimation tool to approximate the mean curvature at a surface node.
Estimation of nodal curvature
The nodal curvature is estimated using the surface normal vector and access vectors to the surrounding nodes. The estimation is based on a local spherical approximation of the geometry (see sketch below). So the radius of curvature r can be computed within the isosceles triangle.
Having computed this approximated radius of curvature for each surrounding node, the mean curvature of the surface is estimated by a weighted sum over all surrounding nodes i, whereat vi is the access vector to the ith node.
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |