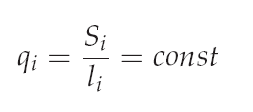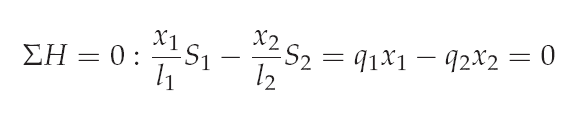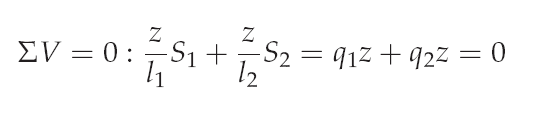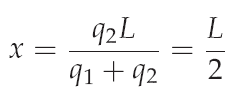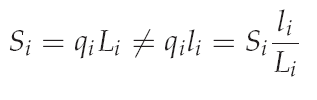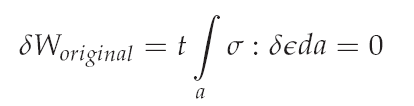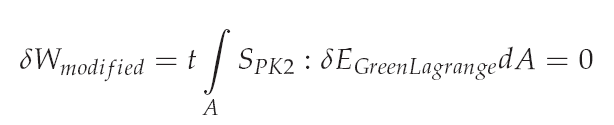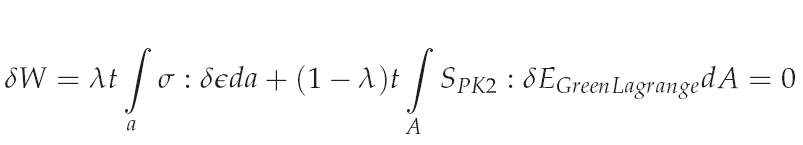Users:Form Finding/Numerical Methods for Form Finding
| Line 60: | Line 60: | ||
With the described modifications the principal of virtual work can be formulated in the refenrence configuration (see equation below): | With the described modifications the principal of virtual work can be formulated in the refenrence configuration (see equation below): | ||
| − | [[File:URS modified.PNG| | + | [[File:URS modified.PNG|400px|up|URS modified]] |
The equation above represents a modified but solvable Problem which is almost equal to the original problem in the converged situation of the ''URS'', when | The equation above represents a modified but solvable Problem which is almost equal to the original problem in the converged situation of the ''URS'', when | ||
| Line 66: | Line 66: | ||
To improve the convergence a homothopy method is used, which overlays the original problem with the modified one. To control the overlay a homotopy factor λ is used (see equation below). | To improve the convergence a homothopy method is used, which overlays the original problem with the modified one. To control the overlay a homotopy factor λ is used (see equation below). | ||
| − | [[File:URS complete.PNG| | + | [[File:URS complete.PNG|400px|up|URS complete]] |
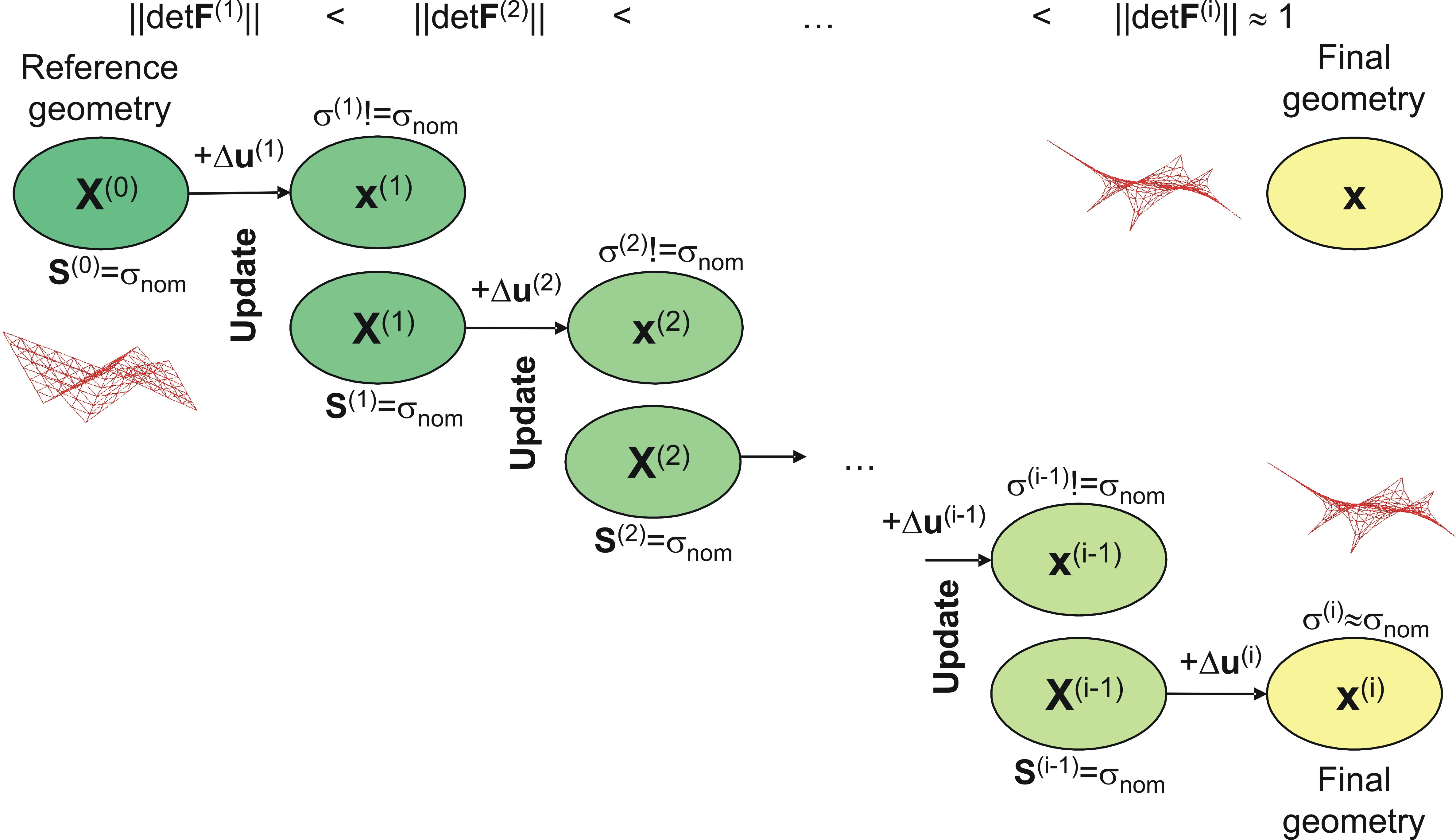
In figure below the principal process of ''{form finding'' with the ''URS'' is shown. The starting point of each calculation is the refernce geometry. These geometry is almost arbitray except the boundaries which have to be satisfied. W.r.t. this geometry the equilibrium equations presented above are solved with a Finite Element formulation. Herein the described modifications are used to get a solveable problem. After solving the system of equations the actual stress state σ<sup>i</sup> are compared with the final stress state σ<sup>nom</sup>. If the stresses are the same the procedure is converged. Normally more than on iteration step is needed for are converged solution. For the next iteration step the deformed geometry is used as the new reference configuration and the problem is solved again. In the final end the stress state should be almost identical. | In figure below the principal process of ''{form finding'' with the ''URS'' is shown. The starting point of each calculation is the refernce geometry. These geometry is almost arbitray except the boundaries which have to be satisfied. W.r.t. this geometry the equilibrium equations presented above are solved with a Finite Element formulation. Herein the described modifications are used to get a solveable problem. After solving the system of equations the actual stress state σ<sup>i</sup> are compared with the final stress state σ<sup>nom</sup>. If the stresses are the same the procedure is converged. Normally more than on iteration step is needed for are converged solution. For the next iteration step the deformed geometry is used as the new reference configuration and the problem is solved again. In the final end the stress state should be almost identical. | ||
| − | [[File:URS Process.jpg| | + | [[File:URS Process.jpg|600px|up|URS Process.jpg]] |
It can be seen that the ''URS'' is a general method which prevent the singular problem by doing a manipulation of the continuum mechanics. Due to that the method is | It can be seen that the ''URS'' is a general method which prevent the singular problem by doing a manipulation of the continuum mechanics. Due to that the method is | ||
entirely general and is applicable for all kind of strutural elements. | entirely general and is applicable for all kind of strutural elements. | ||
Due to the generallity and the continuum mechanical basis of the ''URS'' it is absolutly simple to integrate this method in a common Finite Element program. A describtion how to use the ''URS'' in CARAT++ can be found in section ''form finding with carat++''. | Due to the generallity and the continuum mechanical basis of the ''URS'' it is absolutly simple to integrate this method in a common Finite Element program. A describtion how to use the ''URS'' in CARAT++ can be found in section ''form finding with carat++''. | ||
Revision as of 16:00, 2 September 2010
Introduction
In the latter section we saw that the equations for a form finding problem are not unique and due to that fact we get a singular system of equations. To prevent this problem several methods are devoloped in the past. The most common ones are the force densitiy method and dynamic relexation. The force density method was developed in the context of designing cable net structures (e.g. olympic roof in munich). This method prevent the singularities by defining the force densities in the equation system. The dynamic relaxation modifiy the form finding problem into a dynamic problem. It can be understood as stabilize the form finding problem by adding mass and damping to the problem. A third method which which is able to solve the singular problem of form finding is the Updated Reference Strategy (URS) which was introduced by Univ.-Prof. Dr.-Ing. Kai-Uw Bletzinger in 1999. In the paper "A general finite element approach to the form finding of tensile structures by the updated reference strategy" he present a method which based on a full continuum mechanical description of the form finding problem. The main advandage of method is their generell applicability for all kind of structures. In the next sections the principles of the force densitiy method and the Updated Reference Strategy is discussed on the basis of the simple 2 bar truss example from the latter section.
Solving the 2 bar truss example with the force density method
To prevent the singular system of equations for the form finding the force density method was introduced. In these method the force densities are the ration of the cable force Si and the cable length Li. So the force density is definte as:
A main assumption of the force densitiy method is that the force densities are constant througth the form finding process. With the definition of equation of the force densities the horizontal and vertical equilibrium is written like:
The solution of the above equations gives again that z has to be zero (z=0) but know a certain solution for x can be evaluated (see equation below).
On the first glance it seems that the force density method gives a satisfactory solution of the form finding problem. But if we look more detailed on the solution some problem occurs, which should be discussed. In order to solve the form finding problem with the force density method an initial value for the length of the cables have to be chossen. In the following we interpret these initial length as the reference length Li. Due to solving the system of equations a change of the reference length occurs, due to evaluating the positon of node K. In this deformed configuration the length of the certain cables diverse from the reference length. This new length represents the actual length li. Due to the assumption, that the force densities are constant over the whole form finding process the cable forces w.r.t. the actual states diveres from the initial cable forces.
The fact from above equation can be interpreted like the following. From the force density method we get a solution which is an approximation of the final configuration which allows variations in the stress state from the choosen stress state. It should be noticed that the solution of the force density method is a surface in self equilibrium w.r.t. the actual stress state, but has meaningful diverences to the final stress state. In order to get a solution that satisfy not only equilibrium but also the final stress state the Updated Reference Strategy was introduced.
Solving the 2 bar truss example with the updated reference strategy
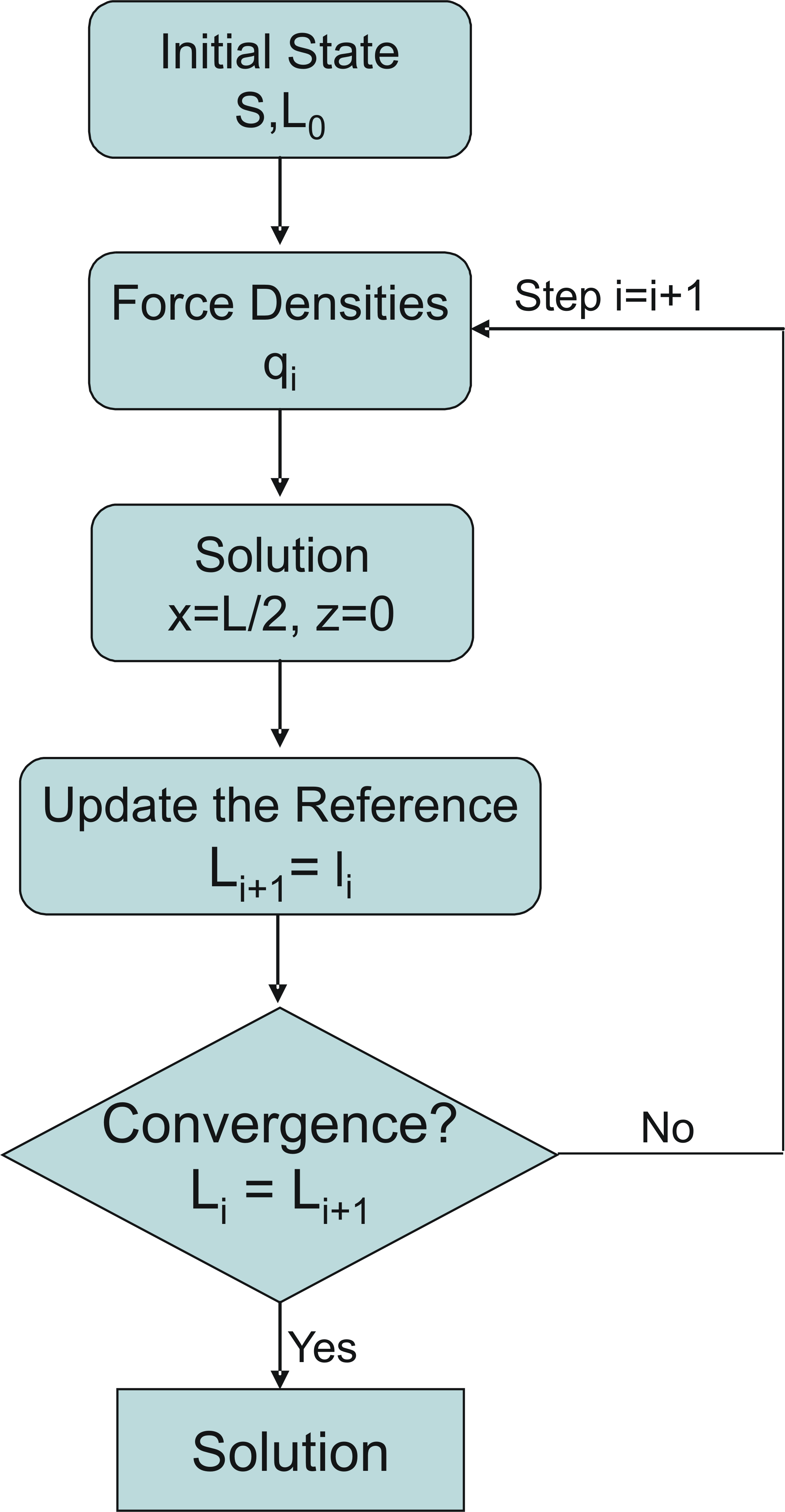
The main disadvantage of the force density method is the assumption of constant force densities and the non matching stress states at the end of the form finding process. The Updated Reference Strategy (URS) tries to prevent exactly these disadvantages. The main idea of URS is to repeat the solution of the problem put change the problem in that way, that at the end also the equilibrium and the stress state is satisfied. To do so, the URS uses the actual cable length li as the new reference length Li+1 for the next iteration step in an iterative solution process of the problem. The Figure below illustrate the process.
The main advantage of this method is that in the final end the equilibrium is satisfied and also the choosen stress state. For the example of the 2 bat truss the URS converges in the second itartaion step to the final solution. For more comlexe examples there are more iteration steps necessary to find the final solution. If we have a more abstract look on the URS we see that in contrast to the force density method not the force densities are constant through the form finding but the stress state. This fact opend the way to a general formulation of the form finding problem in a continuum mechanical way. In contrast to the force densities, which are only available for cables, the stresses are quantities which all kind of elements are dealing with. With the stresses as the constant values it is possible to formulate the original singular problem with the principal of virtual work (see equation below).
Were σ is the choosen prestress state (Chauchy stresses), a is the surface area in the actual configuration, t is the membrane thickness and ε are the strains (Euler-Almansi strains). To get a solvable system of equation a few modifications of the singular original problem have to be done.
- Start from an abritray reference configuration that satisfy the boundary condition - Interpret the Chauchy stresses $\sigma$ as Piola-Kirchhoff stresses of second kind SPK2 -> true for actual configuration = reference configuration li=Li
With the described modifications the principal of virtual work can be formulated in the refenrence configuration (see equation below):
The equation above represents a modified but solvable Problem which is almost equal to the original problem in the converged situation of the URS, when the reference configuration X and the actual configuration x are identical. To improve the convergence a homothopy method is used, which overlays the original problem with the modified one. To control the overlay a homotopy factor λ is used (see equation below).
In figure below the principal process of {form finding with the URS is shown. The starting point of each calculation is the refernce geometry. These geometry is almost arbitray except the boundaries which have to be satisfied. W.r.t. this geometry the equilibrium equations presented above are solved with a Finite Element formulation. Herein the described modifications are used to get a solveable problem. After solving the system of equations the actual stress state σi are compared with the final stress state σnom. If the stresses are the same the procedure is converged. Normally more than on iteration step is needed for are converged solution. For the next iteration step the deformed geometry is used as the new reference configuration and the problem is solved again. In the final end the stress state should be almost identical.
It can be seen that the URS is a general method which prevent the singular problem by doing a manipulation of the continuum mechanics. Due to that the method is entirely general and is applicable for all kind of strutural elements. Due to the generallity and the continuum mechanical basis of the URS it is absolutly simple to integrate this method in a common Finite Element program. A describtion how to use the URS in CARAT++ can be found in section form finding with carat++.
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |