Users:General FEM Analysis/BCs Reference/Neumann
(→PRES) |
|||
| Line 20: | Line 20: | ||
Pressure is an element load acting on an element '''surface'''. It is usually acting normal to the element surface, so defining a direction is not necessary. If a different acting direction is desired it can be defined via the direction vector '''in local element coordinates'''. The load value is equal to the value entered in the load definition. | Pressure is an element load acting on an element '''surface'''. It is usually acting normal to the element surface, so defining a direction is not necessary. If a different acting direction is desired it can be defined via the direction vector '''in local element coordinates'''. The load value is equal to the value entered in the load definition. | ||
| − | + | ||
| − | + | <pre> | |
LD-ELEM 1 PART=1 | LD-ELEM 1 PART=1 | ||
LD-CURVE = LD-CURVE 1 | LD-CURVE = LD-CURVE 1 | ||
| Line 30: | Line 30: | ||
</pre> | </pre> | ||
| + | {| | ||
| [[File:BCs_loads_pressure.PNG | 400px | outline pressure load]] | | [[File:BCs_loads_pressure.PNG | 400px | outline pressure load]] | ||
|} | |} | ||
Revision as of 08:58, 2 September 2010
Some general remarks concerning Neumann conditions:
- The parameter LD-CURVE is an optional input. It is only used in dynamic analyses. For non-linear statics the load curve has to be defined in the analysis block.
Contents |
Node Loads (LD-NODE)
A node load is the most simple kind of Neumann boundary condition. A force or a bending moment is directly applied to a finite element node, whereat the load is defined by its direction and its value. The length of the direction defining vector [D1, D2, D3] does not play any role.
LD-NODE 1 TYPE = FORCE LD-CURVE = LD-CURVE 1 NODE 1 D1 = 1.0 D2 = 0.0 D3 = 0.0 VAL = 10 NODE 2 D1 = 0.0 D2 = 0.0 D3 = 1.0 VAL = 20
Element Loads (LD-ELEM)
A more complex way of defining Dirichlet conditions is to apply a constraint not to a node but to an element, so the element itsself has to determine its equivalent nodal forces. Depending on the direction and the influenced area one can distinguish between snow load, dead load and pressure load.
PRES
Pressure is an element load acting on an element surface. It is usually acting normal to the element surface, so defining a direction is not necessary. If a different acting direction is desired it can be defined via the direction vector in local element coordinates. The load value is equal to the value entered in the load definition.
LD-ELEM 1 PART=1 LD-CURVE = LD-CURVE 1 TYPE=PRES VAL=10 ! input using default direction D1=0 D2=0 D3=1 ! alternative input for pressure parallel to the element surface acting parallel to the element's 1st local coordinate TYPE=PRES D1=1.0 D2=0.0 D3=0.0 VAL=10
|
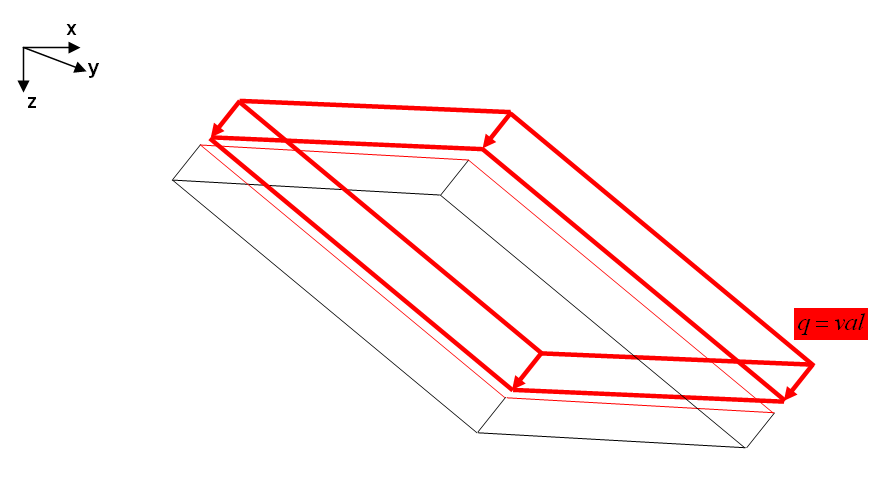
SNOW
Snow load is also an element surface related load. In contrast to pressure load it is defined by a direction and it is not acting onto the complete element surface but on its projection into the plane normal to the direction of action. The picture below shows snow load acting into z-direction onto an inclined element.
LD-ELEM 1 PART=1 LD-CURVE = LD-CURVE 1 TYPE=SNOW D1 = 0.0 D2 = 0.0 D3 = 1.0 VAL=10 |
|
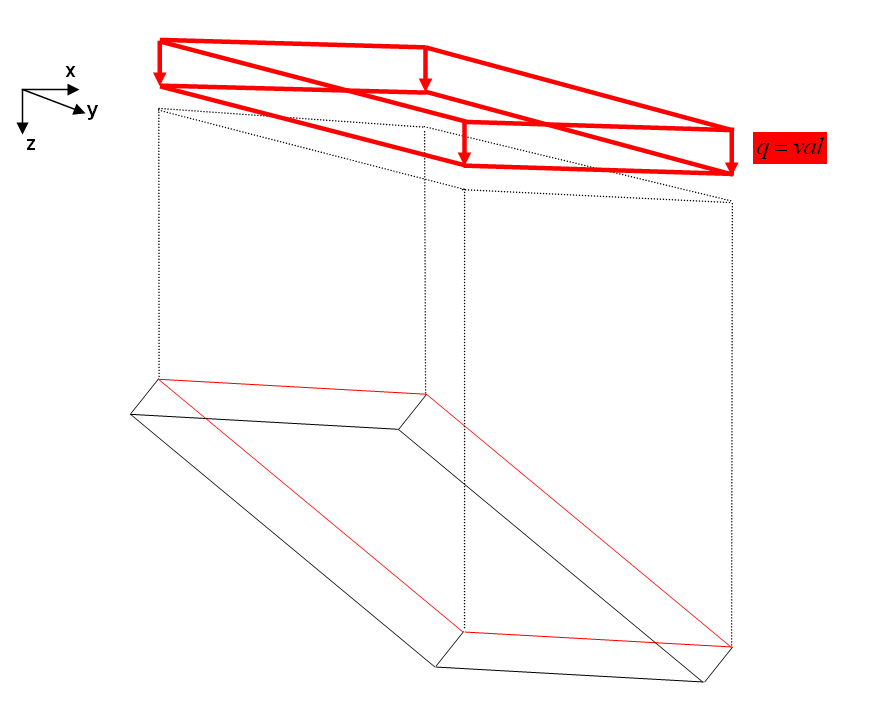
DEAD
Dead load is acting onto the whole volume of an element. It is computed by multiplying material's density times the load value, which should be equal to gravity's acceleration. Gravity's direction can be defined by the direction vector [D1, D2, D3]. The following input block represents material and load parameters for concrete material and gravity acting in z-direction.
EL-MAT 1 : LIN_ELAST_ISOTROPIC EMOD=3.5e10 ALPHAT=1e-5 DENS=2.5e3 NUE=0.2 LD-ELEM 1 PART=1 LD-CURVE = LD-CURVE 1 TYPE=DEAD D1=0.0 D2=0.0 D3=1.0 VAL=9.81 |
|
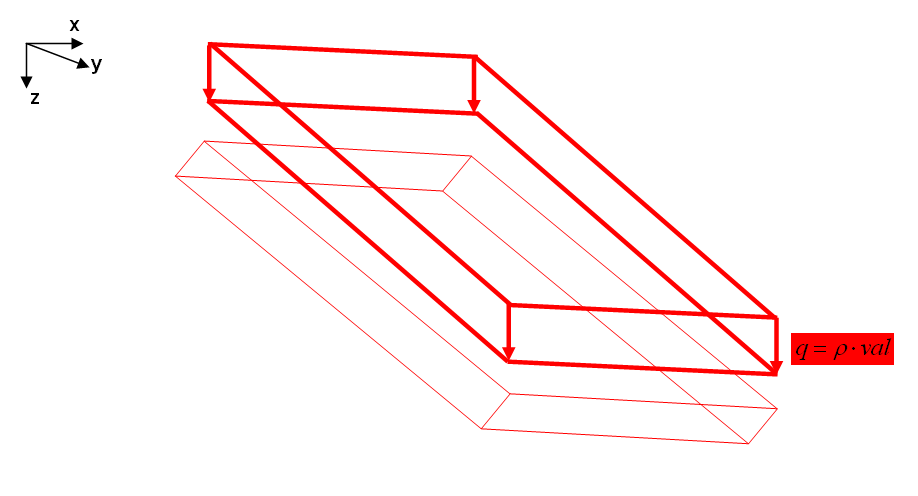
TEMPERATURE
(This part is currently under development. Author: Helmut. Date: 08/2010.)
The second kind of volume load is the temperature load object. In contrast to the loads mentioned above it is not defined by elements but by nodes, as the underlying temperature field is defined by nodal values. To this purpose it is possible to define multiple temperature layers at one node, for example top and bottom layer of a shell.
As an example we consider a U-shaped cantilever, where we describe a temperature of +10 over reference temperature at the lower edge and -10 below reference temperature at the top edge.
LD-ELEM 1 TYPE = TEMPERATURE INTERPOLATE_PART = 1 ND-SET = 30 LAYER = 1 VAL = 10 ND-SET = 23 LAYER = 1 VAL = -10 |
|
Although we only prescribed the temprature at the upper and lower edge we receive a temperature filed which is linear over the height. This is due to the fact that we inputed INTERPOLATE_PART = 1 which forces to interpolate the temperature field for all nodes belomging to part 1. If one omited this input flag all nodes offside the defined edges would be assigned reference temperature and so the displacement would differ significantly.
temperature field after inperpolation was applied
resulting displacement
temperature field without inperpolation
resulting displacement
Load curve
A load curve is used to define time depending load factors for non-linear static analysis or dynamics.
The concept is quite simple: The user specifies a discrete load factor-time-function and values in between are interpolated linearly.
LD-CURVE 1 TYPE=DISCRETE TIME = 0.000 VAL = 0.0000 TIME = 1.000 VAL = 1.0000 TIME = 10.000 VAL = 2.0000 TIME = 12.000 VAL = 0.0000 |
Hints:
|
| Whos here now: Members 0 Guests 0 Bots & Crawlers 1 |
