Users:General FEM Analysis/Elements Reference/Beam1

From Carat++ Public Wiki
< Users:General FEM Analysis | Elements Reference(Difference between revisions)
Jump to: navigation, search
(→General Description)
 
(58 intermediate revisions by one user not shown)
Line 1: Line 1:
−
Coded, still under development and testing.
 
−
Missing:
 
−
* documentation in Carat++-Wiki
 
−
* benchmark-examples
 
−
 
−
Coming soon
 
−
 
−
 
 
[[Category: Users:General FEM]]
 
[[Category: Users:General FEM]]
  
Line 13: Line 5:
 
=== Element Type ===
 
=== Element Type ===
  
−
* This beam element is a linear 3D-beam taking into account shear deformation (Timoshenko-beam element).
+
* This beam element is a 2 node linear 3D-beam taking into account shear deformation (Timoshenko-beam element). For non-linear analyses the element is enriched by theory of 2nd order kinematics.
−
* This beam element has 6 DOFs per node (three translations and three rotations)
+
* This beam element has 6 DOFs per node (three translations and three rotations).
 +
* The stiffness matrix for the linear calculation is hard-coded, thus not needing any integration. For theory of 2nd order, the normal force in the element leads to modifications in the stiffness matrix.
  
 
=== Degrees of Freedom ===
 
=== Degrees of Freedom ===
Line 20: Line 13:
 
For the Beam1 element use the 3 translatoric degrees of freedom ''DISP_X, DISP_Y, DISP_Z'' and the 3 rotatoric degrees of freedom ''ROT_X, ROT_Y, ROT_Z''.
 
For the Beam1 element use the 3 translatoric degrees of freedom ''DISP_X, DISP_Y, DISP_Z'' and the 3 rotatoric degrees of freedom ''ROT_X, ROT_Y, ROT_Z''.
  
 +
=== Theory of 2nd Order ===
 +
 +
If Theory of 2nd Order should be taken into account, a nonlinear calculation (ANALYSIS STA_GEO_NLIN) with only one timestep has to be executed. The stiffness matrix is calculated with the accurate auxiliary values (“Strichwerte”) A’, B’ and D’ see <ref name="Statik  Ergänzung - Skript"> Bletzinger, K.-U.: Statik  Ergänzung - Skript </ref>. In case of nonlinear calculation the shear correction factors are no longer considered.
 +
 +
=== Dynamic ===
 +
 +
Since a mass-matrix is implemented, the Beam1-element can also be used in dynamic analyses (including eigenfrequency,...) where it has already been successfully applied.
 +
 +
=== Orientation of the local coordinate system ===
 +
 +
The Beam1 element uses the following definition for the determination of the local coordinate system (needed for the orientation of IYY and IZZ,...):
 +
* the local x-axis is oriented from node 1 to node 2 of the beam
 +
* the local y-axis lies in the global XY-plane, such that the local z-axis points in the same half-space as the global Z-axis (mathematically spoken: the local z-axis and the global Z-axis result in a positive dot-product)
 +
* the local z-axis is perpendicular to the other two local axis, following the right-hand-rule for x-y-z
 +
* '''exception:''' If the local x-axis (i.e. the beam axis) points in the direction of global Z, the local y-axis points in the direction of the global Y-axis. The local z-axis once again follows the right-hand-rule for x-y-z.
 +
 +
In case that a rotation of the local coordinate system is needed (rotated elements, inverse definition of IYY and IZZ,...) an angle ''THETA'' has to be specified. This angle rotates the whole coordinate system around the local x-axis, following the right-thumb rule (i.e. the thumb of the right hand points in the direction of the local x-axis).
 +
 +
=== Orientation of the resultant forces ===
 +
 +
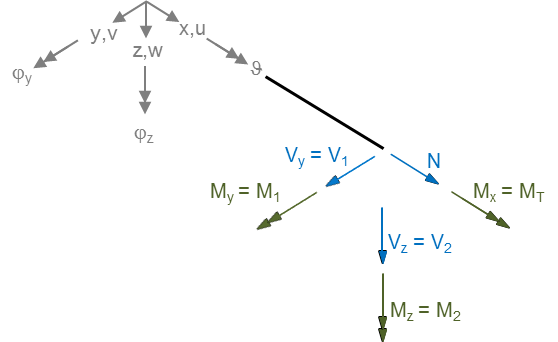
The Beam1 element has 6 resultant forces in accordance with the degrees of freedom. The resultant forces, ''[ N V1 V2 | MT M1 M2 ]'', are oriented along the local axes on the positive section of the beam. Note that the resultant forces are evaluated in the center of the beam element, so it's the mean value of the two ends. For the orientation, cf. also the orientation sketch:
 +
[[File:Beam1-Resultant_forces_orientation.png|200px|frame|right|Resultant forces orientation for element Beam1]]
  
 
== Input Parameters ==
 
== Input Parameters ==
Line 41: Line 56:
 
|Definition of the cross-sectional area of the beam
 
|Definition of the cross-sectional area of the beam
 
|-
 
|-
−
!I_YY, I_ZZ
+
!IYY, IZZ
 
|
 
|
 
|Definition of the moments of inertia
 
|Definition of the moments of inertia
−
|-
 
 
|-
 
|-
 
|colspan="3" style="background:#efefef;"| Optional Parameters
 
|colspan="3" style="background:#efefef;"| Optional Parameters
 +
|-
 +
!KY, KZ
 +
|0
 +
|Shear correction factor; if 0 or no value specified, shear is not taken into account (Bernouolli-beam theory); <br> '''Note:''' For Theory of 2nd Order, Bernoulli-beam theory is assumed.
 +
|-
 +
!THETA
 +
|0
 +
|Angle of rotation of the local coordinate system around the beam axis in degrees
 +
|-
 
|}
 
|}
  
Line 55: Line 78:
 
AREA=5.555  IYY=1.222  IZZ=1.333
 
AREA=5.555  IYY=1.222  IZZ=1.333
 
KY=1.4  KZ=1.5
 
KY=1.4  KZ=1.5
 +
THETA=90
 
</pre>
 
</pre>
  
 +
=== Use of the shear correction factors KY and KZ ===
 +
The shear correction factors ''KY'' and ''KZ'' depend on the cross section of the beam. For a rectangle, ''KY'' resp. ''KZ'' are usually considered equal to 1.2, which gives a factor of α=1/''Ki''=5/6.
  
−
== Element Loading ==
+
=== Use of the rotation parameter THETA ===
 +
The rotation parameter ''THETA'' and its use is explained in the section concerning the coordinate system above.
  
−
=== Pressure ===
+
=== The torsional resistance IT ===
−
* not defined yet
+
The torsional resistance ''IT'' is interpreted as the polar moment ''Ipp'', i.e.: ''IT'' = ''Ipp'' = ''IYY'' + ''IZZ''.
 +
 
 +
== Element Loading ==
 +
For the moment, only nodal forces in the three global directions can be applied (i.e. ''Fx, Fy, Fz'').
 +
Being a line element not all general load cases are applicable.
  
 
=== Dead Load ===
 
=== Dead Load ===
−
* not defined yet
+
* implemented
  
−
=== Snow Load ===
+
== Tests and Benchmarks ==
−
* not defined yet
+
=== Static linear analysis ===
 +
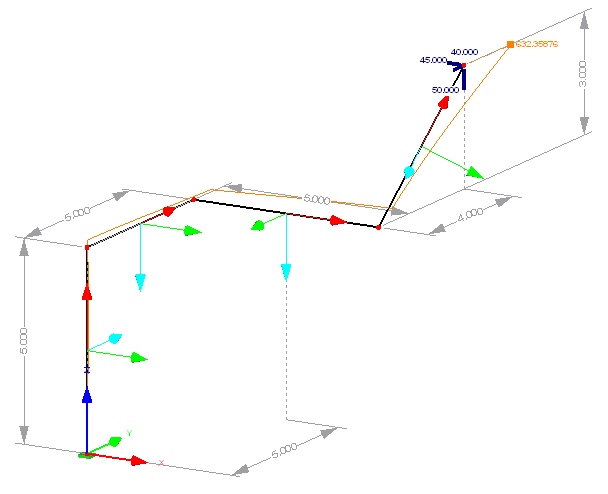
[[File:linBeamTests2.jpg|400px|frame|right|Static test for element Beam1]]
 +
For the moment, the element Beam1 has successfully been tested in 3D in all its linear static features, including
 +
* bending, axial deformation, torsion,
 +
* shear deformation (separately definable for both local axes),
 +
* rotation around the local axis.
  
 +
As an example, the structure on the right was part of the final tests.
  
 +
=== Theory of 2nd order ===
 +
Test herefore is a clamped frame with one pillar under compression and the other under tension cp. "Statik  Ergänzung - Skript" <ref name="Statik  Ergänzung - Skript"> Bletzinger, K.-U.: Statik  Ergänzung - Skript </ref>
  
−
== Theory ==
+
=== Benchmark examples ===
 +
* simple cantilever under tip-load (moment and force) in a linear calculation including shear deformation: ..\examples\benchmark_examples\elements\beam1\cbm_beam1.dat
 +
* cantilever under various end-loads including shear deformation in a linear calculation: ..\examples\benchmark_examples\elements\beam1\cbm_beam1_stalin_timoshenko.dat
 +
* buckling analysis of a single-span column (Euler 2): ..\examples\benchmark_examples\elements\beam1\cbm_beam1_buckling.dat
 +
* using the ElementBeam1 as a design element starting with a quarter-circle: ..\examples\benchmark_examples\elements\beam1\cbm_beam1_design.dat
 +
* Theory of 2nd order under tension and compression: ..\examples\benchmark_examples\elements\beam_thII\cbm_Beam1_Th2O_1_Bsp_Skript_2.dat
 +
* spatial frame including local orientations THETA (see depicted above) in a linear computation under dead load: ..\examples\benchmark_examples\elements\beam1\cbm_beam1_stalin_deadload.dat
  
−
The theory and finite element formulation is described in detail in the work of Dieringer
+
== Theory ==
−
<ref name="Die09">Dieringer, F.: Implementierung eines geometrisch nichtlinearen Membranelements in einer objektorientierten Programmierumgebung, Masterthesis, Chair of structural analysis, Technische Universität München, 2009</ref> and Linhard
+
−
<ref name=Lin2009">Linhard, J.: Numerisch-mechanische Betrachtung des Entwurfsprozesses von Membrantragwerken, PhD-Thesis, Chair of structural analysis, Technische Universität München, 2009</ref>
+
−
 
+
−
For the correct use of the membrane element and the interpretation of related results, the following aspects should be considered:
+
−
 
+
−
 
+
−
=== Material parameter ===
+
−
With the parameter MAT the material, that would be used in the calculation, for the membrane element is defined. A very popular mistake is that a material number would be used, that isn't defined already. Please ensure that the material that you would like to use at this point are already exits. The following materials are testet for the membrane element:
+
−
* linear elastic isotropic
+
−
* linear elastic orthotropic (Münsch-Reinhardt)
+
−
* multilinear elastic isotropic
+
−
* elastoplastic isotropic
+
−
* material on the basis of response functions
+
−
 
+
−
=== Thickness parameter ===
+
−
The parameter THICKNESS defines the thickness of the membrane. The thickness should be constant over the element.
+
−
 
+
−
=== Prestress directions on the surface ===
+
−
The parameters ''A_X, A_Y, A_Z and B_X, B_Y, B_Z'' are used to define the prestress directions on the surface. In this approach the principle directions of the prestress are defined in a plane area (see figure below). The definition of the area is given by the two vectors '''f'''<sub>1</sub> and '''f'''<sub>2</sub>. The normal vector of the area can be calculated with the cross product of the in plane vectors '''f'''<sub>3</sub>='''f'''<sub>1</sub> x '''f'''<sub>2</sub>. Afterwards the line of intersection '''T'''<sub>1</sub> of the area which is given by '''f'''<sub>1</sub> and '''f'''<sub>3</sub> and the curved surface can be calculated. In this approach '''T'''<sub>1</sub> is interpreted as the first principle direction of the prestress on the curved surface. With the assumption that '''T'''<sub>3</sub> is equal to the surface normal vector '''G'''<sub>3</sub> (not uniformed), the second direction of the prestress is calculated as '''T'''<sub>2</sub>='''T'''<sub>1</sub> x '''T'''<sub>3</sub>. W.r.t. the parameters for the input file, only the plane area with the vectors '''f'''<sub>1</sub> and '''f'''<sub>2</sub> have to be defined. Referring to the depict approach the vector '''A''' defines the vector '''f'''<sub>1</sub> and the vector '''B''' defines the vector '''f'''<sub>2</sub>.
+
−
 
+
−
[[File:Prestress_Directions_for_Membranes.jpg|600px|up|Definition of the prestress direction for Membrane]]
+
−
 
+
−
=== Prestress state '''&sigma''' ===
+
−
SIG11, SIG22, SIG12 describes the prestress of the membrane element. The element is based on the plane stress assuption. Due to that only normal and shear stresses in the midplane have to be defined. SIGG11 is the stress acting in '''T'''<sub>1</sub>, SIG22 acting in '''T'''<sub>2</sub> and SIG12 is the in plane shear, whereas SIG12=SIG21 (see figure below).
+
−
 
+
−
[[File:Stress_state_for_membranes.jpg|600px|up|Stress state for Membranes]]
+
  
−
=== Lagrange type ===
+
The element implementation mainly follows the implementation of a linear 3D-beam element in
−
With the LARANGE parameter it is possible to switch between form finding and statical/dynamical analysis. For the value UPDATED the element is for form finding and for the value TOTAL the element is for statical/dynamical analysis. It is important that the LANGRANGE parameter match to the type of analysis.
+
FELyX <ref name="FELyX"> https://www.rdb.ethz.ch/projects/project.php?proj_id=8314 </ref>,
 +
Schwarz <ref name="Schwarz1991">Schwarz, H.: Methode der Finiten Elemente, Teubner, 1991</ref> and
 +
Wunderlich <ref name="Wunderlich">Wunderlich, W.: Statik der Stabtragwerke, Teubner, 2004</ref>.
  
 +
As it is based on the Hermite-form functions (for the linear element), a Bernoulli beam can be modelled by one single element.
  
 +
Theory of 2nd order has been implemented according to <ref name="Mehlhorn">von Mehlhorn, G.: Ingenieurbau - Grundwissen: Baustatik / Baudynamik, Ernst&Sohn, 1995</ref>, pp. 179/180.
  
 
== References ==
 
== References ==
  
 
<references/>
 
<references/>

Latest revision as of 07:41, 13 January 2017


Contents

General Description

Element Type

  • This beam element is a 2 node linear 3D-beam taking into account shear deformation (Timoshenko-beam element). For non-linear analyses the element is enriched by theory of 2nd order kinematics.
  • This beam element has 6 DOFs per node (three translations and three rotations).
  • The stiffness matrix for the linear calculation is hard-coded, thus not needing any integration. For theory of 2nd order, the normal force in the element leads to modifications in the stiffness matrix.

Degrees of Freedom

For the Beam1 element use the 3 translatoric degrees of freedom DISP_X, DISP_Y, DISP_Z and the 3 rotatoric degrees of freedom ROT_X, ROT_Y, ROT_Z.

Theory of 2nd Order

If Theory of 2nd Order should be taken into account, a nonlinear calculation (ANALYSIS STA_GEO_NLIN) with only one timestep has to be executed. The stiffness matrix is calculated with the accurate auxiliary values (“Strichwerte”) A’, B’ and D’ see [1]. In case of nonlinear calculation the shear correction factors are no longer considered.

Dynamic

Since a mass-matrix is implemented, the Beam1-element can also be used in dynamic analyses (including eigenfrequency,...) where it has already been successfully applied.

Orientation of the local coordinate system

The Beam1 element uses the following definition for the determination of the local coordinate system (needed for the orientation of IYY and IZZ,...):

  • the local x-axis is oriented from node 1 to node 2 of the beam
  • the local y-axis lies in the global XY-plane, such that the local z-axis points in the same half-space as the global Z-axis (mathematically spoken: the local z-axis and the global Z-axis result in a positive dot-product)
  • the local z-axis is perpendicular to the other two local axis, following the right-hand-rule for x-y-z
  • exception: If the local x-axis (i.e. the beam axis) points in the direction of global Z, the local y-axis points in the direction of the global Y-axis. The local z-axis once again follows the right-hand-rule for x-y-z.

In case that a rotation of the local coordinate system is needed (rotated elements, inverse definition of IYY and IZZ,...) an angle THETA has to be specified. This angle rotates the whole coordinate system around the local x-axis, following the right-thumb rule (i.e. the thumb of the right hand points in the direction of the local x-axis).

Orientation of the resultant forces

The Beam1 element has 6 resultant forces in accordance with the degrees of freedom. The resultant forces, [ N V1 V2 | MT M1 M2 ], are oriented along the local axes on the positive section of the beam. Note that the resultant forces are evaluated in the center of the beam element, so it's the mean value of the two ends. For the orientation, cf. also the orientation sketch:

Resultant forces orientation for element Beam1

Input Parameters

Parameter Description

Compulsory Parameters
Parameter Values, Default(*) Description
MAT EL-MAT int Number for the used Material

e.g. MAT=EL-MAT 1

AREA Definition of the cross-sectional area of the beam
IYY, IZZ Definition of the moments of inertia
Optional Parameters
KY, KZ 0 Shear correction factor; if 0 or no value specified, shear is not taken into account (Bernouolli-beam theory);
Note: For Theory of 2nd Order, Bernoulli-beam theory is assumed.
THETA 0 Angle of rotation of the local coordinate system around the beam axis in degrees

Example of a Complete Input Block 

EL-PROP 1 : BEAM1
MAT= EL-MAT 1
AREA=5.555  IYY=1.222  IZZ=1.333
KY=1.4   KZ=1.5
THETA=90

Use of the shear correction factors KY and KZ

The shear correction factors KY and KZ depend on the cross section of the beam. For a rectangle, KY resp. KZ are usually considered equal to 1.2, which gives a factor of α=1/Ki=5/6.

Use of the rotation parameter THETA

The rotation parameter THETA and its use is explained in the section concerning the coordinate system above.

The torsional resistance IT

The torsional resistance IT is interpreted as the polar moment Ipp, i.e.: IT = Ipp = IYY + IZZ.

Element Loading

For the moment, only nodal forces in the three global directions can be applied (i.e. Fx, Fy, Fz). Being a line element not all general load cases are applicable.

Dead Load

  • implemented

Tests and Benchmarks

Static linear analysis

Static test for element Beam1

For the moment, the element Beam1 has successfully been tested in 3D in all its linear static features, including

  • bending, axial deformation, torsion,
  • shear deformation (separately definable for both local axes),
  • rotation around the local axis.

As an example, the structure on the right was part of the final tests.

Theory of 2nd order

Test herefore is a clamped frame with one pillar under compression and the other under tension cp. "Statik Ergänzung - Skript" [1]

Benchmark examples

  • simple cantilever under tip-load (moment and force) in a linear calculation including shear deformation: ..\examples\benchmark_examples\elements\beam1\cbm_beam1.dat
  • cantilever under various end-loads including shear deformation in a linear calculation: ..\examples\benchmark_examples\elements\beam1\cbm_beam1_stalin_timoshenko.dat
  • buckling analysis of a single-span column (Euler 2): ..\examples\benchmark_examples\elements\beam1\cbm_beam1_buckling.dat
  • using the ElementBeam1 as a design element starting with a quarter-circle: ..\examples\benchmark_examples\elements\beam1\cbm_beam1_design.dat
  • Theory of 2nd order under tension and compression: ..\examples\benchmark_examples\elements\beam_thII\cbm_Beam1_Th2O_1_Bsp_Skript_2.dat
  • spatial frame including local orientations THETA (see depicted above) in a linear computation under dead load: ..\examples\benchmark_examples\elements\beam1\cbm_beam1_stalin_deadload.dat

Theory

The element implementation mainly follows the implementation of a linear 3D-beam element in FELyX [2], Schwarz [3] and Wunderlich [4].

As it is based on the Hermite-form functions (for the linear element), a Bernoulli beam can be modelled by one single element.

Theory of 2nd order has been implemented according to [5], pp. 179/180.

References

  1. ↑ 1.0 1.1 Bletzinger, K.-U.: Statik Ergänzung - Skript
  2. ↑ https://www.rdb.ethz.ch/projects/project.php?proj_id=8314
  3. ↑ Schwarz, H.: Methode der Finiten Elemente, Teubner, 1991
  4. ↑ Wunderlich, W.: Statik der Stabtragwerke, Teubner, 2004
  5. ↑ von Mehlhorn, G.: Ingenieurbau - Grundwissen: Baustatik / Baudynamik, Ernst&Sohn, 1995




Whos here now:   Members 0   Guests 0   Bots & Crawlers 1
 
Retrieved from "http://carat.st.bv.tum.de/caratuserswiki/index.php/Users:General_FEM_Analysis/Elements_Reference/Beam1"
Personal tools
Content for Users
Content for Developers